Saturation Rank for a Classof Non-reductive Lie Algebras

PAN Yang, YE Chang

(1.School of Artificial Intelligence and Big Data, Hefei University, Hefei 230601, China;2.School of Science, Huzhou University, Huzhou 313000, China)

Abstract：In this article, we investigate the saturation rank of a class of non-reductive Lie algebras, defined over an algebraically closed field k of positive characteristic p. More precisely, if pJ is a standard parabolic subalgebra of sln+1and uJis the corresponding nilradical, we show that the saturation rank of uJ equals the semisimple rank of the algebraic k-group SLn+1(k) when |J|=1 and p≥n+1.

Keywords：saturation rank; parabolic subalgebras; richardson element

0 Introduction

Let k be an algebraically closed field of positive characteristicp, and (g,[p]) be a finite dimensional restricted Lie algebra over k. We consider the saturation rank srk (g), which is an important invariant of restricted Lie algebras[1]. A prototypical case occurs when g is the algebraic Lie algebras of reductive algebraic groupsG, which implies that srk (g)=rkss(G) is the semisimple rank of a reductive algebraic group under some mild restrictions[2].

The saturation rank srk (g), defined through the theory ofp-points expounded by Friedlander and Pevtsova in their paper [3], plays an important role in the representation theory of g. In terms of finite groups, it is a basic method in the modular representation theory to restrict modules to elementary abelianp-subgroups. Likewise, for a restricted Lie algebra g, when restricting a g-module to elementary abelian subalgebra of a certain rank, one has to make sure that one does not lose any information in comparison with its restricted nullconeV(g). This is the point where the saturation rank enters the stage. As was shown in [4], the Carlson moduleLζis indecomposable, provided srk (g)≥2. In this paper, we investigate whether there is an affirmative answer to the question of determining srk (g) when g is non-reductive.

This question can be made much more precise by looking at the saturation rank of a certain class of subalgebras of general linear Lie algebras. LetG=SLn+1be the special linear algebraic group over k, and let g=sln+1be its Lie algebra. Given a standard parabolic subgroupPofG, we consider its unipotent radicalU. We denote p=Lie(P) and u=Lie(U)as the Lie algebras ofPandU, respectively. The adjoint action ofPon u affords an open orbit, known as the Richardson orbit, in which elements are called Richardson elements. As we show in Lemma 2, they do play a similar role as regular nilpotent elements did for reductive Lie algebras when concerning the problem of finding saturation rank.

Our paper can be divided roughly into two parts. We first in Section 1 recall the general facts of saturation rank of a restricted Lie algebra. Then we study standard parabolic subalgebras of sln+1by using the dimension vectord, which is verified in Lemma 1. For a dimension vectord, according to Theorem 1, it corresponds to a Richardson elementX(d). The construction ofX(d) is explicitly shown in [5] and [6], whereGis of classical type and the characteristic char(k)≠2. In our case, i.e.G=SLn+1, the Richardson elements can be read off from a labeled horizontal line diagramLh(d) Afterwards, in Section 2 we make progress in determining the centralizer ofX(d) in uJwhen |J| equals one. The terminology we use for Theorem 2 is the labeledk-chain taken from a labeled horizontal line diagram. By the proof of Lemma 2, up to conjugacy byPJ, we need to consider the local saturation rank ofX(d). Following the technical preparation worked before, we illustrate in Theorem 3 how labeledk-chain may be employed to study the local saturation rank of the Richardson element.

1 Preliminaries

1.1 Saturation rank

Let (g,[p]) be a finite dimensional restricted Lie algebra andrbe a positive integer. Recall that the restricted nullcone

V(g):={x∈g|x[p]=0}

is defined to be the fiber of zero of the map [p]:g→g. More generally, one can consider the variety

E(r,g):={e∈Grr(g)|[e,e]=0,e⊂V(g)}

for everyr≥1 where Grr(g) is the Grassmannian ofr-planes in g[7]. We consider a subsetVE(r,g)ofV(g) which is the union of all elements of E(r,g); that is,

Observe that ifr=1, then the equalityV(g) =VE(r,g)holds, leading to the following definition:

Definition 1[2]Let (g,[p]) be a finite dimensional restricted Lie algebra. Then the number

srk(g):=max{r∈N|V(g)=VE(r,g)}

is referred to as the saturation rank of g.

We choose an elementxofV(g). For anyr, we define the set

E(r,g)x:={e∈E(r,g)|x∈e}

to be the subset ofE(r,g) whose elements containx. We naturally associate to eachxof g the number

called the local saturation rank ofx.

1.2 Parabolic subgroups

We assume thatG=SLn+1is the special linear algebraic group over k with its Lie algebra g=sln+1. LetPbe a parabolic subgroup ofG, and letT⊆Pbe a maximal torus ofG. LetLbe the Levi factor ofPcontainingT, and letUpbe the unipotent radical ofP. LetBbe a Borel subgroup ofGcontained inPand containingT.

We write Φ for the root system ofGwith respect toT. Let Φ+be system of positive roots determined byB, and let Π={α1,α2,…,αn} be the corresponding set of simple roots. We say that a subgroupHofGis a standard Levi subgroup ifHis the Levi factor containingTof a parabolic subgroup containingB. In particular,Lis a standard Levi subgroup ofG.

LetJbe a subset of {1,2,…,n}, and ΦJbe the closed subsystem of Φ generated byαifori∈J. The subsetsJgive all standard parabolic subgroups ofG, namely

P=PJ=〈T,Uα|α∈Φ+∪ΦJ〉,

whereUαare root groups. Levi subgroups ofPJare then

L=LJ=〈T,Uα|α∈ΦJ〉.

1.3 Dimension vector

Notation 1Let lJbe a standard Levi subalgebra of sln+1. It has the shape of a sequence of square matrices (blocks) on the diagonal and zeroes outside. We use

d= (d1,d2,…,dr)

to denote the dimension vector of these block lengths.

Recall that a standard parabolic subalgebra of sln+1is uniquely determined by the dimension vector of its Levi factor. The following Lemma illustrates the fact and should be well-known, so we exclude the proof.

Lemma 1Suppose pJ⊆sln+1is a standard parabolic subalgebra defined via

J={1,2,…,n}r1,r2,…,rs},

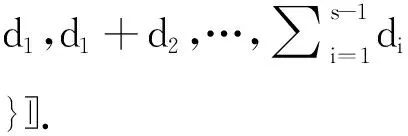
Henceforth, we may write p(d) instead of pJwhen it is necessary according to Lemma 1. Thanks to a fundamental theorem of Richardson,PJacts on uJwith an open dense orbitO; this orbit is called the Richardson orbit and its elements are called Richardson elements. Recently Baur[5]gave constructions of Richardson elements in the case k=C and later on she and Goodwin in their work[6] stated that these constructions remain valid for any algebraically closed field k of char(k)≠2.

1.4 Richardson elements

We now recall her constructions. Letd=(d1,d2,…,ds) be a dimension vector. Arrange s columns ofdidots, top-adjusted. A line diagram ford, denoted byL(d), is a collection of lines joining vertices of different columns such that each vertex is connected to at most one vertex of a column left of it and to at most one vertex of a column right of it and such that it cannot be extended by any line. We say that it is a horizontal line diagram if all edges are horizontal lines. Such a diagram will be denoted byLh(d). We label its vertices column wise by the numbers 1, 2, …,n+1, starting with column 1, labeling top-down. The labeled horizontal line diagram defines a nilpotent element

of p(d), whereEi,jis an elementary matrix of sln+1given by a line fromitoj.

Theorem 1[5]The mappingd→X(d) associates to each dimension vectorda Richardson element for the corresponding parabolic subalgebra p=p(d) of sln+1.

Example 1We chooseJ=∅ as an empty set. Then pJis a standard Borel subalgebra. By Lemma 1, we have

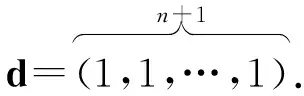
The labeled horizontal line diagramLh(d) is then

1—2—……—n+1，

by Theorem 1X(d)=E1,2+E2,3+…+En,n+1is a Richardson element of p(d).

i1—i2—……—ik+1.

Notation 2Given a dimension vectord. Define

2 Main result

ProofWe consider the set

We put

In view ofp≥n+1 and [2], we have

Theorem 2Let p(d)⊆sln+1(k) be given byJ= {r}, 1≤r≤n. Then the centralizer z(d) of the Richardson elementX(d) in the nilradical uJis spanned by the generators of all Rktogether with one choice of elementary matrix(es) from the set {E1,r+1,Er+1,n+1}depending on r.

1—……—r—r+2—……—n+1
r+1

Reading off the Richardson element associated to p(d), we get

Observe that

is a bijective map. With this map, we are ready to characterize the elements of z(d). Notice that any nilpotent element in uJis given by the form

giving

Assume that [X(d),X]=0. Direct computation yields the following relations:

(b)ai,r+1=0 for 1

(c)a1,r+1,ar+1,n+1, anda1,n+1are arbitrary.

Through these relations, we conclude that the elementXis a linear combination of generators of Rk(1≤k

IfJ={1} orJ={n}, then

The determination of elements of z(d) for these two cases is similar to the case when 1

Example 2Let p(d) be a standard parabolic subalgebra of sl4(k) given byJ={1}. Thend=(2,1,1), andX(d)=E13+E14. In the labeled horizontal line diagramLh(d)

1—3—4
2

we have R1=k(E13+E34), R2=kE14. By Theorem 2, the centralizer ofX(d) in uJis z(d)=[E13+E34,E14,E24].

Theorem 3LetPJ⊆SLn+1(k)(n≥2) be a standard parabolic subgroup with unipotent radicalUJgiven byJ={r}. We write pJand Lie(PJ). Ifp≥n+1, then the following statements hold:

(1)The saturation rank srk(uJ) isn.

(2)Any maximal elementary subalgebra associated to a Richardson elementX(d) is unique or determined by (a:b)∈P1.

(3)The variety E(n,uJ)X(d)is irreducible of dimension ≤1.

RemarkThe following proof only concerns the case when 1

ProofWe prove the following statement by induction: any elementary subalgebra associated to a Richardson element in uJof sln+1(k) has dimension at most n and any subalgebra of this dimension is of the form R1⊕…⊕Rn-1⊕k(aE1,r+1+bEr+1,n+1) parametrized by points (a:b)∈P1. This ultimately implies claims (1), (2) and (3).

We consider the following extension

Note that uJ/e2≃u′Jis the nilradical of p′J, where p′Jis the standard parabolic subalgebra of sln+1(k) given byJ={r}. The corresponding dimension vector of p′Jis then

According to this we have

pr(X(d))=X(d′)，

Now we assume thate1has the maximal dimensionn. We denote by R′ithe one dimensional vector space defined in Definition 2 for the dimension vectord′ in case of sln(k). As discussed above, if kE1,r+1is a direct summand ofpr(e1), the maximal dimension is attained if and only if dimpr(e1)=n-1, and by induction we have

pr(e1)=R′1⊕…⊕R′n-2⊕kE1,r+1.

Alternatively, for the dimension to be maximal we need dimpr(e1)=n-2, and by Theorem 2 we have

Sincee1∩e2⊆z(d)∩e2, the pre-image of R′i(resp. kE1,r+1) is Ri+kE1,n+1+kEr+1,n+1(resp. kE1,r+1+kEr+1,n+1+kE1,n+1) by Theorem 2 for 1≤i≤n-2. Note thatE1,n+1can commute with any elements ine1and kE1,n+1=Rn-1, whence

e1=R1⊕…⊕Rn-1⊕k(E1,r+1+cEr+1,n+1),c∈k

ifpr(e1)=R′1⊕…⊕R′n-2⊕kE1,r+1, and

e1=R1⊕…⊕Rn-1⊕kEr+1,n+1

ifpr(e1)=R′1⊕…⊕R′n-2. This finishes the proof of our claims.