改进的自适应复制、交叉和突变遗传算法
陈 琳,王子微,莫玉良,潘海鸿
(广西大学机械工程学院,广西 南宁 530004)
1 引言
在工程实践中,函数优化及组合优化等问题需要在复杂的搜索空间中寻找最优解,但随着问题规模的扩大以及约束条件的增多,常引发组合爆炸。多种优化算法种遗传算法在实际大规模系统应用中具有强稳健性,对函数依赖程度低等优点[1-3]。它是一种利用自然选择和生物进化思想在搜索空间中搜索最优解的随机搜索算法。然而在传统遗传算法中,遗传算子通常人为预先设置。且在解决复杂的多极值函数问题上需要数千次的遗传迭代才可寻得最优解,故很多学者致力于改善进化过程,提出自适应遗传算法以提升算法效率[4-5]。
自适应遗传算法在收敛速度加快的同时却引发早熟现象。为此,王悦等[6]提出使用实数编码、线性排序的适应度分配方法、实值变异和基于适应度的线性笔记的改进交叉策略,通过实验验证了该算法收敛最为平稳。Tarek等[7]提出将局部搜索引入到遗传算法中来创建混合算法,通过实验验证该算法可以自适应学习并提高搜索全局最优解的能力。杨从锐等[8]提出交叉突变调整新标准,将平均适应度和最优适应度比值的反正弦作为参考因素,将π/6作为参考阈值,通过判断新增参考因素与阈值的大小关系并以此对交叉率及突变率进行调整。Wang等[9]提出一种改进的NSGA2算法用于解决多目标问题。NSGA2算法每次迭代计算后,在Pareto最优集上执行一种局部搜索策略以搜索更好的解,从而使NSGA2算法获得更好的局部搜索能力。这些学者主要是在进化过程中根据进化的不同阶段改进建立相应的交叉概率及变异概率。这在一定程度上能够改善算法的搜索能力,但因引入诸多人为经验参数,导致测试结果不稳定。
针对该问题,提出一种改进的自适应复制、交叉和突变遗传算法。该自适应遗传算法中的复制率、交叉率和突变率可根据种群规模、种群中个体的分布情况和遗传迭代不同阶段进行自适应变化,进而克服过早收敛陷入局部最优解,并提高搜索精度。
2 自适应遗传算法遗传算子设计
自适应遗传算法的交叉率和突变率改进:
1)交叉率的改进:如交叉两个体中的较大适应度与种群最大适应度之差较大时,视为该交叉个体为非优质个体,需适当增加其交叉率,使其交叉获得优质样本的概率提升;如种群最佳适应度与平均适应度之差较大时,视为样本较为分散(意味着适应度函数尚未进入极值),需适当下降其交叉率使分散的种群尽快迭代;在交叉个体间的较优适应度值小于种群平均适应度时,样本视为较劣样本,为减少计算量,较劣样本的交叉率将不再依据种群分布加以考虑并设置为恒定值。故将交叉率改进为
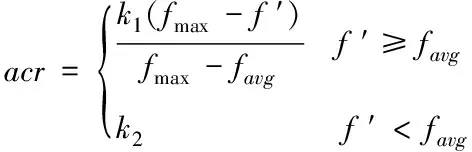
(1)
式中fmax为种群中个体最大适应度值,f′为两个要交叉个体中适应度值较大个体的适应度值,favg为种群中所有个体的平均适应度值,k1,k2为0到1之间的数,通常人为设置。
2)突变率的改进:与交叉率类似,需考虑调整要突变个体与平均适应度差值,故将突变率改进为
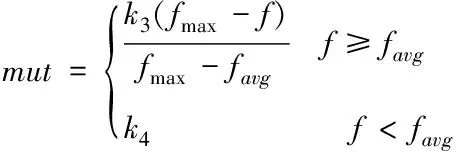
(2)
式中f为要突变个体的适应度值,k3,k4为0到1之间的数,通常人为设置。
遗传算法收敛性的测试用F7函数
f(x,y)=(x2+y2)0.25[sin2(50(x2+y2)0.1)+1.0]
(3)
该函数有无数个局部极值点,其中只有(0,0)为全局最小值点,最小值为0。适应度收敛值误差小于0.1即视为收敛至全局最优解。
收敛性的仿真测试参数设置:k1=0.25,k2=0.25,k3=0.35,k4=0.35,x取值范围为(-6,6),y取值范围为(-6,6),复制率为dup=0.2,样本数N为500,遗传迭代代数为100。
F7函数适应度遗传迭代结果图1中发现,其在迭代收敛速度上有较大的提升,但随着收敛速度的提升出现早熟现象。为避免实验结果的偶然性,对样本进行20次重复测试迭代,仿真结果有15次函数陷入局部最优解,其适应度收敛值在0.5-1.5间波动,并且无法跳出获得最优解。
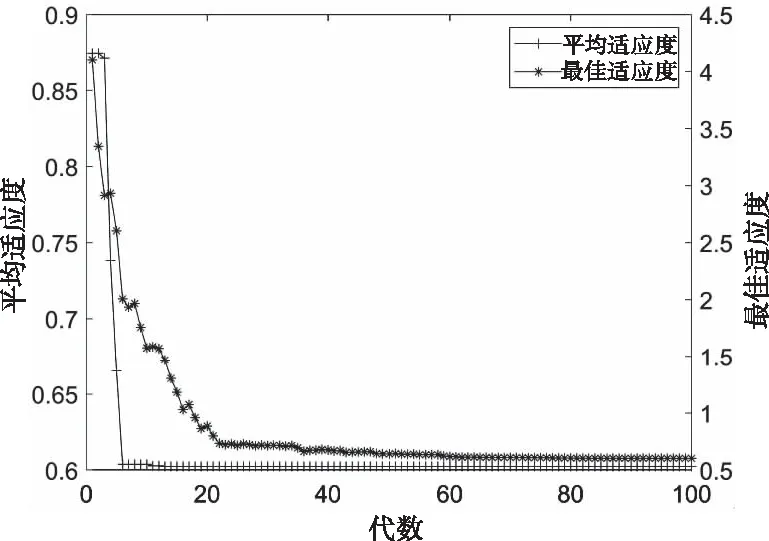
图1 F7函数适应度遗传迭代图
表明自适应遗传算法中对于交叉率和突变率的改进在解决复杂多极值问题上仍存在易陷入局部最优解的问题。
3 改进的自适应复制、交叉和突变遗传算法
产生上述问题的可能原因分析:
1)交叉率和突变率算子的设计未考虑样本总数N。样本量越大意味着样本内容越丰富,适应度值覆盖域越广。而对于越丰富的样本,一个较大的交叉和突变率意味着其造成的波动越大,使种群收敛减缓。
2)遗传算子设计未考虑种群中个体的分布情况。图2中d为中间区域样本数量M与样本总数N之比,当d数值较小时,则样本中间区域中个体分布较少,说明它们不是一个稳定集中的群体,所以交叉和突变的概率需要减小。
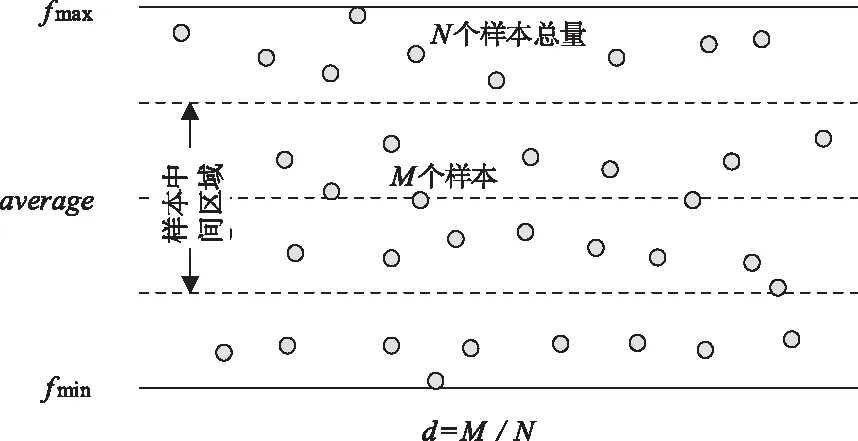
图2 种群中个体分布情况图
3)迭代中复制率是定值。遗传迭代中样本分布范围越大,即意味着样本优劣并存,此时需一个较大复制率以淘汰种群中的劣质样本;而随着迭代进行,样本高度集中时,为避免陷入局部最优,需保留部分分散的样本为样本交叉提供引入优质解的机会。
4)人为经验对交叉率和突变率算子中k1、k2、k3、k4取值,这需大量重复实验测试才能得出最合适值,导致计算量大。
为此,提出一种改进的自适应复制、交叉和突变遗传算法:
1)复制率的调整:自适应遗传算法中将复制率设置为定值,在样本数较少时其影响不大,而在大样本及多维空间迭代时,对于样本总体而言,当样本适应度分散时,较劣适应度突出明显,需快速去除样本中较劣样本;当适应度集中时,平均适应度向最佳适应度靠拢,复制率应随之下降。
复制率算子设计中首先需考虑样本最优适应度与平均适应度的差值。当样本最优适应度与平均适应度越大时,则样本分布所跨区域越大,复制率应增大以淘汰较劣样本;当中间区域的样本分布越少(即d越小),则样本越分散,复制率也应增大。复制率设计为
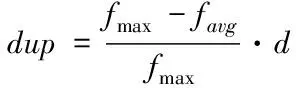
(4)
式中,fmax表示种群中个体适应度的最大值,越高的最大适应度值意味着种群样本中所保存的样本最优性好,复制率会随之降低;d表示样本集中程度,越集中的样本意味种群适应度收敛程度越高,复制率亦会随之上升,加快整个种群收敛速度。(fmax-favg)表示种群中个体最大适应度值和种群中所有个体的平均适应度值之差,该项表示整个种群适应度的离散程度,两者之差越大即表示种群分布越离散,故复制率也随之增大。
2)交叉率的调整:在多极值问题上,需使用较多的样本数,通常种群适应度丰富度与样本数成正相关,愈多的样本意味着更高的样本丰富度。对于越丰富的种群样本,其拥有优质样本的概率则越高,较大的交叉率会导致种群内样本交叉产生劣质样本的概率将大于产生优质样本的概率。故初始交叉率应适当下降,以避免不必要的较劣样本引入和波动。
在遗传迭代中,随着遗传迭代次数t的增加,遗传可分为前期和后期。遗传前期样本混杂,需尽快找出较优解;而遗传后期样本平均适应度已高度靠近最佳适应度,较大的交叉率反而会带来不必要的波动。当个体适应度较为集中或较为分散时,视为样本进入高度集中或高度分散两种极端情况,此时应需适当调整交叉率。为此,将交叉率改进为
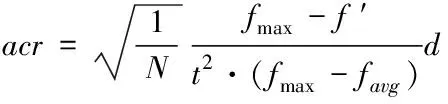
(5)
式中,t为迭代次数,随着迭代进行种群已逐渐向种群中最优适应度靠拢,交叉率将随迭代而逐渐减小。分子(fmax-f′)表示种群中个体最大适应度值和两个要交叉个体中适应度值较大个体的适应度值之差,该项表示交叉个体在种群中的离散程度,两者之差越大即表示要交叉的两个体的适应度值越低,交叉率需随之增大,增加引入优质样本的概率;(fmax-favg)表示种群中个体最大适应度值和种群中所有个体的平均适应度值之差,其与(fmax-f′)的比值表示交叉两个体适应度与种群平均适应度的差距,差值越大时意味着该两个体越接近边界位置,为增加引入优质样本的概率,故交叉率随之增大;越大的种群个数N意味着越丰富的种群适应度,即有越大的可能含有优质解,故交叉率会随之种群数N增大而减小;样本集中程度d变大意味种群适应度收敛程度变高,交叉率会随之上升增加引入优质解的概率。
3)突变率的调整:自适应遗传算法突变率设置初始值较大且下降幅度较小,对于多极值函数而言,其样本丰富度与其样本数量成正比,故突变率取值应与样本总数N相关,对于越大的样本总数意味着样本中含有越详细的总体特征。较大的突变率会导致样本中波动增加,故突变率应与样本总数成负相关,以避免过高的突变率导致的适应度函数不必要波动。
随着遗传迭代次数t的增加,较大的突变率所引入的新的样本的波动会影响遗传算法的收敛性,故突变率应随迭代次数增加应适当改变。当个体适应度较为集中时,往往意味着平均适应度函数逼近一个极值,但无法确定其是否为最优解,需对突变率进行适当调整,使其不易陷入局部最优解。因此,将突变率改进为
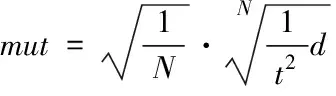
(6)
与交叉率算子设计相类似,综合考虑种群个数、样本集中程度和迭代次数变化的影响,突变率随着N的增大而减小,随着d的增加而增加,随着迭代次数t的增加而逐渐减小。
遗传算子验证:在遗传算法中,由于个体每次交叉突变均只和当前状态相关,与前期状态无关,故采用马尔科夫链序列来构造种群的适应度变化。根据马尔科夫链序列的收敛条件对改进的自适应复制、交叉和突变遗传算法中的遗传算子进行验证
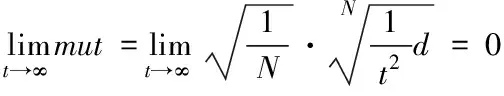
(7)
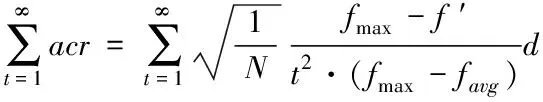
(8)
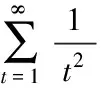
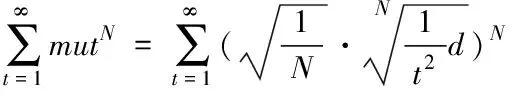
(9)
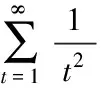
改进的自适应复制、交叉和突变遗传算法中遗传算子满足使算法收敛的条件,使得该算法在理论上可收敛,求出全局最优解(图3)。
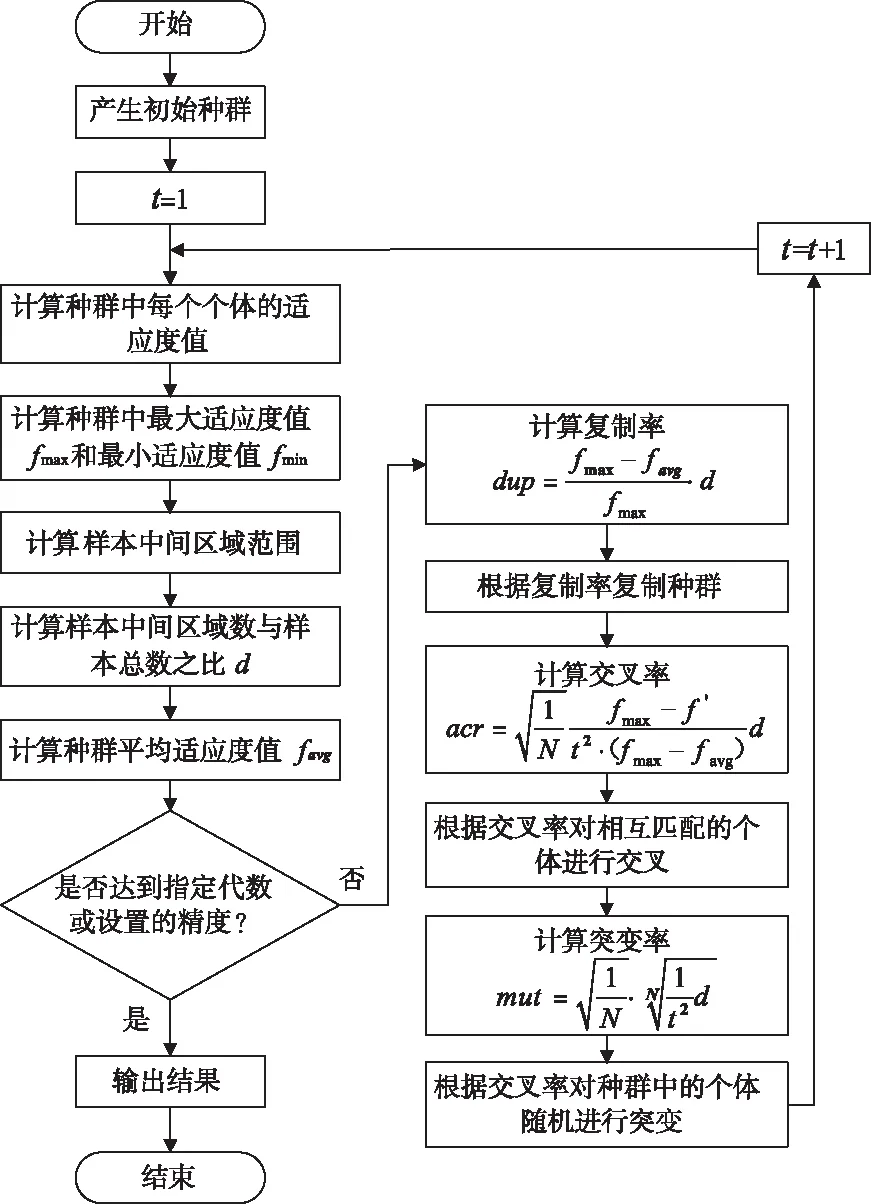
图3 改进的自适应复制、交叉和突变遗传算法流程图
4 仿真分析
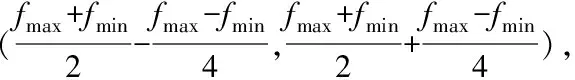
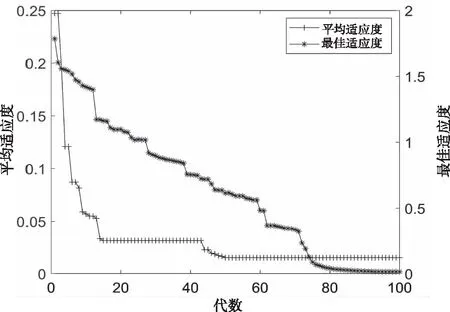
图4 F7函数适应度遗传迭代图
图4为F7函数适应度遗传迭代图,图4中平均适应度变化可看出,迭代50次后平均适应度收敛已经到达全局最优解,其值为0.03074;迭代95次后,最佳适应度值保持不变。
图5和图6分别为自适应遗传算法和改进的自适应复制、交叉和突变遗传算法适应度全局搜索结果。图5中可知,自适应遗传算法搜索出的适应度为0.6053,陷入局部最优且距最小值相差较大。图6中,改进的自适应复制、交叉和突变遗传算法搜索的适应度值为0.03074,小于设定的阈值0.1。显然改进后的算法全局搜索能力更强,结果更精确。
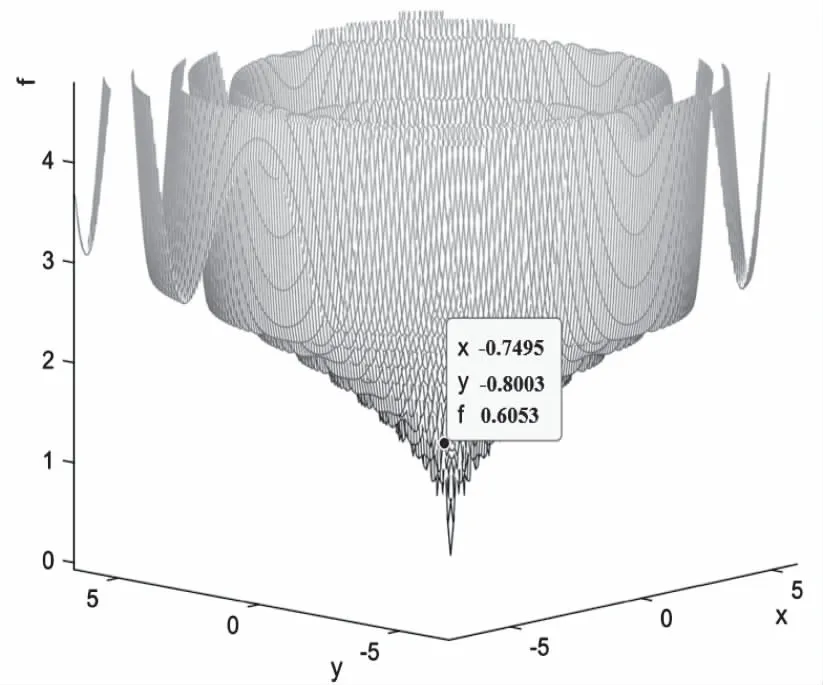
图5 自适应遗传算法适应度搜索结果
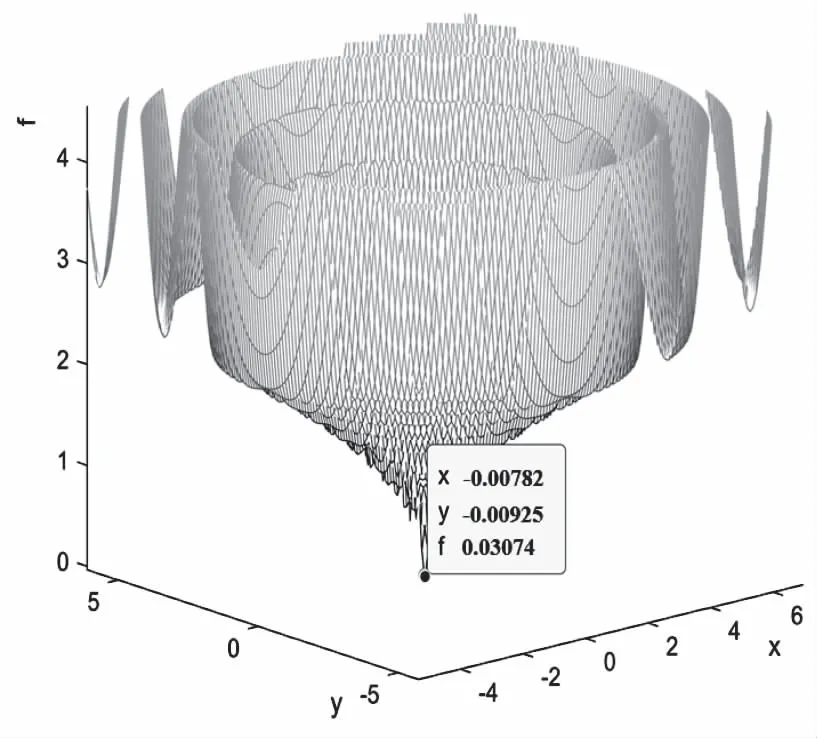
图6 改进的自适应复制、交叉和突变遗传算法适应度搜索结果
为避免保证实验结果偶然性,分别用自适应遗传算法和改进的自适应复制、交叉和突变遗传算法进行50次重复实验,结果见表1。
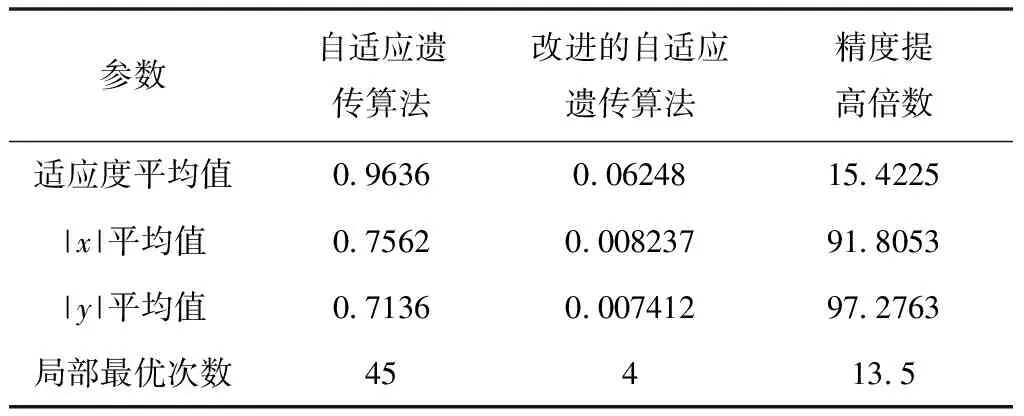
表1 2种遗传算法搜索值
由表1可知,改进的自适应复制、交叉和突变遗传算法相比于自适应遗传算法在适应度的搜索精度上提升了15.4225倍,并且陷入局部最优的次数下降了13.5倍。
5 结论
为解决自适应遗传算法中常出现易陷入局部最优解的问题,同时针对更加复杂且极值更多的适应度函数,提出遗传因子改进方案,并理论证明其收敛性。通过F7函数对改进的自适应复制、交叉和突变遗传算法进行收敛性验证。实验结果表明该算法收敛速度快且精度高,同时不易陷入局部最优解也证明改进的自适应复制、交叉和突变遗传算法在解决早熟问题上的可行性。

