行星际飞行仿真视点运动控制算法设计
葛双全,孟德壮
(中国工程物理研究院计算机应用研究所,四川 绵阳 621900)
1 引言
地球外层空间环境的特殊性是人类从事空间活动和认知空间环境变化规律的主要障碍,可视化仿真技术的发展为改变这一状况提供了契机。可视化仿真技术采用图形或图像的方式实现空间和时间数据的视觉化,将可视化仿真技术应用于空间科学研究与工程实施领域,一方面能够通过可视化的形式表示空间环境,直观展现其分布状况、运行规律及动态特性,另一方面可仿真空间科学研究活动,为空间科学研究提供支持[1]。
行星际空间环境可视化需求多样,既有厘米级的飞行器载荷高精度动作仿真,也有星际飞行运动仿真。根据不同的空间仿真设计,观察者在同一虚拟场景内既可能需要观测仿真对象相对位置关系,又要清晰地观察飞行器载荷动作行为。因此,设计适用于满足视点在大尺度星际空间快速运动条件下的控制算法具有重要意义。
2 行星际飞行仿真特征分析
2.1 空间尺度大
行星际飞行仿真的大尺度包含两方面含义:太阳系距离尺度变化巨大;仿真对象模型本身尺度变化巨大。对于前者而言,水星是离太阳最近的行星,其距离太阳约为5791万千米,海王星是离太阳最远的行星,其距离太阳约为45亿千米,飞行器载荷动作则为分米级或厘米级。对于后者而言,太阳直径约为70万千米,而飞行器大小通常只有数米,各仿真对象模型大小存在很大的数量级差。
2.2 空间关系复杂
行星际飞行仿真研究对象包括空间环境、行星及其卫星、飞行器及其载荷等,各仿真对象空间关系复杂。太阳对飞行器和行星的光照、飞行器对地覆盖等计算都受制于仿真对象之间的相对位置关系,而针对各仿真对象相对位置关系的描述基于统一的空间坐标体系,如行星运动仿真通常在日心黄道坐标系下描述各行星的运动轨迹;飞行器运动仿真通常在该飞行器所属行星的惯性坐标系下描述该飞行器运动;发射飞行器通常在地球固定坐标系下描述其发射活动;描述飞行器及其载荷则通常采用轨道坐标系及飞行器本体坐标系。
2.3 感知效果差
相对于行星之间的距离,行星本身尺度可以忽略不计,太阳系内部空间基本可认为空无一物。在行星际飞行仿真场景中,当希望观测星际运动轨迹时,就不得不将视点置于离太阳很远的位置。当希望了解飞行器状态时,又必须将视点移动到飞行器本身或其附近。另外,在如此浩瀚的空间范围内,由于缺乏参展物,观察者将难以根据周围环境判断视点所处的空间位置,从整体上感知仿真对象的分布情况。
3 视点运动控制算法设计
3.1 空间坐标体系构建
空间坐标体系用于描述仿真对象在太阳系空间的位置关系,是行星际飞行仿真系统的运行基础。从空间环境要素分析来看,对地球空间环境的研究几乎都是以地球为中心来研究空间环境对人类生产活动的影响。但由于星际飞行涉及大量的行星间相对位置关系、飞行器及其载荷与行星(主要是太阳和地球)的相对位置关系等,因此构建行星际飞行仿真坐标系统必须以日心黄道坐标系统为基准。考虑到行星际飞行仿真所涉及的各种试验场景和仿真对象,坐标系统包括飞行器轨道坐标系、本体坐标系、地球固定坐标系、发射场坐标系、地球惯性坐标系、地球黄道坐标系、日心黄道坐标系、太阳惯性坐标系、太阳固定坐标系等[2-4]。图1所示为行星际飞行仿真坐标体系。
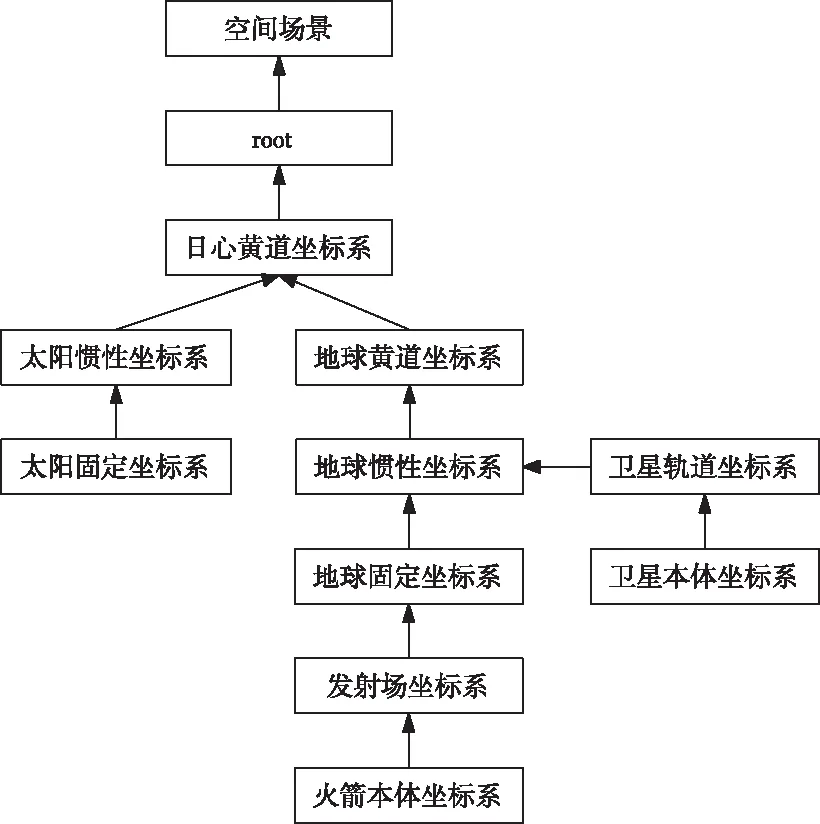
图1 行星际飞行仿真坐标体系
3.2 视点控制机制
视点是观察者查看虚拟场景的接口,OpenGL将视点抽象为观察者,观察者将许多模拟的元素聚合在一起观测。每个观察者都有各自关联的场景、通道和环境。
观察者也是场景中的活动物体,所以它也有移动、旋转等改变位置的操作,观察者可以挂接到任一场景节点下。由于坐标变换矩阵的累加性,观察者的直接父节点和间接父节点的改变都会对观察者的位置产生影响。观察者坐标定义采用右手坐标系,视点位于坐标的原点,视点正前方为正Y轴,X轴正方向朝右,Z轴正朝上。通过控制观察者所处的坐标空间和观察者的位置和姿态,就可以决定空间仿真场景提供给观察者的视觉信息。
3.3 视点运动控制算法设计
3.3.1 从三维空间到二维屏幕
渲染管道用于描述OpenGL一系列绘制过程[5-6],是三维空间对象从世界坐标系到屏幕坐标系的基本流程,即从三维空间到二维屏幕,其渲染流程如图2所示。
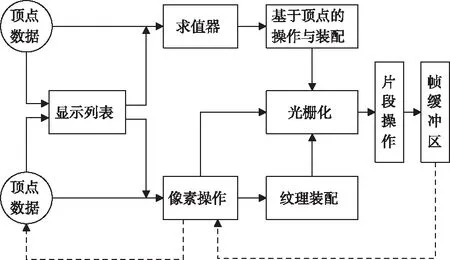
图2 OpenGl渲染管线
顶点数据通常是指三维空间中的物体的坐标、法线向量等,这些数据可以保存在显示列表中,也可以直接进行处理。求值器根据顶点数据计算表面法线、纹理坐标、颜色以及空间坐标值,基于顶点的操作首先对单个顶点进行操作,然后把顶点装配成为图元。像素操作将内存中的像素数据转换成图形硬件支持的数据格式,如果像素数据是从帧缓冲区中读取的,就对其进行缩放、平移、映射和截取。经过处理后的顶点数据和像素数据通过光栅化转换为片段,片段对应于帧缓冲区中的一个像素,具有各自的演示和深度值。对这些片段进行颜色计算、纹理应用、片段测试等,最后,片段会被绘制到适当的缓冲区,显示设备从缓冲区读取数据并显示到屏幕上。
3.3.2 算法描述
3.3.2.1 问题描述
行星际飞行仿真需要考虑空间环境整体比例缩放、行星比例缩放、飞行器比例缩放、轨道高度自定义、飞行器轴向运动比例缩放、飞行器载荷运动等多种仿真演示要素。如果单独考虑每一种显示要素,不同的飞行仿真场景可在一定程度上增加仿真演示的灵活性,但这同时会带来另外的问题,如果需要模拟设计多种飞行仿真场,则相同的仿真演示要素在不同的场景中可能冲突。如果行星或飞行器比例缩放,那么在近距离观察飞行器运动时,飞行器可能发生碰撞;如果行星或飞行器比例不缩放,则在飞行器大范围机动时,飞行器可能小到看不见。如果飞行器运行轨道不改变,同样,相对于地球而言,飞行器极小;如果改变飞行器运行轨道高度,则飞行器上的某些载荷(如相机)的视场可能捕获不到目标。
3.3.2.2 设计约束
为简化行星际飞行仿真演示复杂度,在不影响仿真演示效果的前提下,列出算法设计约束如下:
1)空间仿真场景模拟以日心黄道坐标系为基准;
2)星空背景基于耶鲁星表中3000余颗星的位置和亮度绘制,每颗在远裁减面内的星都用相同大小的白色的点绘制,并根据其相对亮度调整透明度。
3)行星采用球体贴纹理实现,球体半径为真实行星半径大小,地球大气层高度为大气层实际高度。
4)太阳仅考虑位置的正确性,其大小保持不变,采用球体贴纹理实现。
3.3.2.3 比例归一化
大尺度行星际飞行仿真演示算法设计的核心思想就是对所有的演示要素按照真实比例1:1绘制,即对空间距离、仿真对象模型、轨道、载荷等显示要素不予缩放。
1:1绘制可以解决绝大部分仿真演示问题,例如成像对象不能进入相机视场、近距离观察飞行器,飞行器会发生碰撞、飞行器运动失真等等。总之,行星际飞行仿真按照仿真对象实际的距离和大小实现,这可以避免不同的试验程序自定义调整不同的显示要素。
设计约束的第3)项可以解决行星际的“合理性”显示问题。对于太阳的显示仅考虑其位置,太阳在三维太空中的位置将被准确的投影到屏幕上合适的位置。太阳的显示通过透明纹理贴图实现,大小保持不变,这与常识吻合。
3.3.2.4 最小视距与最大视距
最小视距的定义:最小视距首先是一个长度量,标示仿真对象在三维空间中的位置与视点之间的距离,其次,该距离是仿真对象从三维空间投影到二维屏幕上,且能够被观察者感知的最小距离。图3表示了视点与最小视距的关系。从定义可知,最小视距是一个被人为感知的长度量,不同的人可能具有不同的最小视距,即同样大小的物体在同样的位置,然后投影到屏幕上,不同的人可能感觉大小不一样。最小视距从定义上讲是一个三维空间中的长度量,但观察者在二维屏幕上能够感知的是一个二维区域的大小,即屏幕上有多少个像素表示该仿真对象。根据OpenGL透视原理,当物体投影到屏幕后,有的会认为1个像素时对应该物体的最小视距,有的会认为4个像素表现该物体时对应该物体的最小视距。

图3 视点与最小视距
最小视距虽然由观察者确定,但最小视距本身由OpenGL根据透视原理和渲染流程自动计算。
视点总是被绑定在空间坐标层次结构树的某个坐标系下。同样,各个仿真对象也在各自的坐标体系下运行,因此,总是可以精确的计算出各个仿真对象到视点的距离。
最大视距的定义:观察者认为仿真对象投影到二维屏幕上的物体不能再小(大小保持)时仿真对象距离视点的距离。最大视距同样是一个长度量,表示三维空间中的对象距离视点的距离。如果仿真对象大于最大视距,继续远离视点,此时需要放大对象显示比例(完全抵消OpenGL透视比例),使其随着距离的增大,在二维屏幕上的投影面积不变。图4表示最小视距与最大视距空间位置关系。

图4 最小视距与最大视距
3.3.2.5 放大最小视距外的仿真对象
1:1绘制不能解决的问题是在大尺度空间仿真场景中,飞行器做大范围机动时,用户需要了解飞行器当前的位置,但远处的飞行器已经超出了可见范围。
需要计算出仿真对象的最小视距,如果仿真对象在最小视距内(也就是说仿真对象可见),则由OpenGL根据透视原理自动计算仿真对象的大小。但如果观察者认为仿真对象已不可见(或者说,在屏幕上的投影不能再小),此时,如果仿真对象再远离视点,就需要放大仿真对象的显示比例,以满足仿真对象的可视需求。
例如:当飞行器机动到距离视点2km远处,此时用户认为飞行器需要人工干预放大飞行器比例,则2km就是该飞行器的最小视距。假如飞行器在2km处对应在屏幕上显示为25个像素(5×5),当飞行器继续远离直至距离视点10km,在OpenGL透视机制的作用下,此时飞行器在屏幕上显示为4个像素(2×2),如果用户认为4个像素是满足仿真对象可视需求的最小投影,则10km就是该飞行器的最大视距。如果视点与飞行器距离大于最小视距,需要对飞行器的显示比例进行适当放大,但不能大于25个像素(以避免造成距离视点越远,物体反而变大的情况)。如果视点与飞行器距离大于最大视距,则需对飞行器显示比例充分放大,使其在屏幕上的投影面积始终保持在4个像素大小。
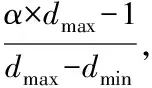
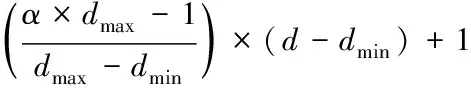
(1)
当视距大于最大视距时,该段直线为α×d,分段函数可描述为如下公式
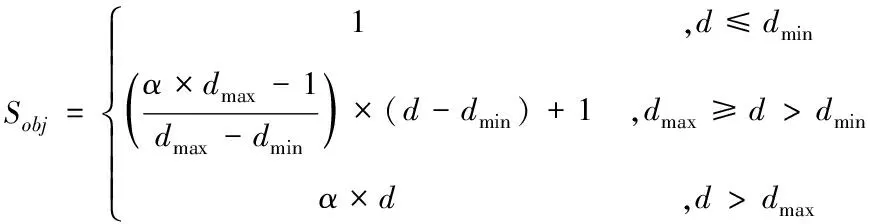
(2)

图5 对象缩放比例与视距直线连接关系
如图6所示,如果不考虑分段,从单一公式描述,则可知连续平滑曲线在f′(dmin)=0,f′(dmax)=α,飞行器缩放比例实为问题:
H(x0)=f(x0),H′(x0)=f′(x0)
H(x1)=f(x1),H′(x1)=f′(x1)
的解。根据三次Hermite插值定理,飞行器缩放比例可如下式表示

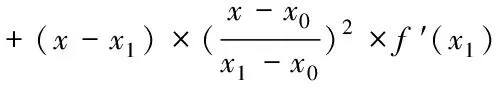
(3)
其中x0=dmin,x1=dmax,f(x0)=1,f′(x0)=0,f(x1)=α×dmax,f′(x1)=a。
综上:
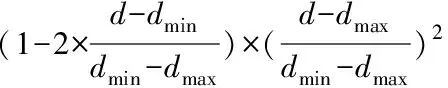
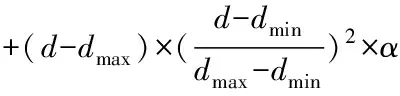
(4)
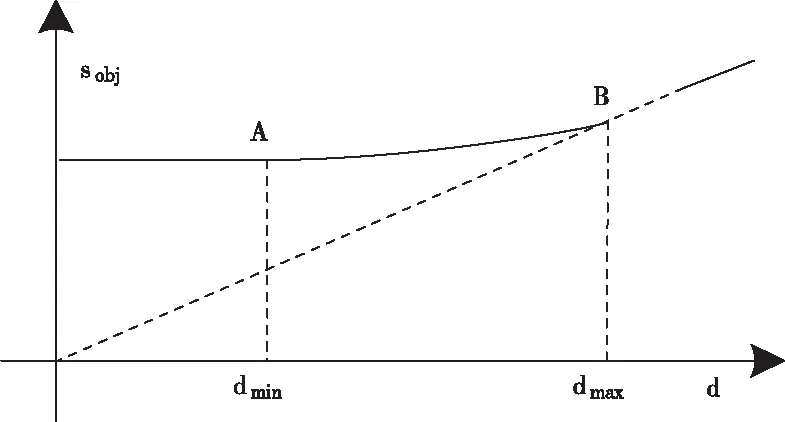
图6 仿真对象缩放比例与视距平滑连接关系
在实际使用过程中,需要首先确定dmin、dmax和α值,再根据视距实时按照式(4)确定各仿真对象的缩放比例。
4 仿真验证
根据上述算法,基于开源图形引擎OpenSceneGraph[7-8]及osgEarth[9-10]开发了地月运动仿真系统,图7左边表示太阳系各行星运行轨迹,右边是地球在赤道坐标系与黄道坐标系网格下的运动仿真,用户能够在行星及其卫星之间切换视点并拉近观察太阳、月球及各行星状态。图8左边表示飞行器地月运动轨迹,右边则是将视点绑定到飞行器上,通过交互控制贴近观察飞行器某载荷的开盖过程(蓝色椭圆圈内)。
5 结语
本文分析了行星际飞行仿真特征,基于视觉透视原理和视点控制机制设计了一种行星际飞行仿真视点运动控制算法。当仿真对象与视点的距离小于最小视距时,由OpenGL透视机制自动控制投射到显示屏幕上的各空间仿真对象的大小;当视距大于最小视距但小于最大视距时,部分抵消OpenGL透视机制所带来的比例缩小值,当视距大于最大视距时,则全部抵消OpenGL透视机制带来的比例缩小值。另外,在大尺度空间场景仿真过程中,当需要了解细节时(如观察载荷运动),可采用多观察者方式[11]等形式辅助助实现。

图7 日心黄道坐标系下的行星运动仿真
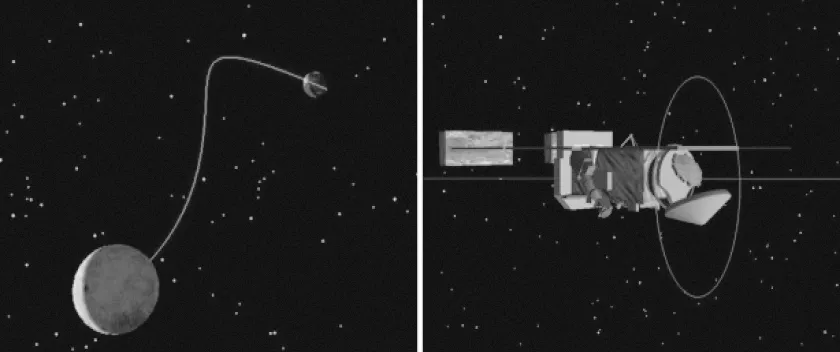
图8 飞行器地月运动仿真

