蝴蝶结膜面的力学性能试验与仿真分析

杨 晓，王雪明，何 巍，顾文华

(中国特种飞行器研究所，湖北 荆门 448035)

1 引言

系留气球利用囊体内轻于空气的气体提供的静升力长时间驻空，主要用于低空侦查、通信中继以及环境监测等领域。近年来，随着薄膜结构和新型复合材料等技术的快速发展，针对系留气球的研究也受到越来越多人的关注。蝴蝶结也被称为抓手或载荷帘，通常热合在系留气球的囊体表面，起着连接外部索具和传递索具荷载的作用，主要由衬布、承力条和拉环组成。衬布采用可以与囊体材料相融合的新型复合材料，承力条具有多种形式(织物类、织带类)，热合或者胶结在衬布表面，拉环用于连结承力条和外部索具。实际工程中根据承载力的不同，可对承力条的数量、材质及扇形面积进行相应调整。

由于蝴蝶结具有良好的荷载扩展性，且制造工艺简便，所以广泛应用于系留气球，飞艇等大型柔性结构中，其优良的力学性能对整体结构的安全性具有非常重要的影响。蝴蝶结通常采用编织的新型复合材料薄膜，而纤维织物具有复杂的微观结构且编织结构具有方向性，故在材料层次和结构层次表现出明显的非线性和各向异性。在实际中，蝴蝶结基本处于双向张拉状态，所以研究在相同荷载条件下的膜材力学响应特性非常关键。有关双轴拉伸力学特性的研究表明，膜材的双向受力性能具有明显的非线性，且弹性参数受到不同应力比和应力组合的影响。鲁国富等对蒙皮材料进行7种应力比下的双轴拉伸试验，建立应力弹性常数响应面，并通过有限元仿真验证其非线性模型的正确性。陈建稳等针对某芳纶纤维层合膜材进行了一系列双轴拉伸试验，得到了应力空间中材料弹性参数的响应曲面，并总结应力比和应力组合对膜材双向拉伸力学性能的作用规律。目前国内外对蒙皮材料的力学性能研究较多，但对蝴蝶结的研究相对较少，所以有必要深入研究它的力学响应特征。

首先设计了蝴蝶结试件的力学响应试验。研究试件在双向1.6kN张拉荷载下，在蝴蝶结拉环处分级施加面内拉力2kN、4kN、6kN、8kN、10kN时膜面产生的变形、应力与应变响应；然后利用有限元软件对试验过程进行数值仿真分析；最后提出一种将试验与仿真结果定量对比的方法，对试验与仿真结果进行定量对比和误差分析。验证了仿真方案的可行性以及实验数据的准确性。

2 蝴蝶结试验

2.1 试件材料及结构

蝴蝶结试件的蒙皮材料与承力条分别采用具有高强度，高比强，高模量的芳纶纤维层合膜材。

将蝴蝶结布置在蒙皮试件中部位置，如图1所示。蝴蝶结承力条的弯折后成一定夹角，如图2所示，每根承力条由多层膜材焊接而成。

图1 蒙皮试件示意 图2 蝴蝶结示意

2.2 试件预处理

首先将预制好的散斑贴在如图3所示的矩形红框内，作为试验测试初始区域(最终区域取决于试验设备)。由于柔性膜材具有很强的非线性且加载过程容易产生褶皱，为了方便与数值结果对比且提高对比结果的准确性，提出一种定量对比的方法。在试件表面的重点关注区域，以50mm为间距，水平做编号为～的矩形区域，测量区域内所有结点的水平应变(垂直加载方向)、剪切应变。竖直做编号为～的矩形区域，测量区域内所有结点的竖直应变。沿承力带方向做编号为～的矩形区域，测量区域内所有结点的最大主应变。在每个工况下，取每个矩形区域中所有测试点的平均值作为最终结果。对比传统的单节点数值对比方法，该方法显著的提高了结果的准确性和可靠性。其中，矩形区域的边长均为15mm，且应保证各区域测试数据点不少于10个。散斑区域分布位置如图3中小方块所示。

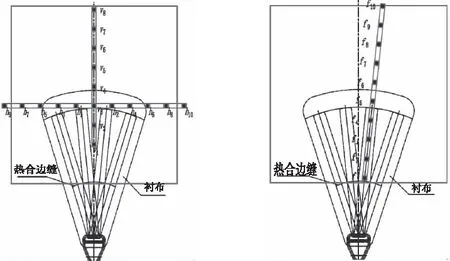
图3 矩形区域分布位置

2.3 试验设备

试验环境温度应在-5℃-40℃之间，相对湿度应小于85%RH，采用典型连接结构强度试验平台，平台采用自平衡框架的设计方式，无需额外约束，应用PLC程序控制，能够实现试验件的自动张紧、加载、采集等功能。采用三维数字散斑应变测量及分析系统(DIC-3D)获取试件加载后的位移、应力和应变数据。

2.4 试验方法

首先将预处理后的试验件安装在平台上，完全约束试件的四条边，且施加双向1.6kN的张紧力，作为试件的初始状态；然后架设照明系统，使光圈照射在散斑区域，以提高图像的分辨率；接着架设图像采集系统，对其进行标定并锁定焦距，链接遥控拍照控制器，设定相机在每循环中以固定间隔时间拍摄相同数量的照片，调试照相机，使其能清晰拍摄到测试区域的散斑情况；然后启动试验机，以60mm/min速度对蝴蝶结拉环施加面内载荷至2kN，待稳定后观察散斑变形情况并拍照记录后继续分级加载至4kN，6kN，8kN，10kN，重复上一步。最后利用DIC-3D对每级的照片进行计算处理，得到散斑区域内各工况下的应力、应变和位移场结果。采集标定区域内所有测量点的数据后进行记录。

2.5 试验结果

由于试验设备的局限性，只能获取部分散斑测试区域的结果，最终选取10kN的工况结果进行分析。

2.5.1 h区域结果分析

图4为试件的部分散斑区域相对于初始状态的水平应变云图。可以看出最大水平应变处于承力带两侧。由于承力条由5层膜材粘合而成，刚度明显增加，牵引两侧膜材发生变形。最小水平应变出现在中间位置的承力条区域，随着荷载的增加，应变值由2kN荷载下的-0.4%逐渐增大10kN荷载下的-7.6%，与此同时，膜面局部发生受压变形与褶皱，但褶皱占主要成分。

图4 水平方向应变云图

由于试验设备原因，只能获取～区域结果，各个工况下的数值结果如图5所示。对比水平应变图，随着荷载的增加，各数据点的应变值呈现增加的趋势。并且中间点的水平应变绝对值大于其它数据点，可见蝴蝶结荷载变形过程中，因承力条的刚度大，区域因局部刚度小，呈现水平负应变，表现出水平收缩。

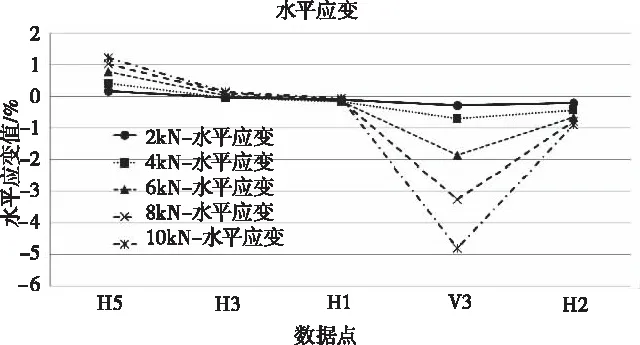
图5 h数据点水平应变结果

图6为试件的剪切云图，可见区域的剪切应变绝对值最小，向两侧扩展过程逐渐增大，在拉伸过程中，两侧表现出较大的剪切变形，区域以拉应变为主。图7为各个工况下的数值结果，随着荷载的增加，各区域沿两侧扩展时的应变绝对值逐渐增大，与云图结果一致。

图6 剪切方向应变云图

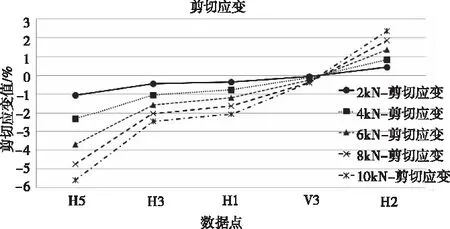
图7 h数据点剪切应变图

252区域结果分析

图8为试件的部分散斑区域相对于初始状态的竖直应变云图，可以看出承力带区域的竖直应变相对较小。最大竖直应变出现在承力带下侧均匀区域，随着荷载的增加，应变值由2荷载下的092增大至10荷载下的265。

图8 竖直方向应变云图

试验获取的～区域各工况下的数值结果如图9所示。对比竖直应变云图，随着荷载的增加，各数据点的应变值呈现增大的趋势。并且中间点、的竖直应变出现较大跃升，主要是承力条刚度较大，点以内属于承力条区域，因刚度大导致应变较小。点在承力条区域之外，因单层膜材刚度较小，导致应变值出现较大提高。

图9 v区域竖直应变图

253区域结果分析

图10为试件的部分散斑区域相对于初始状态的最大主应变云图，试验获取的～区域的数值结果如图11所示。随着荷载的增加，各数据点的应变值呈现增大的趋势。其中，、区域的竖直应变出现较大跃升，是因为承力条刚度较大，点以内属于承力条区域，因刚度大而应变较小。点在承力条区域之外，因单层膜材刚度较小，其应变值出现较大提高。

图10 最大主应力应变云图

图11 f数据点最大主应变图

3 数值模拟

3.1 有限元建模

利用三维建模软件Catia对蝴蝶结试件建模后导入中预处理，根据图3试验件中标定的矩形区域位置和散斑位置，在模型中设置相应的节点集合，以方便在后处理中提取对应的数值结果。由于膜材为柔性结构，实际中不可抗压及抗弯，所以为模型划分精细化网格时，采用能考虑几何大变形且不抗弯的膜单元M3D3和M3D4。为模拟试件不同区域的铺层效应，分区域设置材料厚度如图12所示。

在膜材试验过程中出现了较大的几何变形，且为缓慢拟静力加载，为准确模拟实验过程，数值仿真模型采用考虑几何非线性的通用静力分析。为了提高模型的收敛性，分为两个分析步，第一分析步通过设置位移边界条件来施加与试验相同的膜面预张力，以此作为模型的初始状态。第二分析步在蝴蝶结拉环处逐渐施加拉力，均打开几何非线性开关。

图12 10kN工况下的应变云图

依据试验对模型施加边界条件，左侧边界为固定约束，其余三边均施加适当的法向位移以模拟试验中1.6kN的预张力。实验平台每边对膜材约束较弱，模拟自由双向应力状态，计算模型同时释放横向约束，如图13所示。

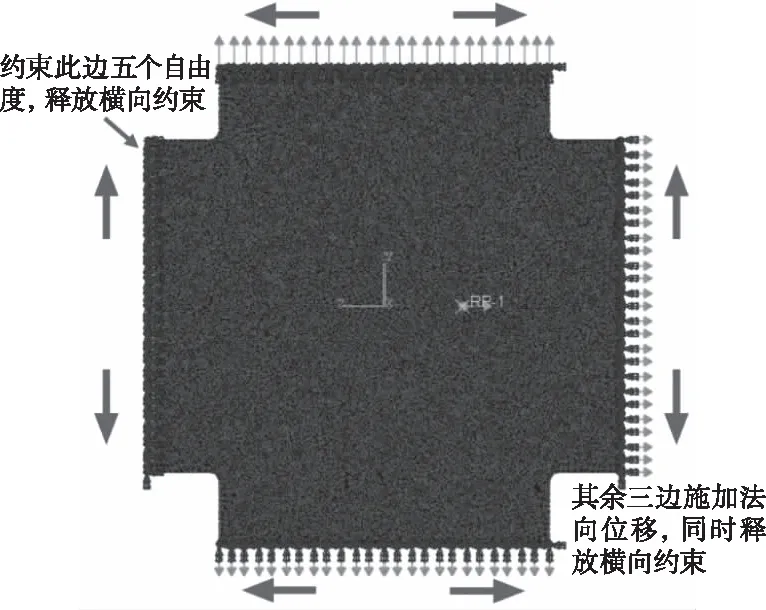
图13 数值模型边界约束

为模拟集中加载条件，将5层厚度区域的边结点与加载参考点(蝴蝶结拉环)耦合，采用分布耦合方式连结，如图14所示。分布耦合可将荷载传递到膜材的耦合点上，而不会约束膜材耦合点间的相对自由度，膜材耦合点依然保留独立变形的能量，以准确实现加载过程。

图14 分布耦合方式加载

3.2 数值模拟结果

选取10kN工况下的结果进行分析。图15-图22分别为模型相对于初始状态下的水平，竖直，剪切方向的应变，应力与位移云图。

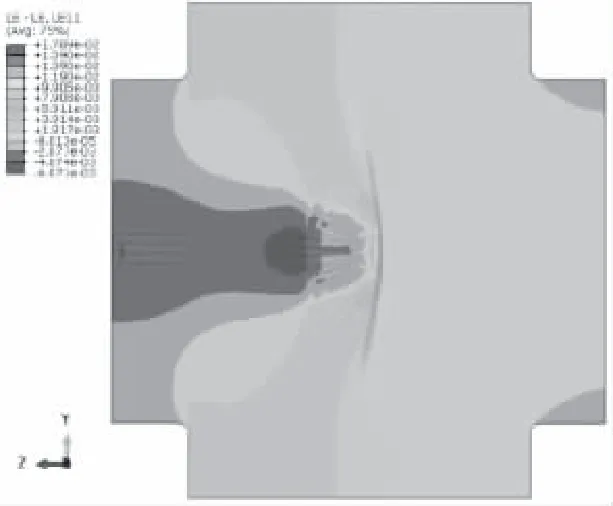
图15 水平方向应变云图

图16 水平方向应力云图

图15-17为水平方向的数值结果。可看出应力云图与应变云图表现一致，应变、应力集中出现在承力条的顶端部位，在承力条两侧出现较大的应力分布，并持续延续到夹持边界。可见在加载过程中，试件上下两侧边界处对变形提供一定的约束。在承力条受拉荷载的相反方向，出现水平受压的应变、应力区间。蝴蝶结试件在水平方向表现出对称的位移云图。

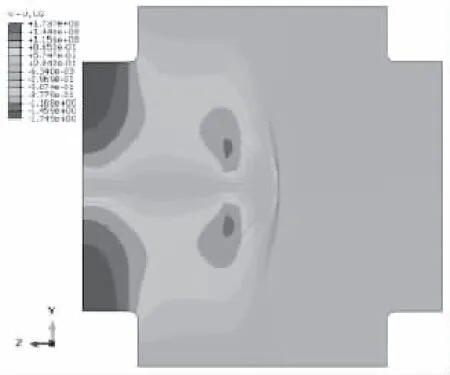
图17 水平方向位移云图

图18-20为竖直方向的数值结果。可看出应力云图与应变云图表现一致。承力条受荷载方向的另一侧出现较大的应力分布，并持续延续到夹持边界。在承力条外侧，单层膜材区域出现较大应力，该区域是结点受力较重要的位置。蝴蝶结试件在竖直方向表现出对称的位移云图。在试件加载位置处具有最大的变形，变形自承力条区域向边界逐渐递减。

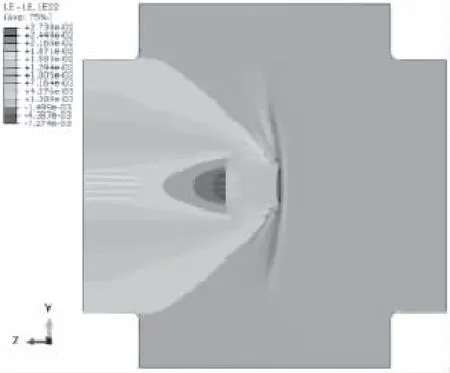
图18 竖直方向应变云图

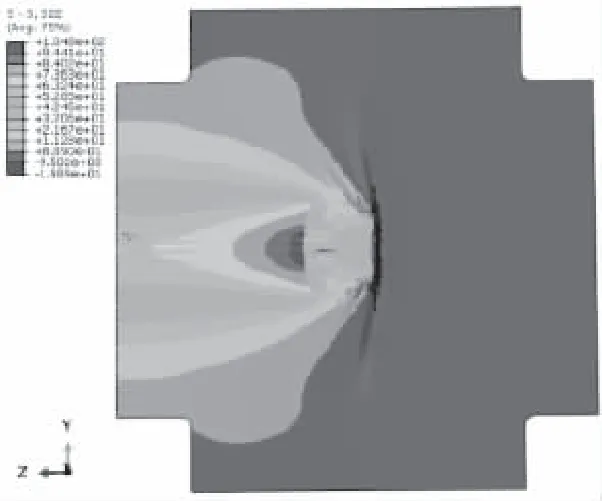
图19 竖直方向应力云图

图20 竖直方向位移云图

图21-22为试件相对于初始状态的剪切应变云图。可以看出应变呈近似对称分布，下端的应变最小，上端最大。受力过程中变形主要发生在承力带两侧的单层材料部分，随着荷载的增加，承力带两侧的褶皱区域越来越明显。

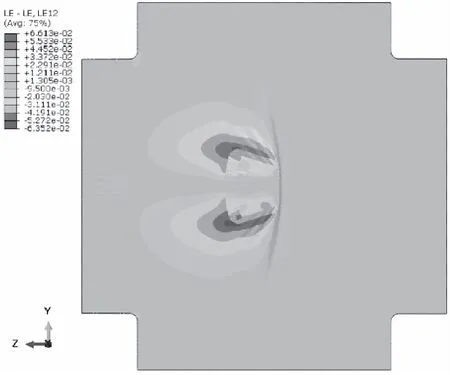
图21 剪切方向应变云图

图22 剪切方向位移云图

4 试验与仿真结果对比分析

根据图3标定的矩形区域位置，分别提取10kN工况下试验与仿真的数值结果，做定量对比和误差分析。

4.1 h区域结果对比

因水平应变绝对值接近零，对比计算值与试验值的意义不大，仅对比了剪切应变的误差情况，如表1所示。可以看出试验数据与仿真结果对比良好。虽然膜单元依然具有抗压的能力，但在集中荷载拉伸下，中间受压单元的剪切应变接近于零。微小的测量、计算偏差就能引入巨大的相对计算误差，因此没有计算相对误差。最终平均误差为5954。

表1 h区域剪切应变数据对比表(%)

4.2 v区域结果对比

表2中列出了区域的竖直应变误差情况，因点在测量区域边缘，由于测试误差较大将其除去。组区域与试验结果吻合较好，在承力条区域，因刚度较大纵向应变较小。自点开始进入单层膜材区域，因单层膜材刚度较小，其应变值出现较大提高。最终平均误差为8019。

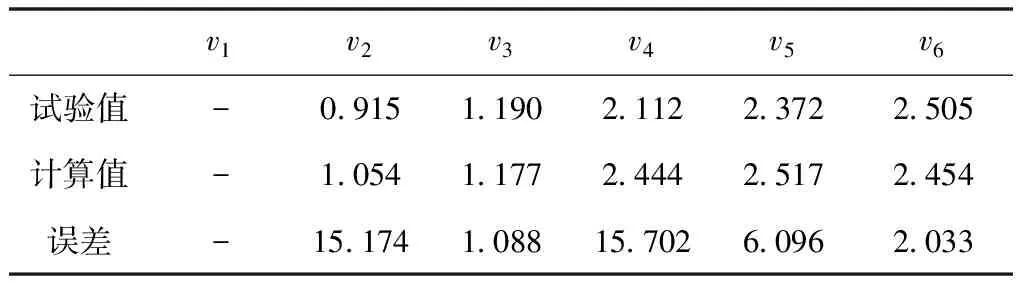
表2 V区域竖直应变数据对比表(%)

4.3 f区域结果对比

表3中列出了区域的最大主应变误差情况，因f点在测量区域边缘，测试误差较大，所以除去。f组数据与试验结果趋势基本吻合，在承力条区域，因刚度较大，应变值较小。f是承力区域到单层膜面区域的过渡位置，单层膜材刚度较小，其应变值出现较大提高，存在一定的褶皱变形。计算误差与试验误差较大，最终平均误差计算值6.757%。

表3 f区域最大主应变数据误差计算表(%)

5 结论

通过数值仿真与试验对蝴蝶结处于不同荷载下的力学响应进行分析。研究了蝴蝶结膜面在试验工况下的变形、应力与应变响应及分布规律。提出一种试验与数值模拟结果定量对比的方法，发现对比结果的误差在10以内，验证了试验数据的有效性与数值模拟方法的正确性。针对其它的同类试验可以利用该仿真方法进行分析，对蝴蝶结的力学设计与试验研究有着指导借鉴的作用。