人伞系统的六自由度运动仿真

周晓光，朱 鹏，张源原，路 欢

(海军航空大学，葫芦岛 辽宁125001)

1 引言

跳伞是飞行员在作战和训练突遇险情必须具备的救生技能，也是伞兵的基本训练科目。目前常规的军事跳伞科目训练，通过在伞降场实地开展，具有高危险、高耗时、高成本的特点，而利用虚拟现实技术实施军事技能型训练，在减小训练危险、增强训练环境适应性和降低训练成本等各种方面有着传统训练方式不可比拟的优势，是未来军事训练发展的重要方向之一。

跳伞模拟器是采用虚拟现实技术的训练模拟机之一，可以根据仿真数据生成实时图像，通过头戴式显示器的虚拟场景构建模拟人伞系统伞降过程。利用跳伞模拟器，训练者可以更有效、更安全地训练，也可以降低训练成本，增加训练针对性。跳伞模拟器通常由控制框架、可视化系统、人伞系统运动模型和管理平台组成，由于各模块的模拟数据主要来源于人伞运动模型，因此进行精确的人伞系统运动仿真是保证跳伞模拟器真实性的关键部分。

在文献[4]中，Dellicker等人介绍了虚拟现实技术在伞兵训练中的应用，给出了模拟器的组成和总体结构。但其只关注视觉生成方法，没有考虑人伞动力学。一般来说，降落伞运动过程包括以下阶段：离机后自由坠落，伞包打开至拉直，伞衣充气和伞衣充满到稳定下降的稳降过程。目前在我军的常规伞降训练中，大多采用绳拉一级或二级开伞，在上述伞降运动过程中，从跳伞员离开飞机到伞开正常只有短暂的几秒钟，这几秒里跳伞员近似处于抛体自由下落状态，姿态的可控性不大；而自跳伞员感受到开伞冲击力(伞开正常)开始一直到安全着陆，则有几分钟之久，这段时间是除伞降特情处置之外降落轨迹操纵的重点，如果对这段时间尽可能全面的模拟，则能大幅度地提高模拟训练的效果。

目前，关于降落伞稳降阶段的运动模型建立已有较多研究成果，如文献[7]以可控圆形降落伞为研究对象，建立了物伞系统的六自由度运动模型，但其通过被称为气动人工肌肉的伞绳操纵，与人伞操纵过程不同。郭叔伟等研究了飞行力学仿真环境下降落伞系统动力学建模问题，对降落伞稳降阶段进行了分析，但未考虑任何控制输入。文献[9]建立了火星降落伞与运载器系统的六自由度非线性数学模型。但降落伞模型是由飞行器控制的，也区别于人用降落伞。而利用跳伞模拟器进行跳伞训练，很重要的一点就是要模拟跳伞过程中的各类运动。目前关于人伞系统运动仿真的研究还较少，大多基于三自由度平面模型进行仿真模拟，如张宝等从跳伞模拟器研发出发，给出了人伞系统稳降阶段的操纵方法，并建立了跳伞模拟训练评估标准，但其模拟过程在二维平面内进行，与实际跳伞过程有一定差距。除此之外，国内外大量的伞降试验表明，伞降区域风场对伞降过程将产生较大影响，在跳伞模拟器训练过程中，若能有效模拟不同风场环境下的人伞系统运动过程，并练习采取不同操纵方法以实现风场扰动下的稳定伞降，对提高伞降训练水平具有重大意义。

综上所述，本文针对跳伞模拟训练系统研发需要，在吸收前人研究成果的基础上，以人伞系统为研究对象，建立了高精度的六自由度人伞运动模型，并根据训练实际，引入跳伞员操纵力与力矩模型，实现人伞系统运动操纵仿真。在此基础上，选取了不同风场环境作为计算条件，对人伞运动过程进行数值仿真，分析了相应风场环境下人伞系统应采取的操纵方法，可使跳伞员预先熟知降落轨迹，控制好降落过程中的空中位置，以实现躲避地面障碍物，安全准确地在目的地着陆。

2 人伞系统建模

2.1 人伞系统描述

本文研究跳伞员稳降阶段的运动过程，此时降落伞已完全打开，考虑到实际伞降着陆过程中，跳伞员身体被操纵带束缚，且姿态需按照“三紧一平”要求，严禁接地时开腿开脚，可对人伞系统做出如下假设：

1)降落伞伞衣与跳伞员形成一个刚性系统。

2)跳伞员的空气动力和力矩可以忽略不计。

3)降落伞气动力作用于伞衣的压心，且与伞衣的质心不重合。

4)人伞系统关于伞衣质心与人体质心连接线轴对称。

基于文献[7]研究成果，分别定义地理坐标系，人伞系统体坐标系，为地理系原点，为伞衣开口平面的伞衣基准平面中心圆点，如图1所示，和轴在伞衣基准平面内，轴指向跳伞员。

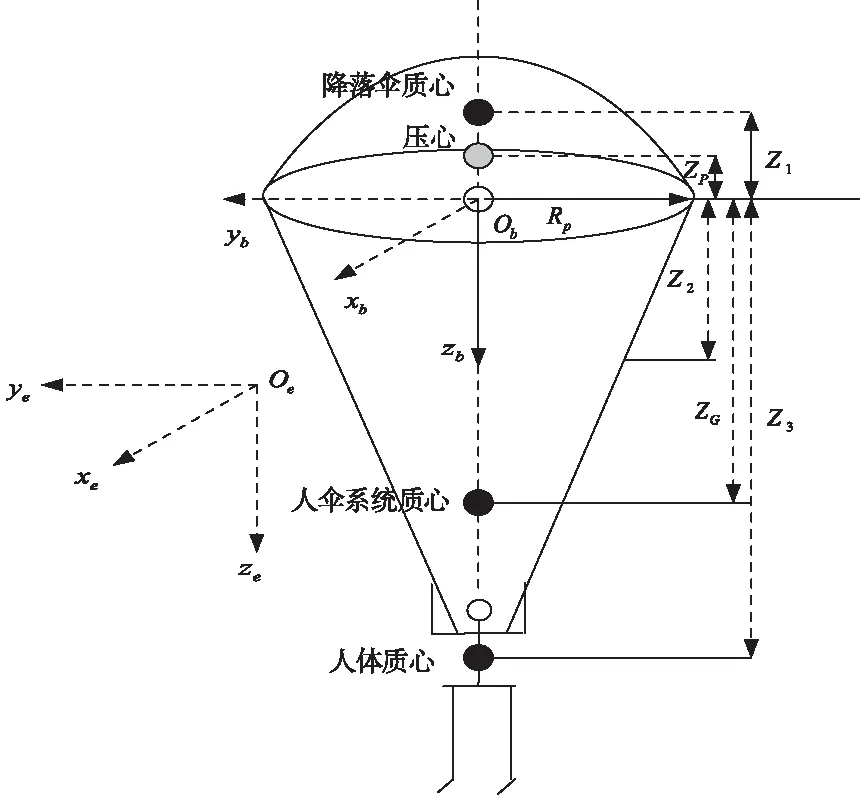
图1 人伞系统基本结构

人系统是由一个普通的半圆形伞体、可操纵伞绳与背负操纵带的跳伞员组成，跳伞员与伞绳之间通过降落伞操纵带连接。人伞系统外形尺寸如图1，其中为伞衣基准面半径，、、、、分别为体坐标原点到伞衣质心、伞绳质心、人体质心、伞衣压心、人伞系统质心的距离。记伞衣重量、伞绳质量、跳伞员的质量分别为、、。

2.2 人伞系统六自由度运动方程

现有的人伞系统动力学模型通常使用牛顿-欧拉法建立，建模过程需要根据刚体几何关系消去多余的自由度，人伞系统为复杂的多体系统，计算求解较繁琐，而拉格朗日方程法利用微分方程求解，免去了不需要的约束力计算，更适用于人伞系统。利用拉格朗日方法，可得到降落伞系统的基本运动方程，其一般形式如下

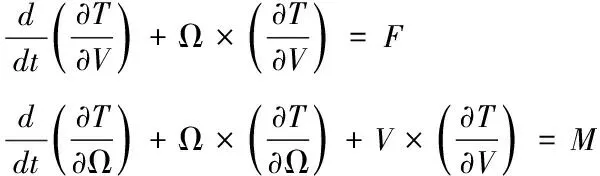
(1)

上式又称为克希霍夫(Kirchhoff)方程，式中为系统的动能，=[]和=[]分别为作用在降落伞系统上的外力和外力矩，人伞系统在体坐标系共有6个自由度，和Ω分别为系统的速度和角速度矢量，其在体坐标系三轴分量分别为，，、，，，上式在体坐标系中展开的分量形式如下

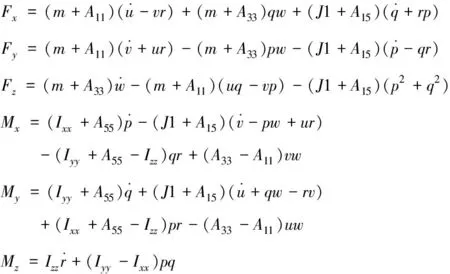
(2)

其中

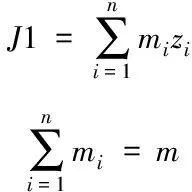
(3)

另外，，，表示人伞系统在体坐标系各轴上的转动惯量，其计算方法可参见文献[7]，不同点在于人体惯性参数可采用Hanavan人体模型计算。、、、表示降落伞运动过程的附加质量，其可用于说明降落伞改变周围流体动能所需的力与力矩，文献[11]给出了圆形伞附加质量的近似表达式

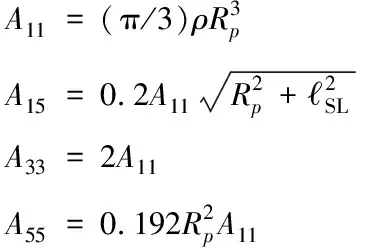
(4)

以下运动学方程式可用于确定降落伞的姿态，、、分别表示人伞系统的滚转角、俯仰角、偏航角

(5)

最后，人伞系统在地理坐标系中的位置(，，)可通过下式求解，而人伞系统高度=-

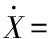
+(cossincos+sinsin)

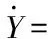
+(sinsincos-cossin)

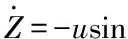
(6)

至此，可以通过式(2-6)确定人伞系统的速度、角速度、姿态角和位置共12个状态值，有关状态值的定义可参见文献[7]。

2.3 风场模型

风是大气运动而产生的，风速的大小和方向可以反映出大气的运动状况，风随空间和时间的变化分布称为风场。降落伞系统在大气环境中易受风场的影响，不同形式的风场对降落伞系统的轨迹、运动速度、姿态等都有不同程度的影响。这里所研究的主要是变化风，采用风场模型来模拟实际的风场，常见的风场模型有平均风场模型、紊流风场模型和突风风场模型等。在研究中一般仅考虑风场在水平分量上的作用，不考虑垂直分量上的影响。本文风场模型采用平均风叠加紊流风的方式建立，具体表达式如下

()=()+()

(7)

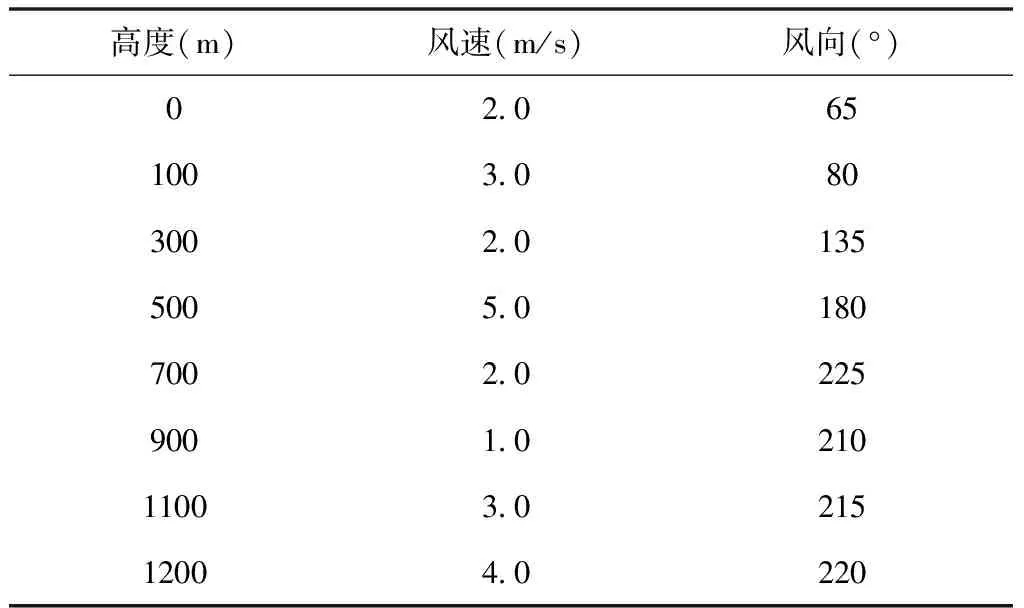
表1 风场数据表

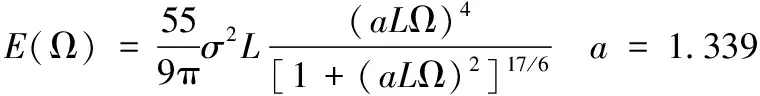
(8)

式中，为紊流强度；为紊流尺度；Ω为空间频率，它适用于15～20以下的大气层。

由于扰动风矢量一般是基于地理坐标系给出的，因此，对于式(7)，需要将地理坐标系下的风速矢量通过坐标变换转化到机体坐标系中

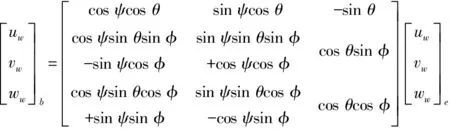
(9)

2.4 力与力矩模型

在给出具体的力和力矩的表达式之前，由于存在风场扰动，还需将速度矢量作如下变换

(10)

其中，、、为人伞系统体坐标系原点的空速三轴分量，其与降落伞压心处空速、、有如下关系

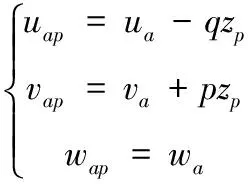
(11)

对于轴对称人伞系统，因其气动特性同样具有对称性，因此气动计算时通常直接使用其中心对称轴与空速矢量的夹角——即总攻角，来代替迎角和侧滑角，可以直接根据体轴系下的空速分量由下式进行计算

(12)

稳降阶段人伞系统所受外力和外力矩的矢量形式为

(13)

式中，是人伞系统所受的重力；是降落伞所受的气动力；是跳伞员操纵产生的控制力；是降落伞的气动阻尼力矩；是跳伞员操纵产生的控制力矩；和分别是在人伞系统体坐标系下，人伞系统质心和降落伞压心的位置矢量。式(13)中重力、气动力与气动阻尼力矩的分量形式如下：

(14)

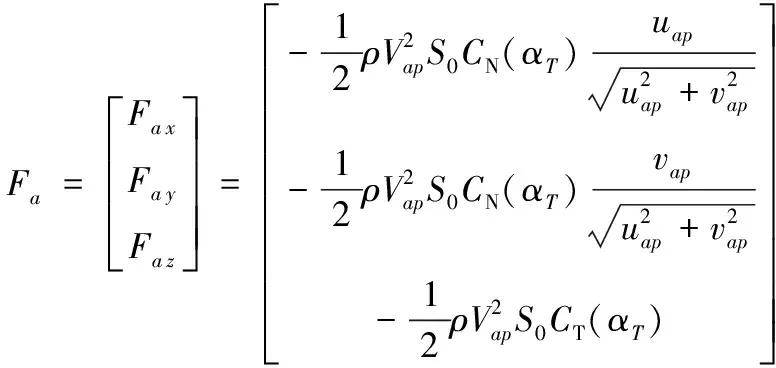
(15)

(16)

式中，为空气密度；()、()为气动力法向力系数和轴向力系数；为降落伞参考半径，为降落伞参考半径；、、为人伞系统的气动阻尼力矩系数，取值采用给出的圆形伞气动数据。

不同于物伞系统，式(13)中存在操纵力与操纵力矩。对于一般的训练圆形伞来说，其每根伞绳都编有序号，而第一和最后一根伞绳上端为伞衣排气口，下端会缝上短绳，短绳上再拴操纵棒。当需要左转时，拉下左操纵棒，即可带动伞绳向下运动，使排气口左侧的伞衣向里凹，而排气口右侧的伞衣就相对凸起，伞衣内的空气经排气口向左后方排出，同时产生一个相反的作用力，将伞衣向右前方推，则降落伞向左转动。同理，拉下右操纵棒时，降落伞向右转，本文将拉左右操纵棒的操作方式分别记为与。

另外，圆形训练伞还存在两根操纵带，每根操纵都有前拉和后拉两种操作方式，本文将其分别记为左前、右前、左后、右后。当跳伞员拉扯操纵带时，相应操纵点处的伞衣被改变形状，以下拉左前方操纵带()为例，拉力使伞衣变形后，左前侧伞衣边缘流过气流的曲折增大，导致了该方向涡流增强，左前部分内外压力差变大，整个伞体产生左前方的力，其可分解为前侧力和左侧力，受力分析如图2所示。由于伞体的稳定性设计，带来的影响并不明显。而的受力点并不经过受力压心，由图2可见该处的受力导致了一个正的轴方向力矩，使降落伞发生顺时针旋转。同理，右后()操纵也会导致正的轴方向力矩，上述分析结果也与人用伞操纵手册描述相符。相对的，右前()、左后()操纵即可产生逆时针旋转效果。同理还有多操纵带的操纵方式，如侧拉单侧双操纵带会产生一个指向该方向的侧力，且能消除轴偏航力矩。其次是加减速方面，当同时拉四个操纵带，该操纵会使伞衣的整体投影面积减小。垂直方向上受阻力减小，垂直方向上有一个加速的过程。

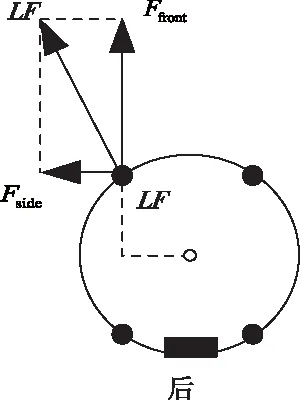
图2 操纵受力分析

由于降落伞操纵效果的产生并不是一个瞬间完成的过程，为了准确描述操纵过程，本文假设操纵量出现后，操纵效果存在一个持续时间，但操纵效果会随时间的增加而减弱。若在上一次操纵效果内出现再次操纵，将对操纵时间初值进行重置。通过上述描述即可将操纵量转换为操纵效果，操纵产生的人伞系统体坐标三个方向的受力Δ、Δ、Δ大小如下，并使用参数、、作为操纵的可调参数，、、是三个方向的并行操作增益

-(++··)]

-(++··)]

+(++··)]

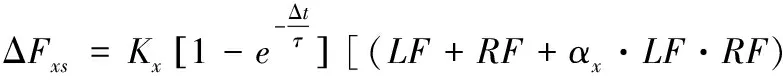
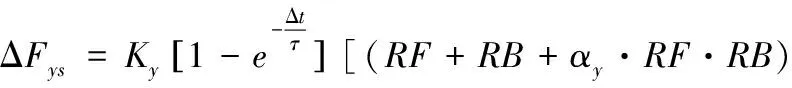
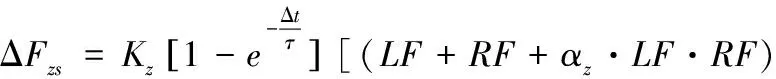
(17)

操纵力矩方面，通过操纵描述和分析可知，人伞系统操纵将产生如下偏航力矩

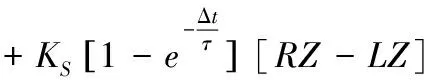
(18)

式中，、、、、、∈{0，1}，当跳伞员进行降落伞操纵时，相应操纵方式输入值为1，其余为0。Δ为操纵效果延时时间，、为力矩操纵可调参数，至此，人伞系统操纵模型建立完成。

3 仿真分析

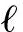
为了更全面地模拟人伞系统运动过程，将系统的仿真工况分为3组：第1组对人伞系统无扰动情况进行模拟，第2组在此基础上分别加入平均风模型与紊流模型，分析人伞系统在大气扰动下的运动情况。第3组以平均风扰动下的人伞系统运动过程为例，通过施加适当的操纵，以分析跳伞员风场扰动下的伞降过程。

表2 操纵系数

3.1 无扰动情况的仿真结果

首先给出人伞系统无扰动无操纵情况下的仿真结果，仿真结果如图3～4所示。可以看到，在无扰动的理想情况下，系统垂直方向上的下落速度在开始仿真后迅速减小，并最终维持在了=48，伞降速度符合小于=55的安全范围，而系统在Oxy平面方向的运动主要由人伞出舱的水平速度决定，在空气阻力的作用下，平移速度也收敛于=161，人伞系统降落轨迹表现为一条稳定倾线。本文将其降落点为圆心，半径50的范围设为仿真伞降的预定降落区域，用于后文扰动情况下的落点分析。

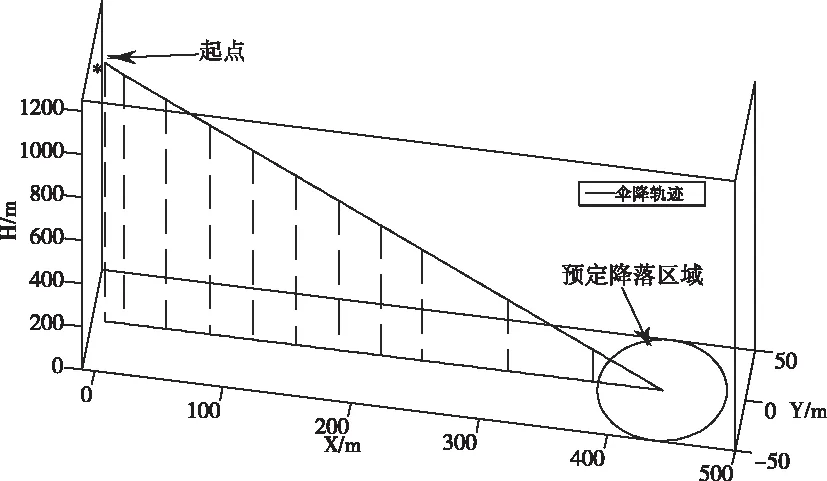
图3 伞降三维轨迹图

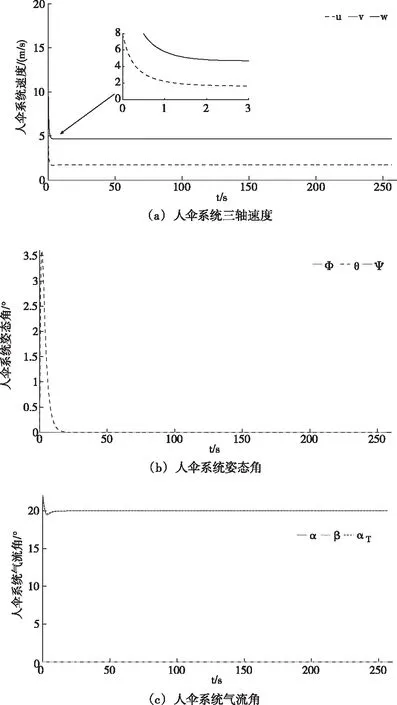
图4 无扰动无操纵情况的仿真曲线

进一步观察图4中的仿真曲线可以发现，在人伞系统稳定下降的初始阶段，由于降落伞气动力的作用，人伞系统出现俯仰角=35°的前倾，随后在系统重力矩的平衡下迅速恢复平衡状态，即无姿态角的垂直降落，而系统总攻角与迎角快速收敛于20°，表明本文采用的圆形降落伞为存在平衡攻角的不稳定型伞，这与文献[13]给出的不稳定型伞的气动规律表现出一致性。

3.2 风场扰动的仿真结果

本节分析风场扰动对人伞系统运动过程的影响，根据风场模型不同，仿真结果分为两部分，图5～6、为平均风扰动下系统运动状态。由图5可以看到，人伞系统在风场扰动下运动轨迹发生偏移，最终降落点超出了预定降落区域。而分析其速度变化量可以看到，在不考虑垂直风场的情况下，系统稳定下降速度几乎没有波动，表明水平方向的风场扰动不会影响伞降垂直方向的受力平衡。进一步观察图6，可以发现人伞系统三轴速度的变化与风速密切相关，且在气动力达到平衡状态过程中，人伞系统的绝对速度越来越接近风速，即对空相对速度为越来越小，使系统运动轨迹的变化基本决定于风速的改变。这表明若能提前获得伞降区域的风场信息，可通过本模型有效模拟伞降轨迹，提前预测降落区域，甚至通过改变伞降起点以使跳伞员顺利降落至预定区域。

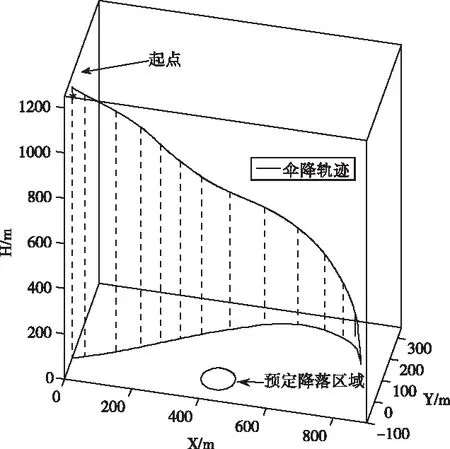
图5 伞降三维轨迹图

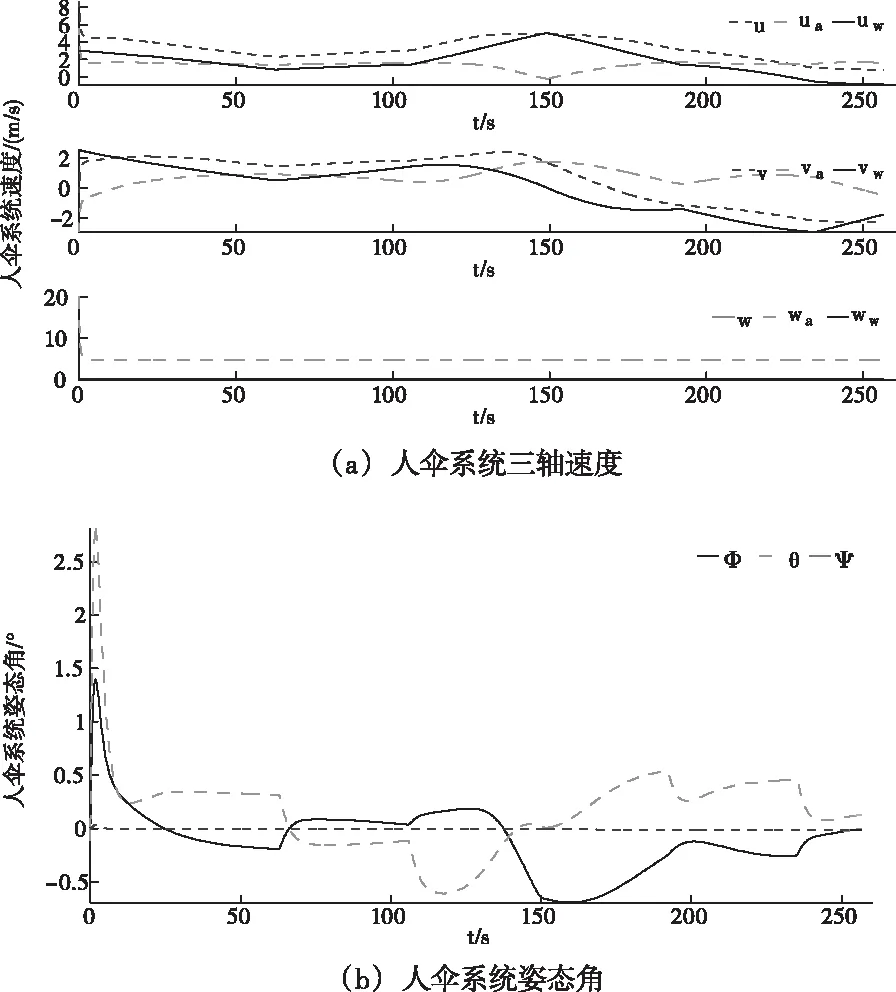
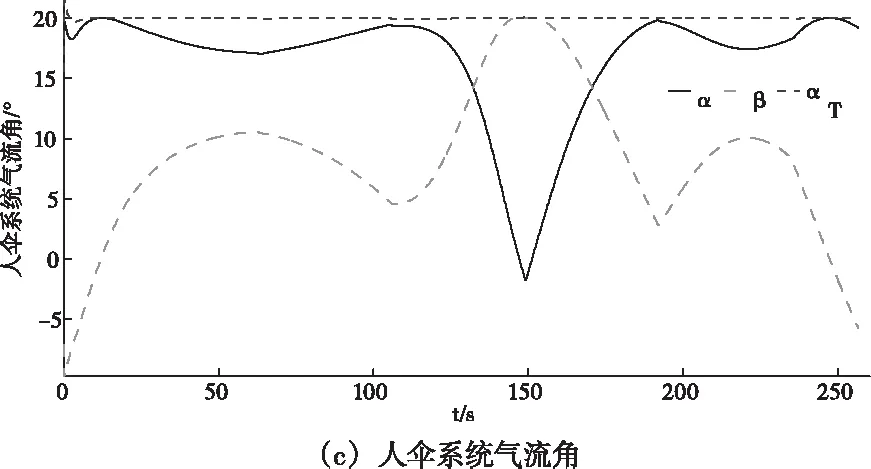
图6 平均风扰动下的仿真曲线

另外，由图6()可以看到，系统姿态角在平均风扰动下，变化幅度比较稳定，滚转角与俯仰角都保持在近05°的范围内，表明平均风对系统姿态影响的绝对尺度很小，可以不予考虑。而图6()表明，平均风场主要通过改变人伞系统迎角与侧滑角以改变运动轨迹，但其总攻角几乎保持不变，对风速的改变并不敏感。

图7～8为紊流扰动下系统运动状态，可以看到，相对于平均风场，紊流由于更快的风速变化频率，对伞降轨迹的影响更加明显，在降落过程中，系统出现水平方向多次的变向运动，不利于跳伞员准确判断预定降落区域，规避地面危险物体。另外，相较于平均风场，紊流扰动下系统姿态角的变化也呈现较大震幅，使降落伞运动形式变得不太规则，对伞降过程系统的稳定操纵提出了挑战。

图7 伞降三维轨迹图

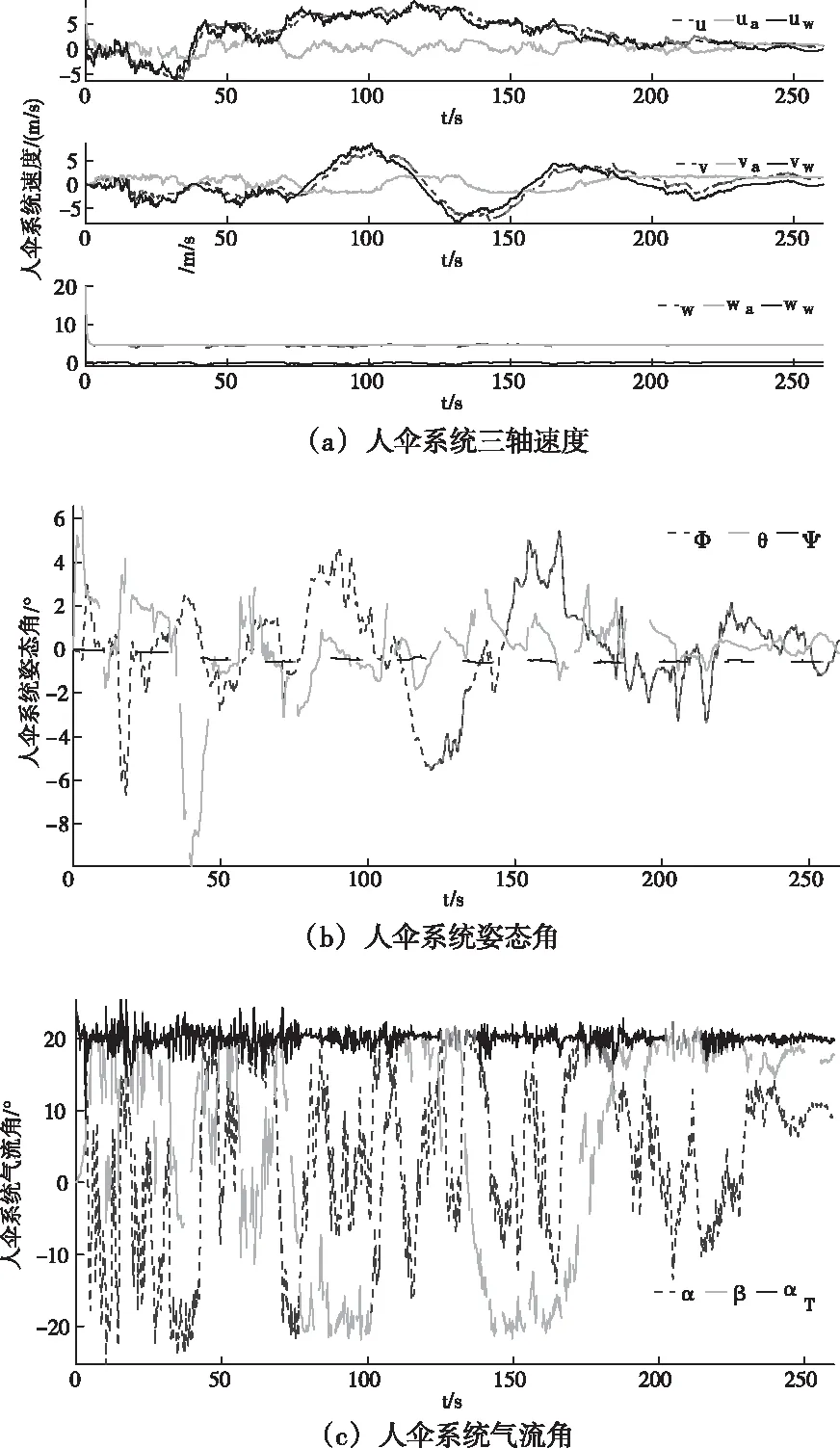
图8 紊流扰动下的仿真曲线

3.3 跳伞员操纵的仿真结果

通过前面的仿真可以看到，风场扰动对伞降轨迹影响较大，为了准确降落至预定区域，必须在伞降过程中施加相应操纵，本节以平均风扰动条件为例，经过反复调试，分别当=68-69和=74-76时输入操纵值为==1，=191-194和=200-202时输入操纵值为==1，可使人伞系统降落至预定区域，仿真结果如图9～10所示。

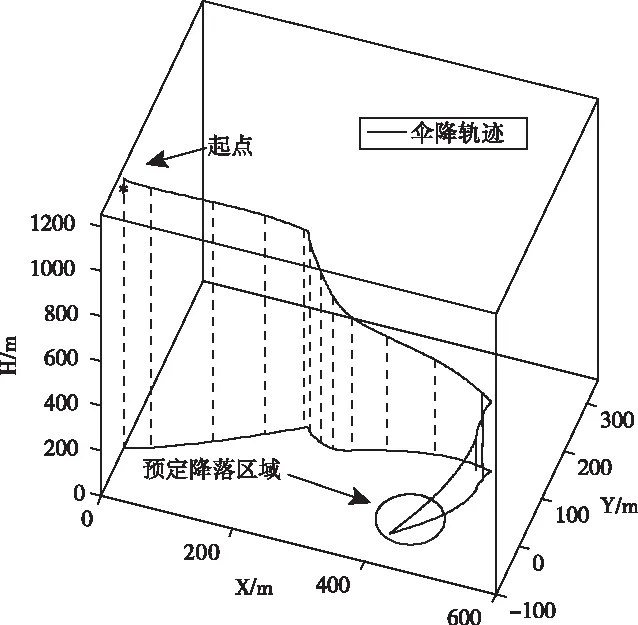
图9 伞降三维轨迹图

图10 平均风场操纵伞降的仿真曲线

首先，仿真结果表明通过合适的操纵输入，人伞运动轨迹可被控制在理想范围内，另外，在进行操纵方式选择仿真过程中发现，少量多次的操纵比长时间单次的操纵操纵效果更佳，这个结果也与人用伞操纵手册相符，原因可以通过分析图10()的气流角得到：当操纵动作发生后，首先改变人伞系统平衡攻角的方向，进而改变降落伞气动力与力矩，而在操纵开始的较短时间内，系统力与力矩快速达到平衡状态，导致长时间的单一操纵并不会产生长时间的操纵效果。

人伞运动过程的操纵组合较多，本节仅以进入预定降落范围为目标进行试错调试，操纵方法与实际过程有较大区别，但仿真结果也表明，本文所建立的六自由度运动模型符合实际人伞系统运动过程，可以有效模拟伞降过程，在将本模型嵌入跳伞模拟器后，跳伞员可在实时获得模型运动状态值后，通过平时训练中讲授的操纵方法应对不同情况，以获得预定降落轨迹和着陆姿态。更进一步，本文所建立模型也可通过建立反馈控制机制，得到不同初始条件、不同扰动条件下跳伞员应采取的最佳操纵组合，这也是下一步的研究重点。

4 结论

本文针对跳伞模拟器动力学建模需求，给出了人伞系统六自由度运动的数学模型。该模型综合考虑伞降过程风场扰动与跳伞员控制输入，增加了四种操纵方法，通过数值仿真的方法分析复杂大气扰动对伞降过程的影响，可以提供跳伞模拟器所需的输出。建立的模型贴近伞降实际，为综合运用数值仿真、半实物仿真的方法研究伞降模拟奠定了理论基础，可为部队官兵和军校学员的跳伞训练提供一种新的途径。