r-正则模糊图的运算及其性质

更芷拉毛，索南仁欠

(1.青海师范大学 数学与统计学院，青海 西宁 810016；2.青海师范大学 研究生院，青海 西宁 810008)

基于模糊集理论，Rosenfeld于1975年提出了模糊图，建立了模糊图的理论结构.随后许多学者对模糊图进行了深入细致的研究，定义了模糊图的强积、直积和字典乘积等运算,并总结出了模糊图乘积运算相关的分解定理和同构定理.本文将定义r-正则模糊图的交、并、补、笛卡尔积、直积、强乘积、字典乘积运算，并探讨r-正则模糊图在以上运算下是否满足封闭性等相关的性质.

1 预备知识

定义1.1[1]对于任意给定的集合V，在V×V-{(x，x)|x∈V}上定义等价关系～如下：

(x1，y1)～(x2，y2)⟺(x1，y1)=(x2，y2)或者(x1，y1)=(y2，x2).

定义1.2[1]称任意映射A：V→[0，1]为V上的模糊集.suppA={x∈V|A(x)>0}(称为A的承载集)，rangA={A(x)|x∈V}(称为A的值域).

定义1.4[3]模糊图是一个有序三元组G=(G*，σ，μ)(更多时候为了方便G*略去不写)，其中G*=(V，E)是一个无向简单图，称为基图.σ：V→(0，1]，μ：E→(0，1]，且∀e∈E，μ(e)≤σ(u)∧σ(v)，这里u，v是e的端点.

定义1.5[4]若X的两个模糊集μ和τ满足μ(x)≤τ(x)(∀x∈X)，则记μ≤τ.若两个模糊图H=(σ1，μ1)和G=(σ，μ)满足σ1≤σ和μ1≤μ，则称H是G的偏模糊子图.

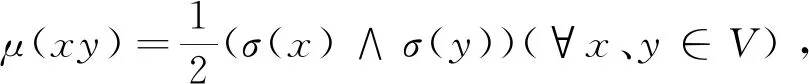
定义1.8[6]模糊图G=(σ，μ)中点u的度数(degree)为dG(u)=∑uv∈Eμ(uv)(∀u∈V).

定义1.9[7]设G=(σ，μ)是以图G*=(V，E)为基图的一个模糊图，如果dG(v)=r(∀v∈V，r>0)，即G中所有顶点的度数为r，则称G为一个r-正则模糊图(r-regularfuzzygraph).

定义1.10[8]设G=(σ，μ)是以图G*=(V，E)为基图的模糊图，对∀e∈E，μ(e)=σ(u)∧σ(v)(这里u，v是e的端点)，则称G=(σ，μ)为强模糊图.

2 主要结果

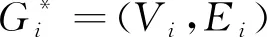
其中:σ1∩σ2：V1∩V2→(0，1]，μ1∩μ2：E1∩E2→(0，1].

具体定义为：

(σ1∩σ2)(v)=σ1(v)∧σ2(v)(∀v∈V1∩V2)，

(μ1∩μ2)(e)=μ1(e)∧μ2(e)(∀e∈E1∩E2).

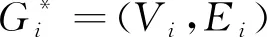
证明：设Gi为ri-正则模糊图(i=1，2)，μi(e)=Ci(∀e∈Ei)，C1、C2为常数.

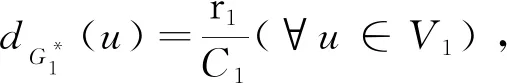
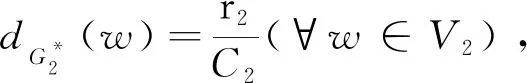
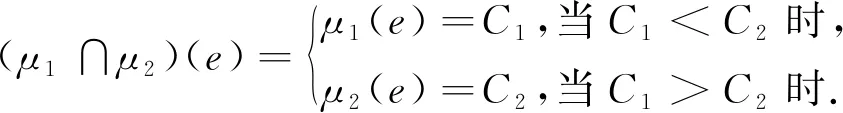
设(G1∩G2)*为r-正则图，则对于任意的v∈V1∩V2有

因此G1∩G2为正则模糊图.

反之，设G1∩G2=(σ1∩σ2，μ1∩μ2)为正则模糊图，V1∩V2中任取两点v和w，有

dG1∩G2(v)=dG1∩G2(w)

⟹C1·d(G1∩G2)*(v)=C1·d(G1∩G2)*(w)

⟹d(G1∩G2)*(v)=d(G1∩G2)*(w)(当C1≤C2时)

或C2·d(G1∩G2)*(v)=C2·d(G1∩G2)*(w)

⟹d(G1∩G2)*(v)=d(G1∩G2)*(w)(当C1>C2时)

由于v和w在V1∩V2中的任一性，(G1∩G2)*为正则图.

推论2.1 设G=(σ，μ)是以图G*=(V，E)为基图的模糊图，若μ为常值函数且G*为正则图，则G=(σ，μ)为正则模糊图.

命题2.1 设Gi=(σi，μi)是ri-正则模糊图(i=1，2).若G2为G1的偏模糊子图，则G1∩G2为r2-正则模糊图.

证明：G2为G1的偏模糊子图，则σ1与σ2为非空结点集V上的两个模糊集，且有σ2(x)≤σ1(x)(∀x∈V)和μ2(xy)≤μ1(xy)(∀x，y∈V)，则：

(σ1∩σ2)(x)=σ2(x)(∀x∈V)，(μ1∩μ2)(xy)=μ2(xy)(∀xy∈E)

故有G1∩G2=(σ1∩σ2，μ1∩μ2)=(σ2，μ2)=G2,因此G1∩G2为r2-正则模糊图.

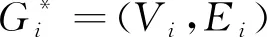
其中:σ1∪σ2：V1∪V2→(0，1]，μ1∪μ2：E1∪E2→(0，1].

具体定义为：

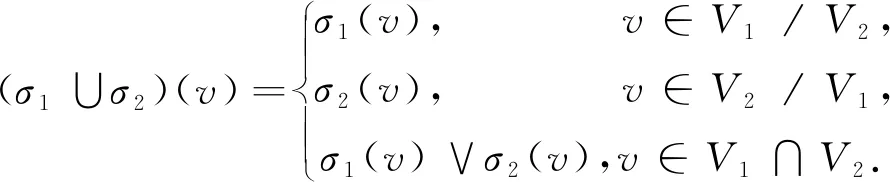
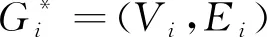
证明：设Gi为ri-正则模糊图，μi(uv)=(μ1∪μ2)(uv)=C(∀uv∈Ei，C为常数，i=1，2).

设(G1∪G2)*为r-正则图，任取v∈V1∪V2，

因此G1∪G2为正则模糊图.

反之，设G1∪G2为正则模糊图，V1∪V2中任取两点v和w，有

dG1∪G2(v)=dG1∪G2(w)

⟹C·d(G1∪G2)*(v)=C·d(G1∪G2)*(w)

⟹d(G1∪G2)*(v)=d(G1∪G2)*(w)

由于v和w在V1∪V2的任一性，(G1∪G2)*为正则图.

命题2.2 设Gi=(σi，μi)是ri-正则模糊图(i=1，2).若G2为G1的偏模糊子图，则G1∪G2为r1-正则模糊图.

证明：G2为G1的偏模糊子图，则σ1与σ2为非空结点集V上的两个模糊集，且有σ2(x)≤σ1(x)(∀x∈V)和μ2(xy)≤μ1(xy)(∀x，y∈V)，则:

(σ1∪σ2)(x)=σ1(x)(∀x∈V)，(μ1∪μ2)(xy)=μ1(xy)(∀xy∈E)，

故G1∪G2=(σ1∪σ2，μ1∪μ2)=(σ1，μ1)=G1

因此G1∪G2为r1-正则模糊图.

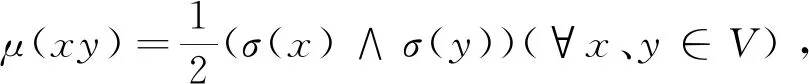
具体定义为：

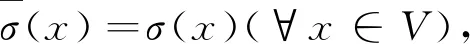
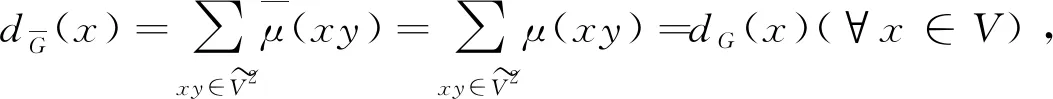
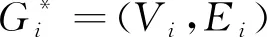
其中:

σ1×σ2：V1×V2→(0，1]，μ1×μ2：E→(0，1];

E={(x，x2)(x，y2)|x∈V1，x2y2∈E2}∪{(x1，z)(y1，z)|z∈V2，x1y1∈E1}.

具体定义为：

(σ1×σ2)(x1，x2)=σ1(x1)∧σ2(x2)(∀(x1，x2)∈V1×V2);

(μ1×μ2)((x，x2)(x，y2))=σ1(x)∧μ2(x2y2)(∀(x，x2)(x，y2)∈E);

(μ1×μ2)((x1，z)(y1，z))=σ2(z)∧μ1(x1y1)(∀(x1，z)(y1，z)∈E).

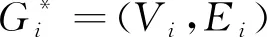
证明：设σ1(v)=C1(∀v∈V1)，σ2(u)=C2(∀u∈V2)，C1、C2为常数.|V1|=n，|V2|=m.

任取一点(x1，x2)∈V1×V2，

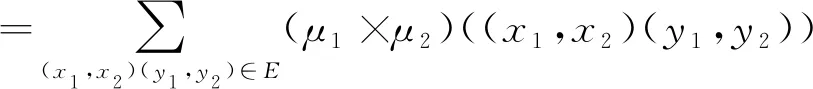
=∑x1=y1∈V1，x2y2∈E2σ1(x1)∧μ2(x2y2)+∑x2=y2∈V2，x1y1∈E1σ2(x2)∧μ1(x1y1)

当σ1≥σ2时，dG1×G2((x1，x2))=∑x2y2∈E2μ2(x2y2)+∑x1y1∈E1σ2(x2) (σ1=μ1，σ2=μ2)

=C2·(m-1)+C2·dG1*(x1)

=C2·(m+n-2).

当σ2>σ1时，dG1×G2((x1，x2))=∑x2y2∈E2σ1(x1)+∑x1y1∈E1μ1(x1y1) (σ1=μ1，σ2=μ2)

=C1·dG2*(x2)+C1·(n-1)

=C1·(m+n-2).

因此G1×G2为正则模糊图.

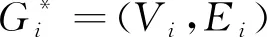
其中：

σ1*σ2：V1×V2→(0，1]，μ1*μ2：E°→(0，1]；

E°={(x1，x2)(y1，y2)|x1y1∈E1，x2y2∈E2}.

具体定义为：

(σ1*σ2)(x1，x2)=σ1(x1)∧σ2(x2)(∀(x1，x2)∈V1×V2，)

(μ1*μ2)((x1，x2)(y1，y2))=μ1(x1y1)∧μ2(x2y2)∀(x1，x2)(y1，y2)∈E°.

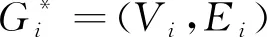
证明：设(G1*G2)*为p-正则图，μ1与μ2为常值函数，μ1(xy)=C1(∀xy∈E1)，μ2(xy)=C2(∀xy∈E2)，C1与C2为常数.

任取(x1，x2)∈V1×V2，

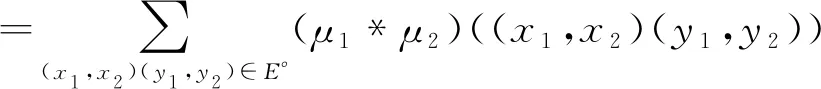
=∑x1y1∈E1，x2y2∈E2μ1(x1y1)∧μ2(x2y2)

当μ1≥μ2时，dG1×G2((x1，x2))=∑(x1，x2)(y1，y2)∈E°μ2(x2y2)

=C2·d(G1*G2)*(x1，x2)=C2·p

当μ1<μ2时，dG1×G2((x1，x2))=∑(x1，x2)(y1，y2)∈E°μ1(x1y1)

=C1·d(G1*G2)*(x1，x2)=C1·p

因此G1*G2为正则模糊图.

反之，设G1*G2为正则模糊图，任取两点(x1，x2)、(z1，z2)∈V1×V2，有

dG1*G2((x1，x2))=dG1*G2((z1，z2))

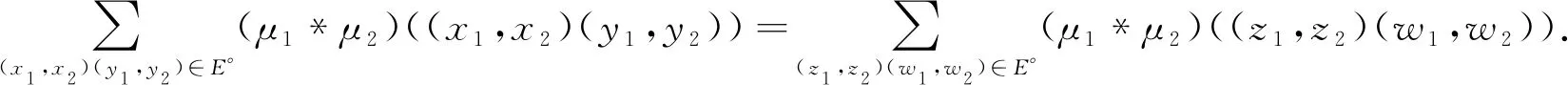
当μ1≥μ2时，有

⟹C2·d(G1*G2)*(x1，x2)=C2·d(G1*G2)*(z1，z2)

所以d(G1*G2)*(x1，x2)=d(G1*G2)*(z1，z2)

当μ1<μ2时，有

⟹C1·d(G1*G2)*(x1，x2)=C1·d(G1*G2)*(z1，z2)

所以d(G1*G2)*(x1，x2)=d(G1*G2)*(z1，z2)

由于(x1，x2)和(z1，z2)在V1×V2中的任一性，(G1*G2)*为正则图.

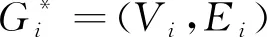
其中:

σ1⊗σ2：V1×V2→(0，1]，μ1⊗μ2：E。→(0，1].

E。=E∪E°，E和E°分别在定义2.5和定义2.6中给出.

具体定义为：

(σ1⊗σ2)(x1，x2)=σ1(x1)∧σ2(x2)(∀(x1，x2)∈V1×V2),

(μ1⊗μ2)((x，x2)(x，y2))=σ1(x)∧μ2(x2y2)(∀(x，x2)(x，y2)∈E),

(μ1⊗μ2)((x1，z)(y1，z))=σ2(z)∧μ1(x1y1)(∀(x1，z)(y1，z)∈E),

(μ1⊗μ2)((x1，x2)(y1，y2))=μ1(x1y1)∧μ2(x2y2)(∀(x1，x2)(y1，y2)∈E°).

根据模糊图的定义，对所有xy∈Ei，i=1，2有μi(xy)≤σi(x)∧σi(y)，因此μi≤maxσi和minμi≤σi，i=1，2.因为σ1≤μ2，maxσ1≤minμ2，因此μ1≤maxσ1≤minμ2≤σ2即σ2≥μ1.

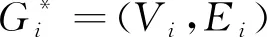
证明：设(G1*G2)*为p-正则图，Gi为ri-正则模糊图(i=1，2)，μ1与μ2为常值函数，则μ1(xy)=C1(∀xy∈E1)，μ2(xy)=C2(∀xy∈E2)，C1与C2为常数.

任取(x1，x2)∈V1×V2，

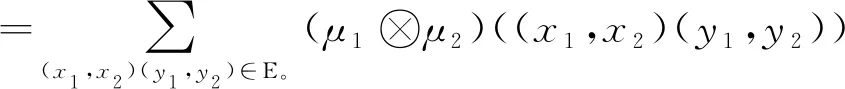
=∑(x1，x2)(y1，y2)∈E(μ1⊗μ2)((x1，x2)(y1，y2))+∑(x1，x2)(y1，y2)∈E°(μ1⊗μ2)((x1，x2)(y1，y2))

=∑x1=y1∈V1，x2y2∈E2σ1(x1)∧μ2(x2y2)+∑x2=y2∈V2，x1y1∈E1σ2(x2)∧μ1(x1y1)+∑x1y1∈E1，x2y2∈E2μ1(x1y1)∧μ2(x2y2)

当μ1≤μ2时，dG1⊗G2((x1，x2))=∑x2y2∈E2μ2(x2y2)+∑x1y1∈E1μ1(x1y1)+∑(x1，x2)(y1，y2)∈E°μ1(x1y1)

=dG2(x2)+dG1(x1)+C1·d(G1*G2)*(x1，x2)=r2+r1+C1·p;

当μ1>μ2时，dG1⊗G2((x1，x2))=∑x2y2∈E2μ2(x2y2)+∑x1y1∈E1μ1(x1y1)+∑(x1，x2)(y1，y2)∈E°μ2(x2y2)

=dG2(x2)+dG1(x1)+C2·d(G1*G2)*(x1，x2)=r2+r1+C2·p,

因此G1⊗G2为正则模糊图.

反之，设G1⊗G2为正则模糊图，则任取两点(x1，x2)、(z1，z2)∈V1×V2，有

dG1⊗G2((x1，x2))=dG1⊗G2((z1，z2))

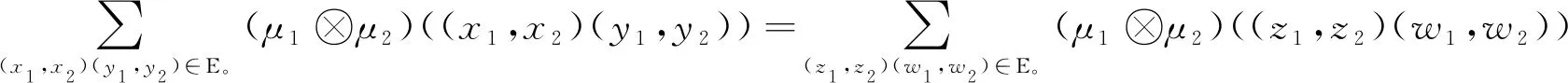
当μ1≤μ2时，有

dG2(x2)+dG1(x1)+C1·d(G1*G2)*(x1，x2)=dG2(z2)+dG1(z1)+C1·d(G1*G2)*(z1，z2)

r2+r1+C1·d(G1*G2)*(x1，x2)=r2+r1+C1·d(G1*G2)*(z1，z2)

d(G1*G2)*(x1，x2)=d(G1*G2)*(z1，z2)

当μ1>μ2时，有

dG2(x2)+dG1(x1)+C2·d(G1*G2)*(x1，x2)=dG2(z2)+dG1(z1)+C2·d(G1*G2)*(z1，z2)

r2+r1+C2·d(G1*G2)*(x1，x2)=r2+r1+C2·d(G1*G2)*(z1，z2)

d(G1*G2)*(x1，x2)=d(G1*G2)*(z1，z2)

由于(x1，x2)和(z1，z2)在V1×V2中的任一性，(G1*G2)*为正则图.

定义2.8 设G=(σ，μ)是以图G*=(V，E)为基图的一个r-正则模糊图.若∀e∈E，μ(e)=σ(u)∧σ(v)，这里u，v是e的端点，则称G=(σ，μ)为强r-正则模糊图.

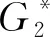
任取(x1，x2)∈V1×V2，

=∑(x1，x2)(y1，y2)∈E(μ1⊗μ2)((x1，x2)(y1，y2))

+∑(x1，x2)(y1，y2)∈E°(μ1⊗μ2)((x1，x2)(y1，y2))

=∑x1=y1∈V1，x2y2∈E2σ1(x1)∧μ2(x2y2)+∑x2=y2∈V2，x1y1∈E1σ2(x2)∧μ1(x1y1)

+∑x1y1∈E1，x2y2∈E2μ1(x1y1)∧μ2(x2y2)

=∑x2y2∈E2σ1(x1)+∑x1y1∈E1μ1(x1y1)+∑(x1，x2)(y1，y2)∈E°μ1(x1y1)

=C1·p+r1+C1·q

因此同理可得:G1⊗G2为正则模糊图.

其中:

σ1∘σ2：V1×V2→(0，1]，μ1∘μ2：E。∪E′→(0，1].

E。在定义2.7中给出，E′={(x1，x2)(y1，y2)|x1y1∈E1，x2y2∉E2},

具体定义为：

(σ1∘σ2)(x1，x2)=(σ1⊗σ2)(x1，x2)(∀(x1，x2)∈V1×V2)，

(μ1∘μ2)((x1，y1)(x2，y2))=(μ1⊗μ2)((x1，y1)(x2，y2))(∀(x1，y1)(x2，y2)∈E。)，

(μ1∘μ2)((x1，y1)(x2，y2))=μ1(x1，x2)∧σ2(y1)∧σ2(y2)(∀(x1，y1)(x2，y2)∈E′).

E′={(x1，x2)(y1，y2)|x1y1∈E1，x2y2∉E2}=Ø.

所以G1∘G2=G1⊗G2.