基于PM模型的改进SIRT图像重建算法
梁 婕
(山西师范大学临汾学院,山西 临汾 041000)
0 引言
计算机断层成像(Computed Tomography,CT)技术,是一门利用X射线穿透物体的衰减信息进行重建来获取物体的短促图像信息的技术,它被公认为20世纪后期最伟大的科技成果之一.CT技术的核心是CT图像重建,其特点是可以在不对物体造成任何的物理性损伤的基础上,获取被检测物体内部结构的图像.目前已广泛应用于工业无损检测、医学诊断、农林业、地球物理等领域[1].
CT图像重建算法大致可以分为以Radon变换为理论基础的解析类重建算法和以解方程为主要思想的迭代类重建算法两大类.解析法是以滤波反投影算法(Filtered Back Projection,FBP)为主,优点是运算速度快,但其抗噪声性能差,对投影数据的完备性要求较高.联立迭代重建算法(Simultaneous Iterative Reconstruction Technique,SIRT)是迭代重建中典型的算法之一,其优势在于对数据的完备性要求不高,缺点是计算量大,重建速度慢,难以用硬件实现[2].近年来,计算机技术的发展十分快速,这使得SIRT算法的缺点已成为次要矛盾,其优势更加突出,人们更为关注的是如何提高该算法的重建质量.
在实际应用中,由于投影数据的不完备或者存在着噪声,使得图像重建的效果并不明显,继而给一些后继的图像处理,如特征提取、图像分割、边缘检测等带来许多困难.因此,需要通过对图像进行去噪处理来提高图像重建的质量.近年来,偏微分方程(PDE)方法已广泛应用于图像去噪,在噪声消除和与边缘保留方面取得了较好的效果,其中较为常用的去噪模型是PM模型[3].1990年,Perona 和Malik 提出了经典的非线性扩散模型.基于SIRT重建算法,本文利用PM模型的去噪原理,分析了该模型的优缺点并对其扩散系数进行了改进,给出了一种新的迭代重建算法,记作PM-SIRT算法.仿真实验结果验证了该算法的有效性.
1 背景知识
1.1 迭代重建算法原理
与解析法不同,迭代重建算法是在离散域中进行的.把图像重建区域划分为一个n×n的正方形网格,且每个网格(像素)内f为常数,这样就可以建立一个线性方程组来描述像素与投影数据之间的关系,从而把图像重建问题转化成为解该方程组[4].
(1)
式中:每一个方程代表一个超平面,pi表示第i条射线的投影值,fj表示第j个网格内的常量,wij代表权因子,反映了第j个像素对第i条射线投影值的贡献,N(N=n×n)代表像素总数.在实际应用中,为提高重建速度,减少计算量,对wij简化,假设像素宽度等于射线宽度,像素值集中在像素的中心,当射线穿过像素中心时,权因子定义为1,即
(2)
式(1)可以用矩阵形式表示为:
WF=P
(3)
式中:W为M×N维投影系数矩阵;F为N维图像向量;P为M维投影数据向量.如何利用W和P求出F是图像重建的任务,这样就将图像重建问题转化为求解一个大型线性方程组的问题.
1.2 SIRT算法
在实际应用中,因为投影矩阵W非常庞大,求取图像F时,一般不直接用M×N维矩阵的逆矩阵运算.随后,由WF=P推导出了ART算法,且Gilbert于1972 年提出了改进技术联立迭代重建算法(SIRT).在SIRT算法中,一个像素的平均修正值是通过利用这一像素内通过的所有射线修正值来确定,这样可以平滑噪声,相比于ART算法,SIRT能够使重建图像更加平滑,更好地压制带状伪影.SIRT算法的迭代公式为:
(4)
式中:λ为松弛因子(0<λ<2),且λ的选取根据投影数的多少和噪声的大小而有所不同.在迭代过程中,需要寻求适当的λ来提高收敛速度和重建质量[5].
在方程组(1)中,每一个方程表示一个超平面.每按照式(4)进行一次迭代,表示要利用所有的射线对某些像素值进行修正,每修正一次即对重建图像更新一次,不断地对图像进行校正,直到满足所需要求,然后结束迭代过程.
2 非线性扩散模型
2.1 PM模型
由Perona和Malik提出的非线性扩散模型—PM模型[4],是一种常用的去噪方法,表达式如下:
(5)
式中:div为散度算子;∇为梯度算子;∇u=[ux,uy]T;|∇u|表示图像梯度的模;c(·)为扩散系数;u0为原始图像;t为时间变量.

c1(|∇u|)=1/1+(|∇u|/k)2
(6)
c2(|∇u|)=exp[-(|∇u|/k)2]
(7)
式中:k为扩散门限,且该参数的大小由具体的应用情况确定,k越大,平滑的力度就越大.
根据扩散系数c(·)的性质可知,在|∇u|较小的均匀区域,为了去除噪声,对图像的平滑作用应增强;而在|∇u|较大的边缘附近,对图像的平滑作用应“停止”,以保护边缘细节信息.
2.2 PM模型的优缺点分析
PM模型是一种基于PDE的非线性扩散模型,在对图像去噪的过程中,有以下2个优点[6-7]:
① 保留边缘细节.在边缘附近所对应的c(·)趋于0,扩散速度较低,故在边缘附近,平滑之前像素的灰度值对平滑之后的影响很小.因此,利用PM模型去噪可以保护图像的边缘.
② 平滑图像噪声.在均匀区域内所对应的c(·)趋于1,扩散速度较高,故该区域内的像素值做一次平滑后,对图像的影响不大.因此,对于含有噪声的像素点,利用PM模型可以进行有效地平滑.
PM模型有以下3个缺点[6-7]:
① 有零散斑点的出现.因为PM模型在去除均匀区域内的孤立噪声点时,会把它们误认为图像的边缘而予以保留,这就使得去噪后的图像中有零散的斑点出现.
② 平滑效果一般.若像素p是一个孤立的噪声点,如果该点与邻域中每个像素q相比,都有较大的灰度值差距,那么对应的梯度一定很大,使得扩散速度降低,不利于去除该点的孤立噪声.
③ 扩散系数是病态的.因为c(·)是趋向于0,但达不到0,所以给出的扩散系数式(6)和式(7)是病态的,也就是说在图像的边缘附近,即使|∇u|很大,但由于c(·)≠0,使得这些像素依然会受到邻域像素的影响.尽管影响很小,但是随着迭代次数的增加会被放大,这就会模糊甚至是破坏图像的边缘细节.
对于PM模型所存在的问题,为了更好地降噪和保持边缘细节能力,需对PM模型进行改进.
2.3 PM模型的改进
本文中,针对PM模型去噪时会有零散斑点出现、平滑效果一般的缺点,结合Catté_PM模型的特点,通过引进高斯算子Gσ来实现.也就是说利用Gσ对噪声图像进行高斯平滑,即Gσ*u,这就大大降低了孤立噪声点处的邻域像素对其梯度的影响,且增大扩散系数,有利于对孤立噪声点的去除.
其次,针对扩散系数c(·)是病态的问题,本文通过对c(·)进行改进,构造出一个新的扩散系数:
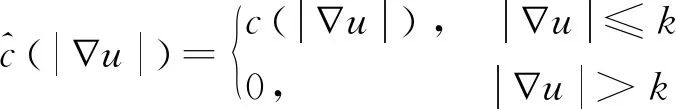
(9)
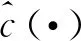
综上所述,改进后的PM模型可表示为:
(10)
3 PM-SIRT重建算法
由于传统的SIRT算法并不能去除投影数据及重建图像中的噪声[8],故本文提出了一种改进算法,主要是将图像去噪与图像重建相结合,在SIRT算法每次迭代后,利用PM模型对重建图像去噪,使得SIRT算法与PM模型可以循环交替进行.该算法的具体步骤如下:
①对投影数据P进行加噪处理;
②初始化各参数,令F0=0,设定初始迭代值j=1和最大迭代次数maxiter;
③利用初始值F0及投影数据P进行SIRT迭代,得到重建图像Fj;
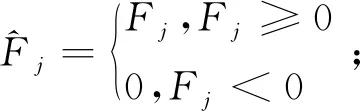
⑥j=j+1:若j≤maxiter,返回步骤③继续进行迭代,直到满足停止迭代条件.
4 仿真实验结果与分析
为了验证PM-SIRT算法的有效性,仿真实验中使用180*180的Shepp-Logan模型进行图像重建,如图1所示.本文中,针对投影数据中加入高斯白噪声(均值为0,标准差分别为0.5和1)的情况进行仿真.其中,设定最大迭代次数maxiter=10,σ=5,通过反复实验、对比,选取参数k=20.
图2给出了SIRT、SIRT+PM和PM-SIRT算法所重建的图像,其中SIRT+PM算法的具体流程与PM-SIRT算法一致,但其扩散系数选用式(7).
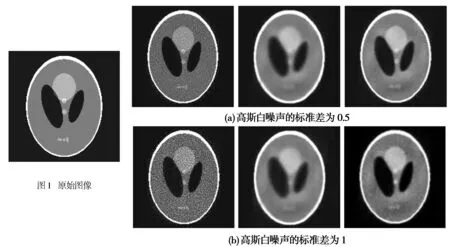
图2 三种算法的重建图像(从左到右依次为SIRT算法,SIRT+PM算 法和PM-SIRT算法
从图2可以看出,在加入标准差为0.5和1的高斯白噪声的情况下,相比于SIRT+PM算法、SIRT算法,PM-SIRT算法能够有效地减少了噪声和伪影且平滑性较好,重建出的图像与原始图像更加接近.
三种算法所重建出的图像在第90列的密度曲线如图3所示,其中图3(a)为高斯白噪声的标准差为0.5时的密度曲线,图3(b)为高斯噪声的标准差为1时的密度曲线.由此可见,本文算法的重建质量优于SIRT+PM算法和SIRT算法.
为了进一步比较三种算法的重建效果,本文中利用均方误差(MSE)、信噪比(SNR)和峰值信噪比(PSNR)来评估重建图像的质量,衡量重建图像和原始图像的逼近程度,计算结果如表1所示.

图3 3种算法的密度曲线图

表1 三种量化评估

续表
由表1可以看出,PM-SIRT算法的MSE最小,而SNR和PSNR最大.表明本文算法的重建效果较好,更加逼近Shepp-Logan模型图像.
5 结束语
基于PM模型的优缺点分析,本文提出了改进方法,构造一个新的扩散系数,将SIRT算法与PM模型相结合,使之循环交替进行,从而给出了基于PM模型的改进SIRT图像重建算法.实验结果表明,本文算法的信噪比和峰值信噪比更高,误差更小,进一步提高了重建图像的质量,有效地减少了噪声对图像的影响,使重建图像更加逼近于原始图像,获得较好的视觉效果图.

