基于数据发现的同心鼓协同模型若干问题研究

周 蔷

(湘南学院 经济管理学院 物流系,湖南 郴州 423000)

1 问题概述

本文主要探究根据题目中提供的数据信息，对整个同心鼓拓展项目进行数据可视化的物理分析.总的来说，一共要解决四个问题：

问题一：首先利用恢复系数的经典力学接触模型，求出碰撞过程中的能量损失ΔE.其次再根据基于线性阻尼的动态接触模型，求出整个接触过程中接触力所作的功W(即为能量损失)，再根据ΔE=W解出接触阻尼系数cn.最后，我们建立了计算鼓与球撞击过程中速度衰减的复杂物理模型，通过Simulink系统仿真计算出球碰撞鼓面后速度恢复至碰撞前一刻的速度相同耗时0.22s，再通过计算所需合力的大小所得排球反弹时初速度为2.8m/s时，竖直方向上的合力为82.7N.最终解出排球弹起的最佳高度为40cm.

问题二：由第一问解出当高度为40cm时排球作自由落体运动需要耗时0.29s，利用此条件综合考虑发力力度大小和发力时间对鼓面倾斜角度的影响，分别建立了发力力度大小与倾斜角度关联的复杂物理模型和发力时间对鼓面倾斜角度关联的复杂物理模型，得出水平位移和竖直位移的大小影响鼓面倾斜角度的结论.并最终求得两种模型的倾斜角计算公式.将此倾斜角计算公式代入题目中所提供的9组数据最终求得序号1到序号9所对应的鼓面倾角(度)分别为：5.0976、5.7315、5.2802、4.5416、5.2336、4.9387、8.9904、5.8347、2.0533.

问题三：基于第一问第二问的模型，考虑到倾角的问题，所以对问题一策略改进的结果是：增大竖直方向上的合力，使球的反弹高度增加，在增加的时间内，人做出对鼓面的调整.依据第一问的撞击模型和问题二的倾斜模型，以第二问的数据1作为算例，使小球高度为88.7cm，向上竖直合力为94.78N.

问题四：通过对问题一模型的改进，计算出球的能量损失，使得球水平速度降为0，定义恢复系数e，能量传递率η，得出其均与同心鼓与排球的质量比t和恢复系数e有关.对微分方程求导，t=1时一阶导数为零，二阶导数小于零，为极大值点，η最大.当η达到最大值时，即为10名队员们该发力的时机.

连续颠球的次数受多种因素的影响，比如同心鼓对球的作用力，团队成员对同心鼓的作用力以及球的形变导致鼓的单自由度振动的影响等.主要需要解决的问题如下：

(1)在团队成员可以准确控制力的大小和方向，以及时机的理想条件下，推算出该情形下的最佳协作策略模型，并求出最佳策略下球颠起的高度.

(2)在团队成员不能做到发力时机和力度的精准控制的现实条件下，鼓面与水平面不再平行，即出现了相对于水平地面的倾斜角，在问题二给定的条件下，推算出团队成员的发力时机和力度与鼓面倾斜角度的关系模型.

(3)在该模型中，由于理想条件下的模型和现实条件的模型存在一定的差异，故在现实情形中运用问题一所建立的模型需要进行一定的调整，并给出调整的方案.

(4)由于鼓面的倾斜，球跳动方向也随之倾斜，故需要团队成员调整拉绳使得球调整为竖直的弹跳状态.在问题四给定的条件下，求在理想条件下团队成员的发力时机和力度的调整拉绳模型，以及分析在现实情形条件下调整策略模型的实施效果[1-3].

以下对上述问题进行分析.

对于问题一：该题涉及到很多的物理知识.根据题目可得到的初始条件有：球的高度及其质量、重力加速度g以及同心鼓的质量等，而已知的限制条件主要：有队员的人数、队员之间的最小距离以及球距离鼓面的竖直高度，所以本题的最佳策略的要求是每个队员要用最小的拉力以及考虑其被抵消后，仍能使排球被颠起的最终高度大于40cm.

由于该问题是在理想的状态下进行的，因此每个队员的用力方向、时机和力度是可以根据解答的需要去设定的.当对球进行受力分析时可知，球主要受到各队员沿着绳子向上的作用力，根据物理知识可分析出抵消后的力最终会使球做上升的运动，则可从它的速度和上升的高度进行分析.要解出最佳协作策略，还需要求出绳子的长度以及每个队员的最小用力.

对于问题二：主要涉及到的还是受力分解的知识，即将合力分解为x、y坐标平面上的分力，其合力正好处于z轴上.关于鼓面的倾斜角度问题，首先只需要将8个人的作用力与鼓面的力，平均地分为8个部分(可将每个点视为一个质点)，然后根据每个质点作用力和高度的不同，并且每个质点的高度(即人抓着绳子末端的高度)也可能不同，此时的最高点与最低点的高度差，可以产生倾斜角度.而这个倾斜的角度即为要求的答案.

此外，本问题存在0.1s与-0.1s、0s时刻，并且该问题中指定了初始位置(排球未与鼓面发生碰撞导致鼓面下移)为鼓面相对绳子水平高度下降了11cm，这个时候倘若将鼓面与绳子处于同一平面的话，就会有鼓面上升的阶段，该阶段就具有时刻值的问题.

对于问题三：关于是否要调整的问题，主要分为两个方面：

(1)在所有人用力一致的时候，倘若球尚未达到鼓面时，鼓面就已保持了水平状态，这种情况即无需调整；倘若这种情况下鼓面还没有处于水平状态的话，就需要进行调整.

(2)当所有人用力不一致时，不管球面是否有接触到鼓面，都需要对其进行调整，从而使得鼓面保持水平状态.

在第一问的最佳策略中，只是简单地人数分配以及在假设每个人作用的分力相同的条件下进行的，它成功的最关键的问题在于每个人作用分力的时间是不一致的，这也是解决第三问的关键所在，同时在阐述分析时，也需要对问题一和问题二进行详细地分析，保持内容的完整.

对于问题四：当由于鼓面的倾斜而导致球跳动方向不再竖直时，要找出调整策略，主要的解题思路有：

(1)当鼓面发生了一定程度的倾斜时，鼓面在水平方向上的高度差仍然是确定的，这与问题一的力度的分析是一致的，只是队员人数、绳子的长度以及球反弹的高度有所改变，要求调整拉绳策略的必要的发力时机和力度，可以从问题一建立的模型入手；

(2)由于最优的发力时机和力度是分段进行的，要使倾斜的鼓面在最短的时间内变为水平，则需要每个人力的作用以及发力的时间存在差异性，重点解决的问题是发力的时机以及发力的持续时间，这些都与倾斜后的鼓与水平面的高度差有关；

(3)由于现实情况的不可控性，该调整策略的实施效果可能会出现略差于实验研究的实施效果的情况，可以通过列举特例进行对比.

2 同心鼓协同模型分析

2.1 基本假设

(1)假设忽略空气因素对球的影响；

(2)假设落点为光滑的水平面，不产生摩擦力；

(3)假设在连续颠球的过程中每个人的作用力不会发生突变(避免绳子掉落的情况)；

(4)假设忽略在鼓面震动过程中有外界干扰其震动频率的因素；

(5)假设排球在接触鼓面之后立即产生形变和反弹，过程所有的势能忽略不计；

(6)假设物体发生形变后，不发热、发声，且其形变能够恢复，该过程没有动能损失.

2.2 符号说明

符号名称符号意义va-、va+分别表示a物体碰撞前与碰撞后相对于地面的速度vb-、vb+分别表示b物体碰撞前与碰撞后相对于地面的速度δ接触区域渗透深度,即接触形变δ(0)接触瞬间相对速度en碰撞前后法向相对速度之比rx队员之间的最小距离,其值不得小于60cm

2.3 模型的建立与求解

2.3.1 问题一的模型建立及问题的求解

(1)恢复系数的经典力学接触模型

经典力学接触模型主要使用恢复系数来描述接触碰撞的过程，这是一种对碰撞过程的简化处理方法.模型假设接触过程是在瞬间完成的，物体在碰撞瞬间位置保持不变，速度会发生突变.碰撞过程中，由于碰撞物体的速度是不连续的，无法计算接触力.

古典碰撞理论不考虑碰撞过程中的变形，称作刚性碰撞.对此模型，仅用一个恢复系数来表示碰撞前后的状态，定义碰撞前后法向相对速度之比，其定义为：

(1)

其中：va-、va+、vb-、vb+分别表示为a、b物体碰撞前后相对于地面的速度.根据动能定理，碰撞过程中的能量损失ΔE的关系可表示为：

(2)

将(1)式代入(2)式化简可得：

2.3.2 基于线性阻尼的动态接触模型

动态接触模型可将接触现象作为连续的动力学过程进行处理，能比较简化地求解碰撞过程中各个物理量的时间变化过程.建立合理的碰撞过程模型，是应用动态接触理论的关键.本题主要讨论的是基于线性阻尼模型的动态接触模型，将接触力等效为接触物体之间的弹簧阻尼力.

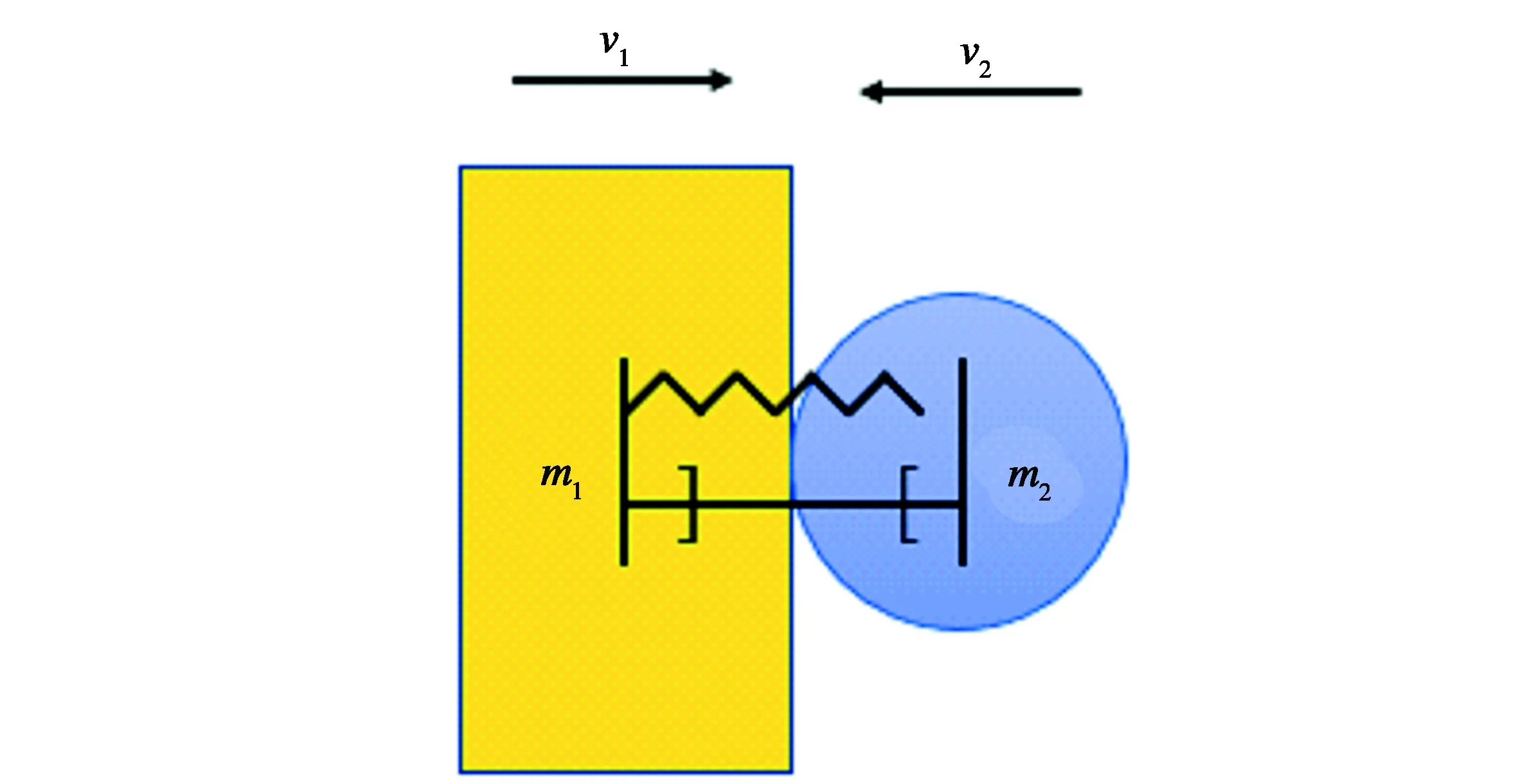
图1 基于线性阻尼模型的动态接触模型图示

由于排球和鼓面形状比较规则且碰撞相对速度不大，根据赫兹接触理论，接触刚度系数与接触物体的材料属性和接触表面的几何形状有关，可得以下计算式：

其中：μ1、μ2、E1、E2、R1、R2分别表示排球和鼓面的材料的泊松比，弹性模量以及曲率半径.

假设当鼓面与排球相接触时，取鼓面曲率半径R2=∞，使用线性阻尼模型模拟接触过程，可将其近似为一个单自由度系统，表示为：

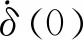
根据ΔE=W，可得阻尼比与恢复系数之间的关系表达式为：

2.3.3 排球的自由下落过程

排球下落的过程中初速度为0，由于速度较低，故其所受的空气阻力数值很小，因此可认为排球只受重力作用，根据动力学公式，有：

根据图2可以得到，各个队员围成的圆环半径计算式为：

其中：rx是队员之间的最小距离，其值不得小于60cm；N是队员的个数，其值最小为8人.

图2 人与鼓的分布图

图3 绳牵引受力分析图

如图3所示：鼓和绳子的牵引位置在鼓的中间H/2处.假设颠球过程中，队员只能抓握绳子的末端，不能接触鼓或绳子的其他位置，因此，人对鼓的拉力是沿着绳子的方向.所以在颠球过程中，相当于鼓与球做相遇运动.对绳子的拉力进行正交分解后，球与鼓碰撞时改变运动双方的运动状态的应为法向方向上的力.可得：

根据牛顿第二定律，得：

F∑y-mbg=mba

F∑x=0

F∑y=N·Fcosφ

F∑y表示绳对鼓在竖直方向的合力，且绳对鼓在水平方向的合力F∑x为0.

2.3.4 模型的建立及求解

由于题目假设每个人都可以精确控制用力方向、时机和力度，而同心鼓项目的目标是使连续颠球的次数最多.那么在理想条件下，如果没有时间限制，连续颠球的次数将会是无限多，然而这样的讨论是没有意义的.所以应假设在单位时间内颠球的次数尽可能多，即为最佳协作方案，换句话也就是说：在单位时间内，降低球颠起的高度来增加颠球的次数，将球弹起的高度设定为达到40cm即可，这样就可以做到在单位时间内颠球次数最多，且是连续颠球[4,5].

(1)鼓与球撞击过程中速度衰减的计算

假设初始位置即鼓最开始摆放的位置，在鼓面与排球碰撞后鼓面下降高度为持球人手部以下11cm，这个高度正好达到鼓的高度的一半.将球的放置高度为40cm，效果如图4所示：

图4 初始位置的确定

同时，设定在鼓面与球相碰撞时，该时刻的碰撞是所在的平面为初始水平面，在此基础上，可设定该水平面为基准面，球的最低高度不能低于基准面上40cm，效果图如图5.

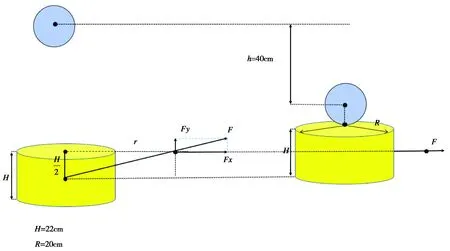
图5 水平面的定义

在此设定的前提上以及上文所做模型的准备，可知小球撞击前初速度，通过Simulink系统仿真计算得可到如下结果(如图6)：

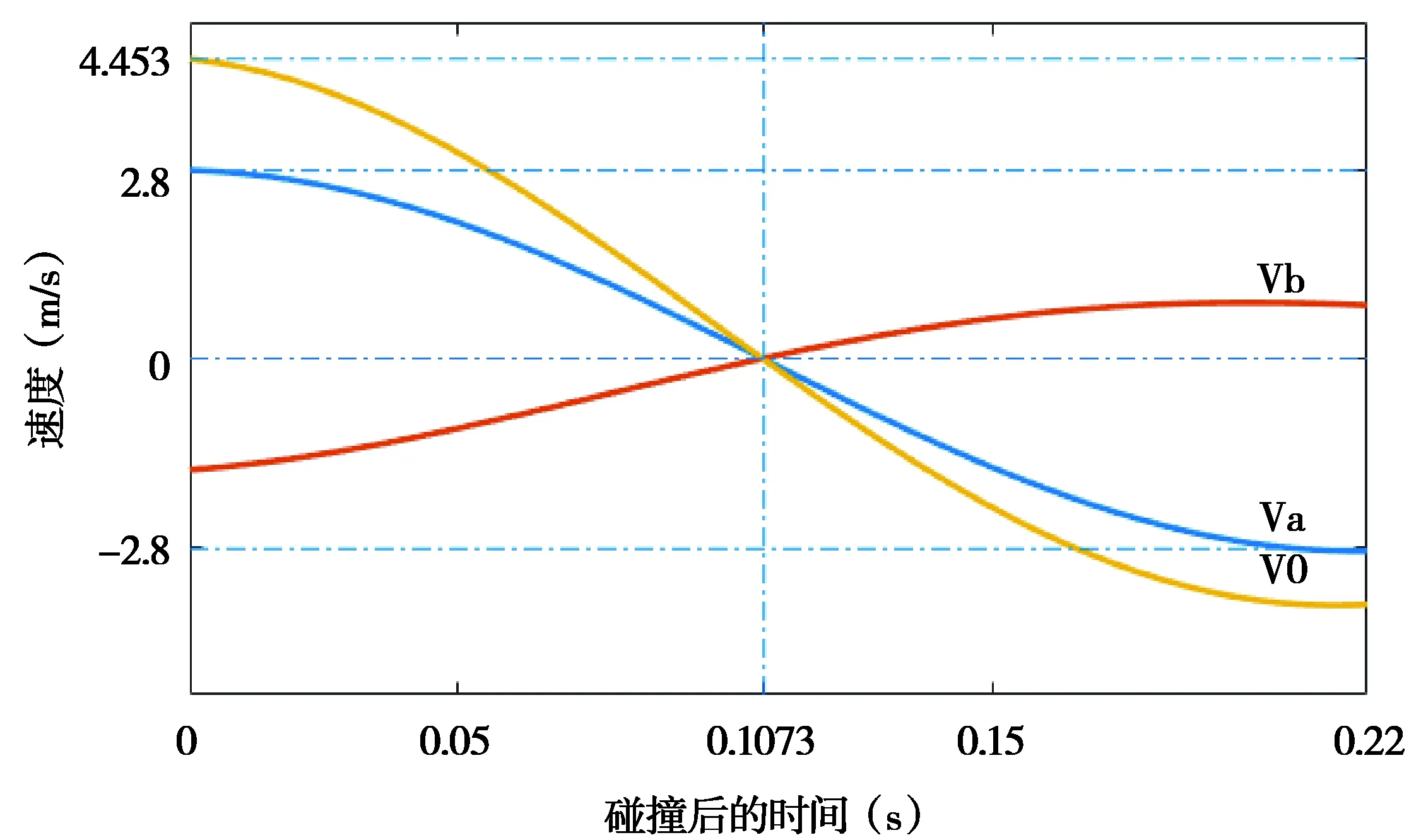
图6 碰撞临界速度图

其中：va表示球的速度，vb表示鼓的速度，v0表示va与vb的相对速度.

如图6所示，该图表示在碰撞过程中，从碰撞开始到碰撞结束的球与鼓的速度变化.由图可知：(1)在碰撞后的0s处，球与鼓的速度分别为2.8m/s，-1.653m/s，速度方向相反.在碰撞过程中，速度不断衰减；(2)在碰撞后0.1073秒处，两物体形变量最大，两物体反向运动，球的速度与初始速度大小相等，方向相反；(3)由于存在人对鼓的拉力作用，最终使鼓做反向的运动，并由于撞击使得能量逐渐衰减.

由于模型本身的不足，动态接触模型计算出的能量为系统损失的总能量，球与鼓接触时均发生弹性形变，且撞击后的两者分别所损失的能量占总损失能量之比无法确定.由于鼓的质量是球的质量的13.33倍，动量差距较大，可以近似认为鼓损失了系统的全部能量，于是球将满足动量守恒定律，最终球恢复速度大小与原来速度相同，整个过程持续0.22s.

(2)计算所需和力的大小

因为假设前提是所有拉绳的人提供相同大小且持续不突变的力，力的方向为沿绳方向，由于所有人位置都对称，那么水平方向上合力始终为零.要使小球弹起高度为40cm，那么小球弹起的速度依然为2.8m/s，方向由竖直向下转变为竖直向上的匀减速直线运动，如图7所示.

图7 竖直方向合力大小与碰撞后排球法量速度的线性关系图

由于我们已知撞击后的速度衰减模型，为了能够使球反弹时初速度为2.8m/s，本文通过Simulink系统仿真模拟图7撞击过程，通过不断施加大小不同的力，得出不同的竖直方向法向的合力作用下，撞击后的球速度变化.经过我们几次模拟仿真得到的数据进行拟合，排球法向速度与竖直方向合力大小呈线性关系.(线性函数式)所以当排球速度为2.8m/s时，竖直方向上的合力为82.7N.

(3)比较准备时间和球体下落时间(模型检验)

由于本问的前提是使高度尽可能小，这样可能会导致当球体下落时间小于鼓提前准备的时间，使球到达预计撞击位置(水平面)时，鼓没有做好准备以相同的位置去撞击球.这样本问的策略将会失败.故本问只需要比较第一次撞击后球回到最高高度即高度为40厘米的时间与鼓回到初始位置的时间作比较.

由动力学方程：

其中：t1为球的运动时间，t为鼓的运动时间，v0为球的初速，v1为鼓的初速.经检验t1大于t2.

2.4 问题二模型建立及问题的求解

分析了排球不考虑空气阻力下的自由落体运动，40cm的距离需要耗时0.29s左右，而在本问题中，需要讨论的是队员们的不同发力时机和力度下，0.1s时的鼓面倾斜角度，因此在该阶段还未涉及到接触碰撞问题.根据运动的合成与分解，在不同的发力时机和力度下，影响鼓面倾斜角度(图8)的是水平位移和竖直位移的大小[5-8].

图8 鼓面斜角的示意图

2.4.1 只考虑发力力度大小对鼓面倾斜角度的影响

在计算鼓面斜角数据时，设1、2、3组数据均为同一时刻发力，相较于所有力均为80N的情况，由于水平方向合力的存在，鼓面会产生倾斜，如图9所示.

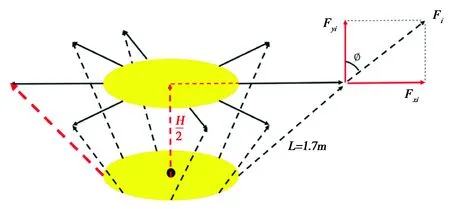
图9 发力力度与倾斜角度示意图

每一个队员施加在鼓面上的水平分量为：

Fxi=Fisinφ

竖直分量为：

Fyi=Ficosφ

F∑y-mbg=mbay

F∑x=mbax

竖直方向位移为：

水平方向位移：

因此，倾斜角的计算公式为：

2.4.2 只考虑发力时机对鼓面倾斜角度的影响

在计算鼓面斜角数据时，设4、5、6组数据均为同样的发力力度，相较于所有力均为80N的同时作用情况，由于某些队员会提前发力，鼓面会产生倾斜.

每一个队员施加在鼓面上的水平分量为：

Fxi=Fisinφ

竖直分量为：

Fyi=Ficosφ

在-0.1s～0s过程中：Fy=mbay1

Fx=mbax1

在0s～0.1s过程中：

F∑y-mbg=mbay2

F∑x=mbax2

竖直方向和水平方向位移由-0.1s～0s和0s～0.1s两部分组成，其中t=0.1s，可得：

(3)

(4)

得倾斜角的计算公式仍为：

(5)

2.4.3 综合考虑发力时机和发力力度大小对鼓面倾斜角度的影响

在计算鼓面斜角数据时，设7、8、9组数据综合考虑了不同的发力时机和发力力度，相较于之前两种情况，综合影响了运动方程里的合力和作用时间，致使竖直方向和水平方向的位移发生变化，有的作用效果会相互抵消，有的会相互叠加，最后表现在鼓面的倾斜角度差异，最终得到表1.

表1 鼓面斜角数据

分析求解出来的表格数据可以看出，提前发力或增大发力力度会使得鼓面倾角增大.对称分布的8名队员中，同一侧的作用效果相互叠加，鼓面倾角增大；异侧的作用效果相互抵消，鼓面倾角减小.

2.4.4 模型建立及问题的求解

在游戏开始的那一刻由于八名队员之间的用力大小和时机不同，鼓面会发生一定程度上的倾斜.这样一来撞击的时间和位置都会发生变化，为了使问题一中的策略依然成立，我们将策略做一些改动.

由于鼓面在发生撞击之前就已经发生倾斜，需要时间调整.由于球的下落时间与球的最高高度成正比，即球在做初速度为0，加速度为g的恒加速运动.

由牛顿第二定律可得：

其中：x为数值位移，t为运动时间.

由此我们的策略调整为适当升高球弹起的高度，预留时间去做调整，使得当球每次落在水平面时，始终可以保持鼓面以水平的姿态去撞击，依然使高度尽可能的小，来保证在单位时间内击球的次数尽可能的多这一大前提不变.

2.4.5 鼓面调整时间的计算

由问题2倾角计算模型可知数值位移与水平位移之比计算出在一段时间之后鼓的倾斜角度，由公式(3)、(4)、(5)可得：

根据前文所述，可知反向加速度矢量和满足如下关系式：

其中：F-Σy为反向竖直力的矢量和，大小等于FΣy(下同)，F-∑x为反向水平力的矢量和，a-x为反向水平加速度、a-y为反向竖直加速度,并且已知该点的水平速度和位移速度，所以根据牛顿定律，整理可得，时间t满足如下关系式：

vx=a-x·t特

vy=a-y·t特

其中:v-y、v-x分别为反向竖直速度和反向水平速度，大小不变，方向均与原方向相反，Φ为第二问中求出的鼓面的倾斜角度.

所以我们将问题抽象为质点在水平方向和竖直方向的加速度方向与速度方向反向(图10所示)的减速运动并使位移求和最终为零.

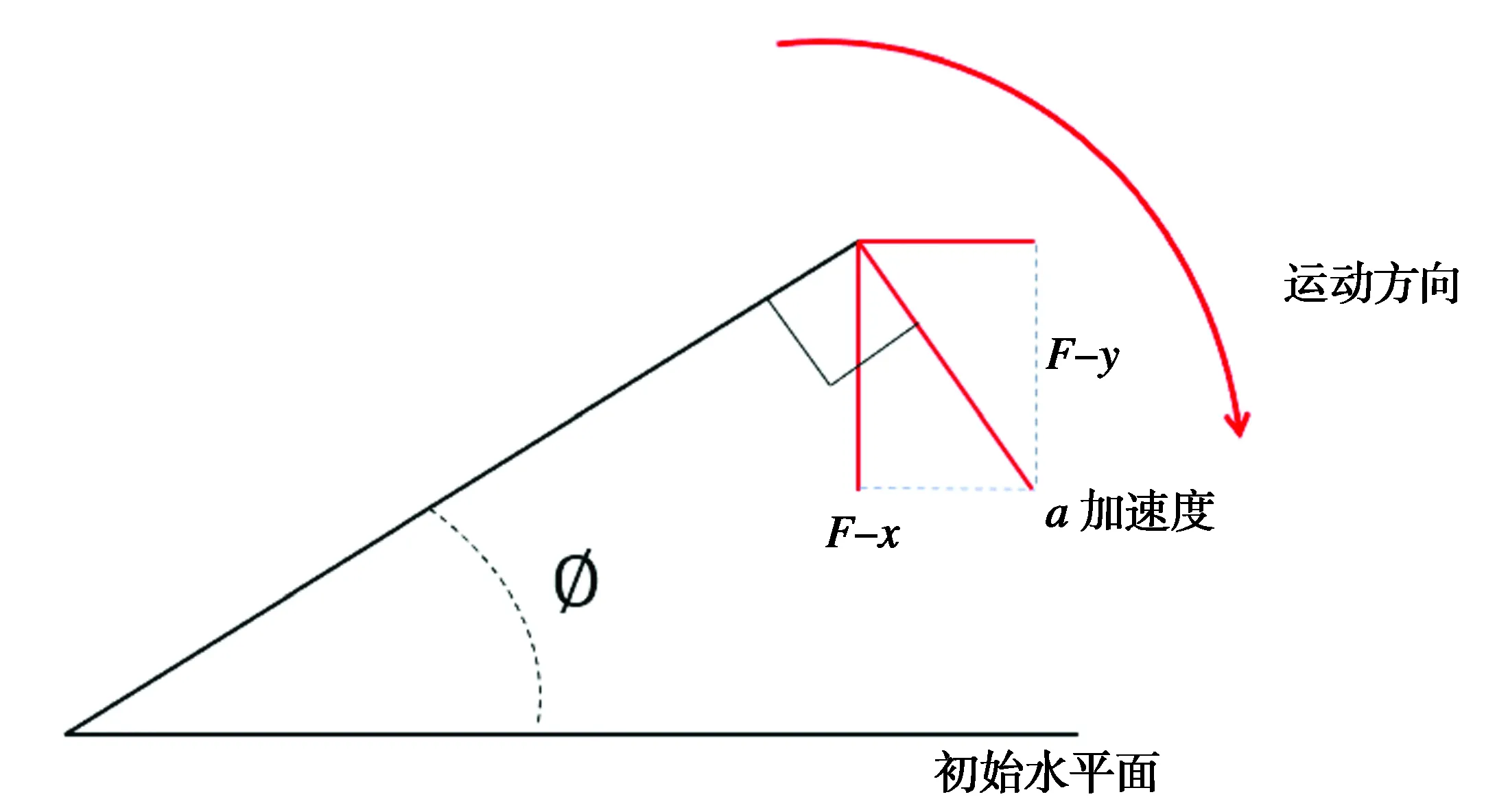
图10 由倾斜恢复至水平受力示意图

2.4.6 数值向上合力大小的计算

合力计算依据第二问情况1，作为算例.已知回复时间可算出鼓面恢复水平时间，利用此时间，反推球与鼓撞击前的速度大小.依据速度大小，亦可反推竖直合力，故需要给出计算结果，如图11所示.

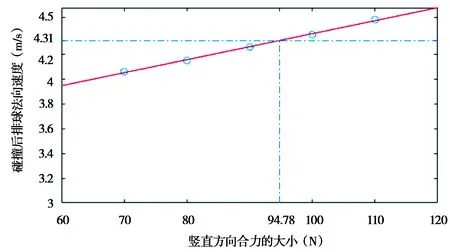
图11 鼓面倾斜下撞击力示意图

2.5 问题三模型建立及问题的求解

2.5.1 模型的建立——碰撞速度的矩阵模型

考虑鼓面与排球的碰撞，对碰撞前与碰撞后的速度关系使用矩阵来简明表达，分析碰撞之前与碰撞之后的能量组成和其关系，求出能量损失和传递率的表达式，以便解决鼓面与排球的碰撞问题.

以下为碰撞速度的矩阵模型的表示方法：

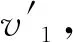
根据动量守恒定理，有：

(6)

因为有恢复系数e则有：

(7)

即：

u′=-eu

(8)

综上可得：

(9)

(10)

使用矩阵来表示碰撞前后的速度关系为：

(11)

可得鼓与排球之间碰撞前与碰撞后的关系：

(12)

(13)

使用矩阵表示为：

(14)

由此即建立了碰撞速度的矩阵模型.

2.5.2 模型的求解——能量分析的方式

经过分析，碰撞前后，鼓与排球的动能分别为：

(15)

(16)

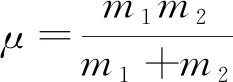
该碰撞系统的能量损失为碰撞前后的有效动能之差：

(17)

(18)

由碰撞前后的矩阵表示可得：

(19)

(20)

结合上述公式，可得Ed为：

(21)

比较ΔEk可知，Ed=ΔEk，碰撞前后系统的有效动能相等.

鼓传递给排球的动能E2g与鼓的动能之比为能量传递率η，其为：

(22)

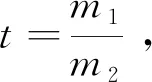
(23)

恢复系数e的值介于0与1之间，能量传递率η与鼓与排球的质量比t和恢复系数e有关，为了使η最大，作如下讨论：

(1)若t恒定，则e=1时，发生完全弹性碰撞，η最大，e=0时，发生完全非弹性碰撞，η最大.

结合上述公式，使用Matlab编程得到图12，由此可得：10名队员在调整相对于竖直方向倾斜角度为1度的排球时，每位队员应该发力的时机，由此可知位于2、4、8号位置队员需要提前发力，其余位置的队员需要晚一拍才发力，这种策略把排球恢复为相对于竖直方向倾斜角度为0度.

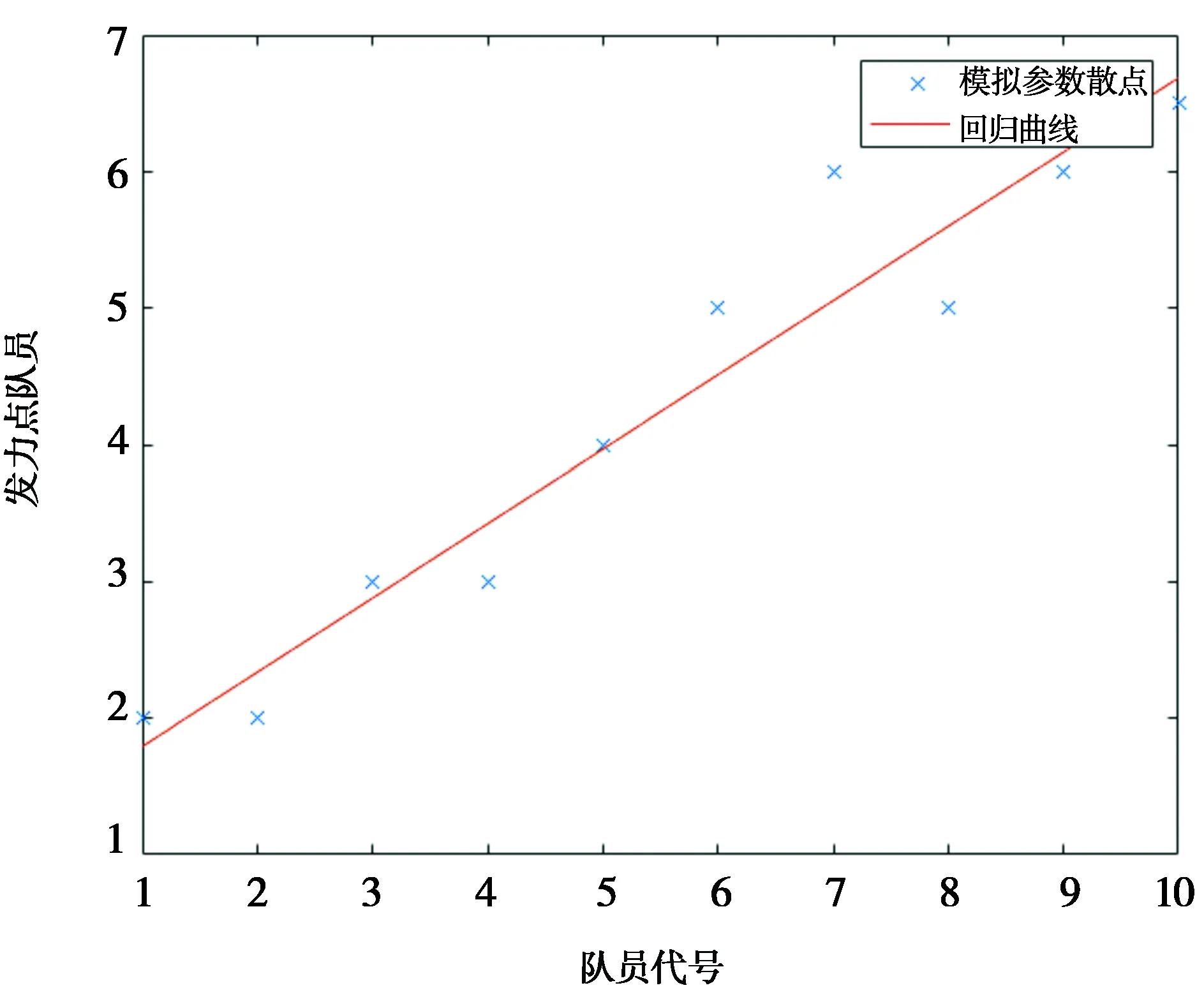
图12 调整排球至竖直弹跳每个队员应该发力的时间点示意图

3 结语

(1)本文运用了Matlab工具准确地对数据进行了处理，并利用Simulink系统来对数据进行仿真和计算，同时进行数据拟合.能够准确得到理想的曲线以及图像，比如鼓膜与排球发生碰撞之后，建立竖直方向合力大小与碰撞后排球法量速度的线性关系图；

(2)建立模型的时候充分考虑了排球和鼓面的材料的泊松比，弹性模量以及曲率半径，求得的数据更为接近实际情况;

(3)采用了经典力学接触模型，这种模型主要使用恢复系数来描述接触碰撞的过程，是一种对碰撞过程的简化处理方法;

(4)动态接触模型可将接触现象作为连续的动力学过程进行处理，能比较简化地求解碰撞过程中各个物理量的时间变化过程.

模型的缺点:

(1)由于忽略空气因素对球的影响，实际上排球弹起在空中时都是带一定程度的自旋的，这种球体自发性的旋转会与空气产生一定的摩擦，这种摩擦会损耗球体运动的总能量;

(2)建立模型的时候考虑鼓膜表面的振动频率和排球形变的约束条件时不够细致，在实际情况中在排球与鼓膜碰撞的那一刻是会互相作用力的，这个力包括鼓膜表层的振动和排球的形变，这个约束条件可以更进一步地去完善模型;

(3)在计算模型的时候由于数据量较少，导致仿真和计算时会产生偏差，尤其是求解的时候，倘若数据量更多一些的话最终求出来的值和角度会更加的仿真.