关于星匹配数的图能量下界
2020-09-27 08:41王蒙蒙何常香
上海理工大学学报 2020年4期
王蒙蒙, 何常香
(上海理工大学 理学院,上海 200093)
1 问题的提出



2 关于 K1,s −匹配数的图能量下界
设S⊆V(G),S是S在V(G)中的补集,以[S,S]表示一端在S中、另一端在S中的所有边构成的集合。文献[8]中得到了关于图能量的2 个结论,为引理1 和引理2。
引 理1[8]若E0是简单图G的割集,则ε(G−E0)≤ε(G)。
引理2[8]设H是图G的诱导子图,E0=[H,H],若E0非空,并且E0中的所有边都恰与H中的某一个点相关联,则ε(G−E0)<ε(G)。
引理3设G1和G2是G的2 个互补诱导子图,若[v(G1),v(G2)]是一个星图,且G1有完美K1,s−匹配,则µs(G)=µs(G1)+µs(G2)。

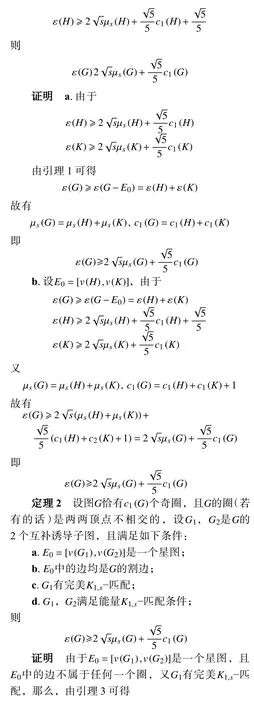


猜你喜欢
军事文摘(2022年12期)2022-07-13
数学大世界(2021年10期)2021-06-05
小型微型计算机系统(2021年10期)2021-02-28
计算机与数字工程(2019年10期)2019-11-12
综艺报(2019年15期)2019-08-16
现代装饰(2019年7期)2019-07-25
计算机与数字工程(2019年3期)2019-03-26
现代计算机(2019年2期)2019-03-02
兵工学报(2018年7期)2018-08-07
考试周刊(2017年37期)2017-12-27

