方程的两个根的和差积商的上下界

华南农业大学数学与信息学院 黄一德 田秀蓉

一、主要结果

我们把本文的主要结果写成一个定理。

（一）定理

（二）不等式（1）的证明

证明不等式（1），需要用到下面几条事实。

当0＜t＜1时，

e（1-t）＜e1-t，

2-t＜e1-t。

这些不等式可以直接证明，也可以参考文献 [2] 的5.3节不等式1，18，40，41。

四次多项式

p1（t）=（e-2）+（3e-2）t-3et2+et3-2et4

有两个实数根：

r'1=-0.1023，r1=0.7658

和一对共轭复根：

-0.0818-1.2962i，-0.0818+1.2962i。

当r'1＜t＜r1时，p1（t）＞0。

六次多项式

p2（t）=3e-8+（6e-8）t-11et2+8et3-7et4+2et5-et6

有两个实数根：

r'2=-0.0175，r2=0.3591

和两对共轭复根：

0.7229-1.3983i，0.7229+1.3983i；

0.1063-1.9087i，0.1063+1.9087i。

当r'2＜t＜r2时，p2（t）＞0。

三次多项式

p3（t）=-1+4t-4t2+2t3

有一个实数根：

r3=0.3522

和一对共轭复根：

0.8239+0.8607i，0.8239-0.8607i。

当t＞r3时，p3（t）＞0。

五次多项式

p4（t）=-4+19t-21t2+15t3-6t4+t5

有一个实数根：

r4=0.2832

和两对共轭复根：

0.5296-1.4198i，0.5296+1.4198i；

2.3289-0.8534i，2.3289+0.8534i。

当t＞r4时，p4（t）＞0。

我们不需要知道多项式p1（t），p2（t），p3（t），p4（t）的根的准确值，只需要知道r'1＜r'2＜0＜r4＜r3＜r2＜r1就够了。

令x1=et，0＜t＜1，那么a=e-tt，上条不等式可以改写为：

下面证明当0＜t＜1时，F'（t）＜0，即证明F1（t）＞0。

情形1：0＜t＜r2，

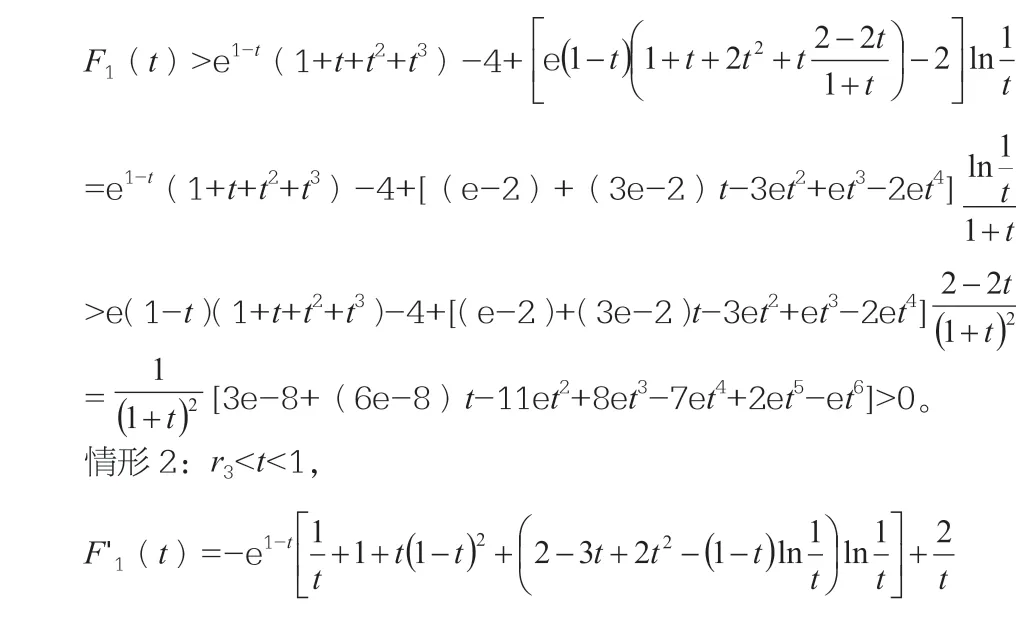
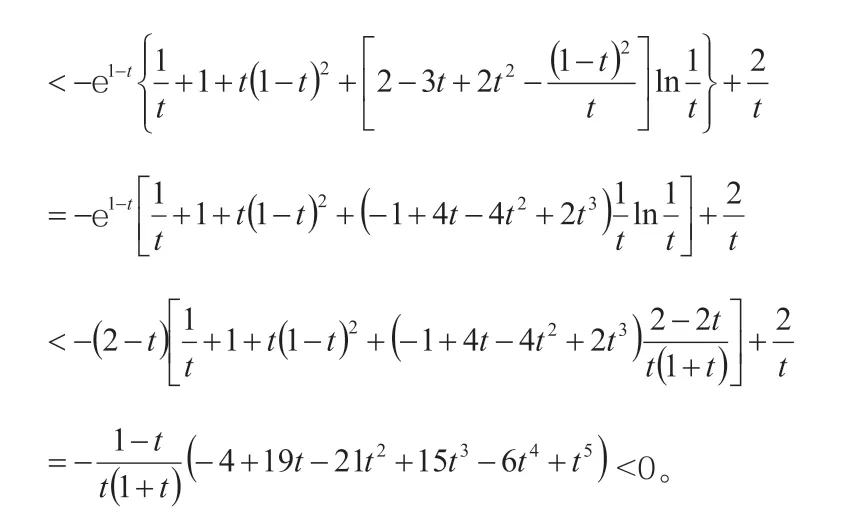
因此，在[r3，1]上F1（t）是减函数，从而当r3≤t＜1时，F1（t）＞F1（1）=0。

上面证明了当0＜t＜1时，F'（t）＜0，所以在区间（0，1）上，F（t）是减函数，从而当0＜t＜1时，F（t）＞F（1）=0。

所以在区间（0，1）上，f（t）是减函数，从而当0＜t＜1时，f（t）＞f（1）=0。

（四）不等式（3）的证明

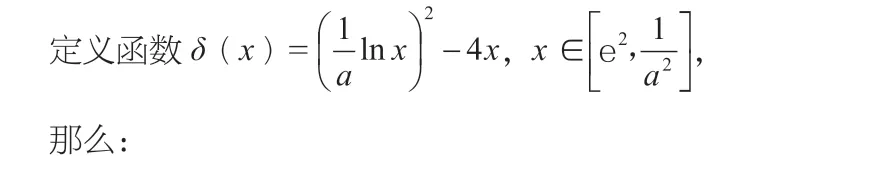
把δ作用于不等式（1）的不等号两边，再开平方，即得不等式（3）。

（五）不等式（4）的证明

因为函数θ（x）=eax，x∈（-∞，+∞）是增函数，所以把θ作用于不等式（3）的不等号两边，即得不等式（4）。

二、对主要结果的简略补充

（1）x2-x1的上下界还有

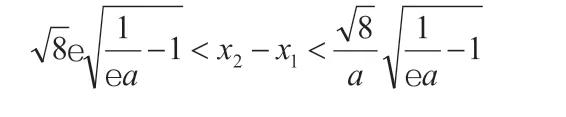
但不等式（3）的最弱的上下界都分别比这个上下界强。

（2）x1x2和x1+x2的大小有如下关系：

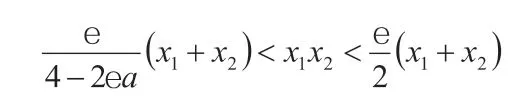
利用这个不等式，可以从x1+x2的上下界得到x1x2的上下界，或从x1x2的上下界得到x1+x2的上下界。但经验证，这种方法对定理的结果几乎没有改进作用，因此本文不详细讨论这个不等式。唯一略有改进的地方是，从不等式（2）的下界可得x1x2的一个新下界：

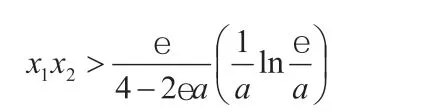
仅当a＜0.0747486400610507时，

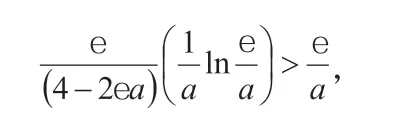
即仅当此时，这个新下界比不等式（1）的下界好。