异构属性网络中统计显著密集子图发现算法研究

李 源，范晓林，孙 晶，赵宇海

1(北方工业大学 信息学院，北京 100144) 2(东北大学 计算机科学与工程学院，沈阳 110819)

1 引 言

图模型的提出使现实世界万物得以被描述和分析，这使得图模型可以被应用到许多不同领域，例如社交网络，生物网络以及协作网络等.给定一个图G=(V，E)，其V中的顶点代表感兴趣的实体，E中的边代表实体之间的关系.则本文研究的密集子图(Densest Subgraph，DS)是图G中最稠密或具有最高密度的子图[1].而密集子图发现可以解决现实生活中的许多问题，比如它可以被用于事件检测，生物分析以及社区发现等方面.具体地，在事件检测方面，发现的密集子图是社交网络中的“稠密部分”，可代表一个事件[2]；在生物分析方面，密集子图可以帮助生物学的研究人员鉴定基因组DNA[3]和基因注释图[4]中的调控基序；在社区发现方面，密集子图可以在社交媒体中找到具有相同兴趣的社区[5]，可根据社区的特性实现产品的精准推荐和营销.因此密集子图发现这一关键问题值得被深入研究.

目前为止，密集子图发现已经在简单静态图和特定动态图中被广泛研究.1)对于简单静态图中的密集子图发现主要有基于边密度、h-团密度和模式密度的研究[6]，其主要是先定义团[7]或模式，再从图中检测其最高密度的子图；还有一种是最优类团[8]，它提取了比基于边密度更密集、直径更小的子图；当然，还有其它的密集子图发现方法，比如k-truss[9]，k-(r，s)核[10]，k-plexes[11]等.2)特定动态图中的密集子图发现方法有:McGregor等人[12]提出了在动态图数据模型上逼近密集子图的方法，其增加了对动态图的挖掘分析；Wang等人[13]提出了基于频繁结构的动态图中密集子图挖掘的方法；闫靓[14]等人提出了基于滑动窗口模型的top-k密集子图发现的方法.这使得密集子图发现能够应用到更多复杂的场景中，但上述方法检测到的密集子图并非全都显著有效.

以上图模型仍是对同构信息网络的分析，每个顶点和边没有特定的类型信息.而随着图模型以及各项技术的发展，近些年出现的异构信息网络(Heterogeneous Information Network，HIN)[15]和属性图[16]让密集子图发现有了更进一步的研究，HIN是包括不同类型的实体和关系；属性图是每种类型的实体和关系都有自己的属性信息.Fang等人[16]就提出了在属性图中进行社区搜索的算法.接着，Shin等人[17]提出了在异构信息网络中发现高密子图的算法.另外，Chen等人[18]最先提出了一种新颖的非参数扫描统计(Non-Parametric Scan Statistics，NPSS)的方法，它无需假设任何的先验分布，就可以快速准确地检测出新兴的统计显著连通子图；Nguyen等人[19]将非参数扫描统计方法运用到了社交媒体的流数据中，这让检测到的子图具有统计显著性.

以上这些方法的问题是:1)HIN仅分析了特定类型的实体及关系，没有将实体及关系的属性考虑在内；属性图虽考虑了实体及关系的属性，但是其属性是没有时序关系的，不能从时间维度来纵向分析，这使得图模型的描述不够详细，其上发现的密集子图不够准确；2)经过实验研究测试，使用上述提到的密集子图发现方法，很难在实际应用场景中发现最显著有效的密集子图；3)在基于h-团密度的密集子图发现方法和已发表的通过密集子图检测统计显著事件的文献[20]中，发现的密集子图仅是包含在(kmax，Ψ)-核中.当图中包含有较多Steiner连通度[21]为1的边时，所检测出的密集子图就偏大，不够紧凑.

针对以上问题，本文提出了以下解决方案:1)为了详细地描述图模型并使密集子图发现算法能适用于更多规模和复杂的场景.本文提出一种异构属性网络(Heterogeneous Attribute Network，HAN)的新模型，HAN是以图结构的形式详细刻画和建模某一连续时间内现实世界万物及万物之间的关系.HAN包括类型、实体、关系和带有时序关系的属性信息，其中类型包括实体类型和关系类型，每个实体和关系都有自己所属的特定类型，每个实体和关系又都有带有时序关系的属性信息，因此所提出的新模型更详细地描述了现实世界万物；2)为了使发现的密集子图具有统计显著性，本文则提出先通过收集一段时间粒度(比如:时、天、周)的连续时间的数据，在构建HAN的基础上，然后计算每个顶点的统计值[18]来处理HAN的动态性和异构性，再用非参数扫描统计的方法测量子图的显著有效性；3)在基于h-团密度的密集子图发现算法和通过密集子图检测统计显著事件算法中加入Steiner连通度的度量，使发现的密集子图更加紧凑.

综上，本文提出在异构属性网络中通过非参数扫描统计和基于(k，Ψ)-核的方法对高Steiner连通度的统计显著密集子图进行检测.具体地，首先提出新模型异构属性网络，其包括类型、实体、关系和带有时序关系的属性信息；其次，通过比较每个顶点的历史属性信息和当前属性信息，或同类型中顶点属性信息的对比计算每个顶点的统计值，从而形成统计权重网络(Statistical Weighted Network，SWN)；然后，运用非参数扫描统计的方法测量SWN中连通子图的统计显著性；最后，由于在HAN中发现高Steiner连通度的统计显著密集子图是NP-难的，于是提出了基于(k，Ψ)-核的局部扩展的近似统计显著密集子图发现算法，其内部的顶点都至少包含在k个h-团中，内部的边Steiner连通度都至少为2.

本文的主要贡献如下:

1)异构属性网络.提出了一种新颖的异构属性网络模型，其详细地描述和建模了某一连续时间内的现实世界万物，解决了以往图模型的限制.

2)统计权重网络.通过比较HAN中顶点的历史属性信息和当前属性信息，或同类型顶点属性信息对比，计算出顶点的统计值，形成统计权重网络.

3)近似统计显著密集子图发现算法.由于此问题是NP-难的，于是本文在HAN中提出有效地局部扩展的近似统计显著密集子图发现算法.

本文第2节对现有的密集子图发现问题和图模型的相关工作进行介绍；第3节给出本文所用的相关概念以及本文所解决的问题定义；第4节详细阐述HAN中顶点统计值的计算，从而形成统计权重网络；在此基础上，第5节详细介绍测量统计显著性的非参数扫描统计方法和近似统计显著密集子图发现算法；第6节通过在真实HAN数据集上的实验分析算法的有效性和高效性；第7节则总结全文.

2 相关工作

密集子图发现问题已经被广泛研究[1]，下面将对现有的密集子图发现工作进行总结.本节首先介绍基于简单静态图、特定动态图中密集子图发现的方法.

1)基于简单静态图的密集子图发现方法.简单静态图类似于同构信息网络，其上的密集子图发现方法主要有基于边密度，h-团密度和模式密度的方法.基于边密度的密集子图发现方法[6]如下:给定一个无向图G=(V，E)，n=|V|，m=|E|，则边密度为m/n.其上的密集子图发现是找到图G中所有可能子图中边密度最大的；它的另一版本是最优类团[8]，提取了比基于边密度更密集、直径更小的子图.基于h-团密度的密集子图发现方法同边密度的方法，是找到h-团密度最大的子图.Epasto等人[22]提出了在演化图上的基于边密度的密集子图发现方法.由于在大图上发现精确的密集子图效果不佳，Charikar[23]和Bahmani[24]等人分别提出了求解密集子图的贪婪近似算法.当然，简单静态图上还有其它的密集子图发现方法，比如k-truss[9]，k-(r，s)核[10]，k-plexes[11]等.

2)基于特定动态图中的密集子图发现方法.McGregor等人[12]提出了在动态图数据流计算模型中发现密集子图的方法，其动态图是通过一系列边的插入和删除来处理的.另外，Wang等人[13]提出了基于频繁结构的动态图中密集子图发现算法，其动态图是通过顶点和边的插入和删除来处理的.闫靓[14]等人提出了一种基于滑动窗口模型的top-k最密集子图发现的动态算法，有效地解决了图的动态更新.

近些年来，由于图模型的应用场景越来越复杂化，异构信息网络[15]和属性图[16]逐渐进入研究者们的视野，Fang等人[16]提出了在属性图进行社区搜索的方法，其主要是搜索满足关键词内聚和结构内聚的子图.Shin等人[17]提出了在异构信息网络中发现高密子图的算法，其主要思想是定义一个衡量顶点和边密集度的指标，然后启发式地不断优化这个值.Shi[25]等人提出了在异构信息网络上通过结合排序和聚类来发现其稠密部分.另外，本文的研究内容还增加了连通子图统计显著性的分析.Chen[18]等人提出了在异构社交媒体中统计显著连通子图发现的方法，其发现的子图不仅是连通的，而且是最显著的.Nguyen等人[19]将非参数扫描统计方法运用到了社交媒体的流数据中，通过异常检测尽早地识别特殊事件，尽早地做出对应措施.因此将此方法应用到本文的研究中将更有意义.

3 基本概念及问题定义

本节主要介绍一些基本概念及其符号表达，阐述异构属性网络的定义及密集子图的相关定义，并对本文解决的主要问题给出具体定义.

3.1 基本概念

本文用C={C1，…，Cn}表示实体类型集，则V={V1∪…∪Vn}为实体集，这里的Ci代表实体Vi的类型；同样，D⊆C×C={D1，…，Dm}表示关系类型集，则E⊆V×V={E1∪…∪Em}为关系集，这里Ei的关系类型为Di.然后，HAN的定义如下:

定义1.(HAN).一个HAN模型是一个有向图G={Q，V，E，f}，由类型、实体、关系和属性信息组成.这里的Q=C∪D={Q1，…，Qn+m}表示实体和关系总类型集合，实体和关系的属性信息f={f1，…，fn+m}是一组映射函数:fi:Qi→Rqi，其表示Qi类型t时刻的元素xt的qi维特征向量fi(xt).以微博为例，图1(a)详细阐述了HAN模型的结构.

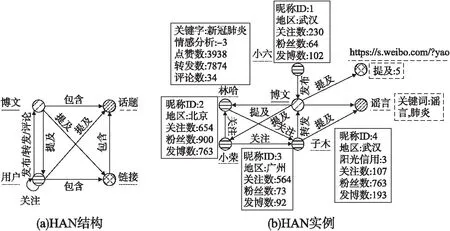
图1 HAN结构和实例

此HAN选择的实体类型有用户{昵称ID，地区，阳光信用，关注数，粉丝数，发博数}、博文{关键词，情感分析，地区，点赞数，转发数，评论数}、话题{关键词}、链接{提及数}；同时关系类型有用户-用户{关注类型}、用户-博文(发布，转发，评论，提及){时间}、用户-话题{时间}、用户-链接{时间}、博文-链接{提及数}、博文-话题{提及数}、链接-话题{时间}.每个实体和关系还有它们对应的属性及属性值.另外，本文将属性信息分为两类，分别为动态属性和静态属性.动态属性表示随时间变化的属性，静态属性表示不随时间变化.特别地，每个实体和关系后大括号中的内容是它们所对应的属性信息.图1(b)是关于武汉出现不明原因新冠肺炎这一HAN实例.

定义2.(h-团，Ψ).在无向图G=(V，E)中，一个h-团(h≥2)是一个子图S=(Vs，Es)，这里的Vs有h个顶点，并且Vs∈V，∀u，v∈Vs，(u，v)∈E.

定义3.(h-团度).在无向图G=(V，E)中，图G中的顶点v关于h-团的团度，即degG(v，Ψ)是包含v的h-团的个数.

定义4.(h-团密度).在无向图G=(V，E)中，图G中关于h-团Ψ(VΨ，EΨ)的h-团密度，即ρ(G，Ψ)=η(G，Ψ)/|V|，这里的η(G，Ψ)是图G中Ψ的个数.

定义5.((k，Ψ)-核).一个(k，Ψ)-核，即Hk是在图G=(V，E)满足∀v∈Hk，degHk(v，Ψ)≥k的最大的子图，这里的k(k≥0)是个整数，Ψ是h-团.

Hk有k阶，顶点v∈V的团核数，即coreG(v，Ψ)是包含v的(k，Ψ)-核的最高阶.kmax是最大团核数.

例如，图2是图1(b)的简化版，便于分析(k，Ψ)-核.让Ψ为3-团，图2中最左下顶点的团度为3，图2的3-团密度为5/7.另外，图2中每个矩形上大括号中的数字代表了矩形包围的(k，Ψ)-核中的k.因为图2最左下的4个顶点组成的子图是4-团，它中的每个顶点都有3个3-团参与，故它为(3，Ψ)-核.

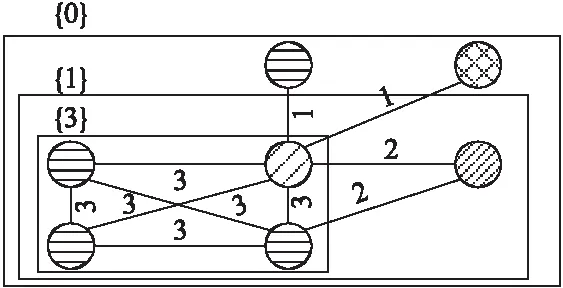
图2 HAN实例的简化版

定义6.(连通度).在无向图G=(V，E)中，V中两个不同顶点u和v之间的边连通度，即λ(u，v)是其移除将u和v断开连接的最小的边数.图G的连通度λ(G)=minu，v∈Vλ(u，v)是图G中任意两个不同顶点的最小连通度.

定义7.(Steiner连通度).在无向图G=(V，E)中，V中两个不同顶点u和v的Steiner连通度，即sc(u，v)是(u，v)的任意最大连通Steiner子图(Steiner Maximum-Connected Subgraph，SMCS)的连通度.

SMCS是图G中的一个子图Suv，其满足λ(Suv)是最大的.例如，图2的连通度是1，边上的值是对应顶点间的边Steiner连通度.

3.2 问题定义

基于以上的定义，本文给出了在异构属性网络中局部扩展的近似统计显著密集子图的问题定义.

问题.给定一个HAN为G=(Q，V，E，f)和h-团Ψ(VΨ，EΨ)(h≥2)，首先得到统计权重网络Gw，然后从Gw中识别具有最高h-团密度ρ(Gw，Ψ)和较高Steiner连通度的统计显著密集子图S.

接下来的章节，首先阐述HAN中顶点统计值的计算，然后阐述近似统计显著密集子图发现算法.

4 HAN中顶点的统计值

本节通过计算每个实体的统计值来解决HAN中不同实体类型的异构性和HAN的动态性.首先，不需要任何的假设，为每个属性建立基线分布来表示它的正常行为；然后，再为每个实体估计一个统计值，该统计值表示实体的显著程度，该值越小就越显著.

为了估计每个实体属性的基线分布，需要收集一个分布估计训练样本数据.首先定义一个时间粒度(比如:时、天、周)，然后收集HAN连续相同时间粒度的一段历史观测数据.本文将历史观测数据分为两类:充足观测数据和非充足观测数据.以下是这两种历史观测数据统计值计算的详细介绍.

4.1 充足观测数据统计值的计算

充足观测数据集由XT={x1，…，xT}表示，其中xi为第i时间粒度实体x的数据.首先，通过比较属性的历史观测值与当前观测值计算每个实体中所有属性的统计值；然后，通过交叉检验来计算这个实体的统计值.在原假设没有特殊情况发生时，这个统计值解释了从历史观测值中随机选择的样本大于等于当前观测值的概率.

实体属性的统计值:实体x∈Qi类型的属性j∈[1，qi]的统计值定义为:

(1)

其中fi，j(xT)是指当前时间T下实体x所属Qi类型第j维的属性.实体x属性的统计值p(fi，j(xT))表示历史观测值fi，j(xt)大于等于当前观测值fi，j(xT)的概率.

实体的统计值:实体x∈Qi类型的统计值定义为:

(2)

其中pmin(xt)=minj=1,…,qip(fi，j(xt))代表在当前时间实体x所有属性统计值的最小值.实体x的统计值p(xT)表示历史属性的最小值pmin(xt)小于等于当前属性的最小值pmin(xT)的概率.

不将实体属性的统计值p(fi，j(xT))和所有属性统计值的最小值pmin(xT)作为最终的统计值，是因为上述两种统计值在进行非参数扫描统计时会偏向于具有更多属性的实体[18].而用属性之间不同时刻下统计值的最小值来交叉验证得到当前时刻最终的统计值，这样的统计值p(xT)在原假设下是服从[0，1]上的均匀分布的.

4.2 非充足观测数据统计值的计算

对于非充足观测数据，本文比较同类型间实体的差异.同类型实体的观测数据表示为XQi={x1，…，x|Qi|}.在原假设没有特殊情况发生时，这个统计值反映了同类型中随机选择的不同于当前考虑的实体的观测值大于等于当前考虑实体观测值的概率.

实体属性的统计值:实体x∈Qi类型的属性j∈[1，qi]的统计值定义为:

(3)

其中fi，j(x)是指同类型中实体x∈Qi类型的第j维的属性.实体x属性的统计值p(fi，j(x))表示同属Qi类型的其它实体的观测值大于等于当前所考虑实体x观测值的概率.

实体的统计值:实体x∈Qi类型的统计值定义为:

(4)

其中pmin(xq)=minj=1，…，qip(fi，j(xq))代表了同类型实体所有属性的最小值.实体x的统计值p(x)表示同类型实体属性的最小值pmin(xq)小于等于当前实体属性的最小值pmin(x)的概率.同样地，以这种方式计算的统计值也服从[0，1]上的均匀分布.最终得到了HAN中每个实体的统计值，形成统计权重网络Gw={C，V，E，p}.

5 近似统计显著密集子图发现算法

本节提出在统计权重网络中局部扩展的近似统计显著密集子图发现算法.接下来，本节首先详细阐述如何测量子图的统计显著性.

5.1 非参数扫描统计

为了测量子图的统计显著性，本文在统计权重网络中使用非参数扫描统计[26]的方法.其方法定义如公式(5)所示:

(5)

其中S表示一个连通子图，A(S)指的是S的统计显著分数.αmax(αmax<1)是最大的统计显著水平，这意味着S至少有1-αmax的统计显著性.V(S)是S中所有顶点的个数，Vα(S)=∑v∈V(S)I(p(v)≤α)是S中统计值小于等于置信水平α(α>0)的顶点的个数.φ(α，Vα(S)，V(S))指的是非参数扫描统计方法，即把在水平α处有显著意义的顶点的个数Vα(S)与它的期望E[Vα(S)]作比较，又因为在原假设没有特殊情况发生时，统计值是服从[0，1]上的均匀分布的，即E[Vα(S)]=αV(S).

因此BJ统计量[27]可以直接将Vα(S)和V(S)作比较，BJ统计量的数学形式为:

(6)

这里的KL是Kullback-Liebler散度，意味着统计值小于α的观察个数占总个数比例与其期望值的差异.KL被定义为:

(7)

5.2 近似统计显著密集子图发现算法

在复杂应用场景中，仅仅发现密集子图是远远不够的，因为密集子图缺少在实际场景中的显著有效性，因此本文提出近似统计显著密集子图发现算法.

具体地，首先由第4节得到一个统计权重网络Gw={C，V，E，p}，其每个顶点的权重p表示它的统计值，统计值越小越显著.然后在统计权重网络中通过非参数扫描统计识别到统计显著密集子图.为了使子图更紧凑，增加了边Steiner连通度的考量，文献[21]则提出了计算连通图中任意一条边的Steiner连通度的方法.

由于在统计权重网络中发现统计显著的连通子图是NP-难的[19]，所以本文的问题也是NP-难的.而且在大的网络中发现精确的基于h-团密度的密集子图是不切实际的，又因为(kmax，Ψ)-核作为密集子图具有1/VΨ的近似比保证.

因此基于(k，Ψ)-核，本文提出一种高效地发现top-r不连通的统计显著密集子图近似算法.伪代码如算法1所示，它将统计权重网络Gw作为输入；每种实体类型中的种子个数为K；种子顶点的最大扩展数为Z.输出top-r的统计显著密集子图，以S表示.

算法1的主要思想是从种子顶点局部扩展到其边Steiner连通度最大的邻居顶点，然后迭代地增加满足统计值和团核数限制的顶点到当前子图R中.具体地，首先通过(k，Ψ)-核分解[6]计算Gw中每个顶点v的团核数coreGw(v，Ψ)，并根据团核数按非增顺序排列顶点(行1-2)；再计算每条边的Steiner连通度[21](行3).然后从剩余子图RD中的每种实体类型中选择一个种子顶点，并将它加入到当前子图R中(行7).其次，由算法2计算出R中有最大边Steiner连通度的邻居顶点(行11)，再迭代地在R和它的邻居顶点中扩展具有最高显著分数A(S)的子图S[19]，然后由算法3将子图S收缩至密集子图Sd，Sd中最大的团核数不小于当前子图R中的最小的团核数(行9-13).在每次迭代中，Sd被更新为R.当R不能被进一步扩展时，迭代就终止了(行14-16).通过这样的算法，最终得到的子图保证具有最大显著分数A(S)和团核数coreGw(v，Ψ).

正确性分析.算法1本质上是从种子顶点开始局部扩展并发现近似统计显著密集子图，这些子图具有最大的显著分数和团核数且边Steiner连通度至少为2.而对于每个当前子图R，它通过算法2得到当前边Steiner连通度最大的邻居顶点；通过HSS函数[19]计算得到有最大显著分数的顶点，该函数已在5.1节中证明；最后通过算法3将最大团核数不小于当前子图R中的顶点加入.而迭代停止标准(行14)确保了当前子图R是局部的近似统计显著密集子图，即剩余图中顶点没有满足是和当前子图R连通且满足边Steiner连通度、显著分数和团核数的顶点.

算法1.ASSDSD算法

输入:一个统计权重网络Gw={C，V，E，p}；

每种实体类型中种子顶点个数，K(默认为5)；

种子顶点的最大扩展数，Z(默认为log(|V|))；

输出:top-r统计显著密集子图，S；

1.计算每个顶点v的团核数，即coreGw(v，Ψ)；

2.根据团核数按非增的顺序排列Gw中的顶点；

3.计算每条边的Steiner连通度sc[21]；

4.αmax=0.05，S=φ，RD=V，R=φ；

5.Forc∈[1，…，n]do

6. Fori∈[1，…，K]do

7.R=R∪{vi}，vi是RD中类型为c的具有最大coreGw(vi，Ψ)的显著顶点；

8. Forz∈[1，…Z]do

9. 以团核数按递增顺序排列R中的顶点；

10.mincore是当前子图R最小的团核数；

11.Vn=SC(R，V，E)；//详见算法2

12. 〈S，A(S)〉=HSS(Vn，R，αmax)[19]；//A(S)是子图S的最高显著分数，里面的顶点具有最小统计值

13.Sd=DS(S，R，mincore)；//详见算法3

14. IfSdR≠φthen

15.R=Sd；

16. Else

17. Break；

18.RD=RDR，S=S∪{R}，R=φ；

19.返回top-r的S；

算法2.SC算法

输入：当前子图R，Gw中的顶点集V和边集E；

输出：R中最大Steiner连通度的邻居顶点集；

1. Forv∈Rdo

2.Vn={vn∈VR；(vn，v}∈E}；

3.scmax是v所有邻边中Steiner连通度最大值；

4. Forvn∈Vndo

5. If sc(v，vn)=scmaxthen

6.VN=VN∪{vn}；

7. 返回VN；

算法3.DS算法

输入：最显著的子图S，当前子图R；R中最小的团核数，mincore；

输出：密集子图Sd；

1.maxcore是SR中所有顶点的最小团核数；

2.Sd=R；

3.ifmaxcore≥mincorethen

4. forv∈SRdo

5. ifcoreGw(v，Ψ)=maxcorethen

6.Sd=Sd∪{v}；

7.返回Sd；

6 实验结果与分析

6.1 实验环境配置

本文用真实的微博数据集对所提出的算法进行有效性和高效性的评估.本实验所用的软硬件环境如下:Windows 7旗舰版操作系统，Intel(R)Core(TM)i5-3337U的CPU，主频1.8GHz，8G内存，1T硬盘；开发平台为JetBrains PyCharm 2019，开发语言为Python 3.

6.2 实验所用数据集

为了有效地构建HAN模型及评估所提出的算法，本文选择微博上的谣言事件进行评估.因为微博提供了官方的辟谣服务，所以本文收集了从2019年12月1日-2020年4月30日的微博谣言数据.收集数据的统计信息如表1所示.

表1 微博谣言数据集

6.3 实验评估指标

由于本文增加了密集子图统计显著性的研究，所以本文选择lead time和lag time来评估所发现子图的统计显著性.另外，还有coefficient和runtime指标，4个指标的具体概念如下:

1)lead time.这指的是密集子图还没有形成时，预测该子图到密集子图刚形成之间的天数.

2)lag time.这指的是密集子图刚形成到检测到该统计显著密集子图之间的天数.

3)coefficient.这是应用在图中精确率和召回率的结合体.由于密集子图通常表达为事件或社区等，故令coefficient=|E∩E*|/|E∪E*|，这里的E是事件或社区相关的实体集，E*是算法检测技术标记的实体集.

4)runtime.本文所提出算法和对比算法的运行时间.

接下来，首先比较4个算法的有效性和高效性，即ASSDSD算法、IncApp算法[6]、NPHGS算法[18]和HeProjI算法[25].然后，对比不同参数下算法的有效性和高效性.

6.4 微博谣言数据集中算法性能分析

密集子图的统计显著性评估需要时序关系，而IncApp算法和HeProjI算法所使用的图模型是没有时序关系的，故先评估4个算法的coefficient和runtime.

6.4.1 4个算法的有效性和高效性分析

本次实验通过随机去掉数据集中的数据来评估不同数据大小下算法的有效性和高效性.图3(a)和图3(b)显示了不同数据大小下的4个算法对比.x轴上的数字代表了目前数据大小占原始数据的百分比.可以看到不同数据大小下ASSDSD算法在coefficient上都优于其它的算法.这是因为ASSDSD算法所考虑的子图更加紧凑且具有统计显著性.而在runtime上会花费更多的时间，是因为检测子图考虑了更多的限制条件.

图3 4个算法有效性和高效性对比

由于IncApp算法和HeProjI算法所使用的图模型没有时序关系，所以本次实验仅比较了ASSDSD算法和NPHGS算法的lead time和lag time.在图3(c)和图3(d)中评估了不同数据大小下的ASSDSD算法和NPHGS算法，可以看到ASSDSD算法都优于NPHGS算法，因此检测的子图显著性更高.

6.4.2 不同参数下算法的有效性和高效性分析

由于初始参数对算法的有效性和高效性有重要影响，故以下进行不同参数下算法的有效性和高效性对比.而由于ASSDSD算法和NPHGS算法所使用的图模型近似，其参数也近似，故仅对这两个算法进行不同参数下的指标对比.共有的参数分别为:K，种子顶点的个数；αmax，最大的统计显著性水平；Ψ，h-团.下面首先是不同种子顶点数下的指标对比.

1)不同的种子顶点数(K)

本次实验设置初始参数αmax=0.05.图4展示了不同种子顶点数下ASSDSD算法和NPHGS算法的4种指标对比.首先，可以看到在平均的lead time、lag time、coefficient下，本文所提出的ASSDSD算法都优于NPHGS算法.这主要是因为ASSDSD算法综合了子图统计显著性和密集性的考虑，让检测的子图更加有效和紧凑.另外，运行时间也变快了.它的主要原因是因为所提出的算法在每次迭代中忽略了没有出现在密集子图中的顶点，让每次检测时都对顶点做了筛选.

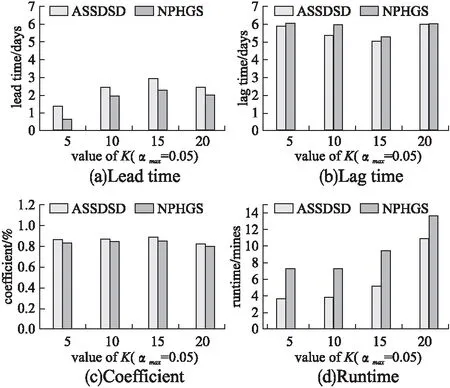
图4 不同种子顶点数下的指标对比

2)不同的最大统计显著性水平(αmax)

本次实验给ASSDSD算法和NPHGS算法设置了初始参数K=15.图5显示了ASSDSD算法和NPHGS算法的4种指标对比.通过图5可以看到对于不同的αmax，本文提出的ASSDSD算法在4种指标下均是优于NPHGS算法.这主要是因为本文综合考虑了子图的内容和结构内聚性.

图5也展示了随着αmax的增大，对lead time、lag time、coefficient这3个指标均没有很大影响，仅有稍微提高.其原因是αmax是人工设置的，并且公式(5)可以自动优化α.另外，运行时间的提高是因为αmax越大，更多的顶点需要被考虑.

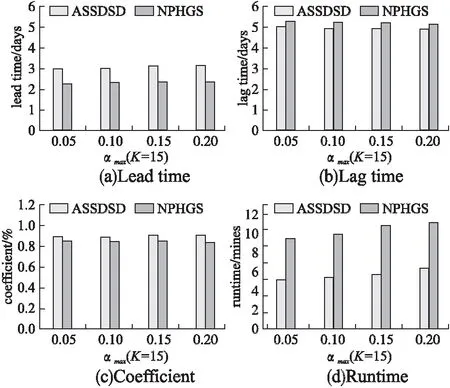
图5 不同αmax下的指标对比

3)不同的h-团

为了执行所提出的ASSDSD算法，需要选择h-团.因此，本次实验评估了在不同h-团下的ASSDSD算法的性能指标.在图6中，随着h的增大，coefficient提高的原因是密集子图通常表达为事件或社区，但是lead time、lag time和runtime是先增加后减少.这主要是因为当h设置的越大时，所检测的子图必须包含越密集的团，这需要花费更多的时间；然而当h超过一定的范围，HAN中或许没有这么密集的团，因此检测会提前终止.

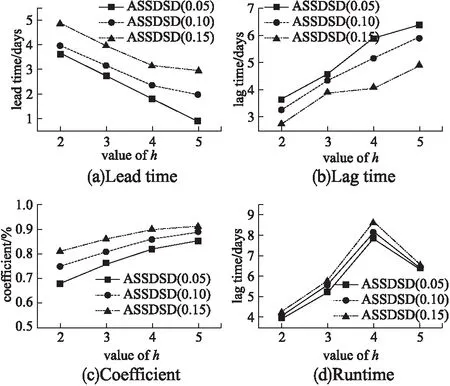
图6 不同h-团下的指标对比

7 总结与展望

密集子图发现已经被广泛研究.针对现有的简单图模型和不同图模型下发现的密集子图不够紧凑，缺乏显著有效性的问题.本文提出了异构属性网络模型；并结合图模型的内容和结构设计了基于(k，Ψ)-核的近似统计显著密集子图发现算法.最后，在大量真实数据集上的实验验证了本文提出模型和算法的有效性和高效性.对于未来的密集子图发现问题研究，由于图模型的不断发展，还需设计更通用的方法满足不断发展的需求.