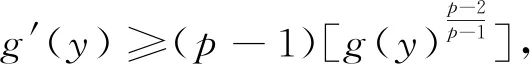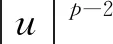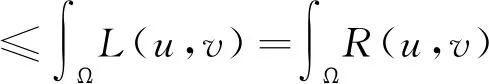关于各项异性Heisenberg群上几个不等式、定理、原理的探究

王胜军

(青海师范大学 数学与统计学院，青海 西宁 810008)

1 引言

文献[1]首先建立Heisenberg群上的Picone恒等式

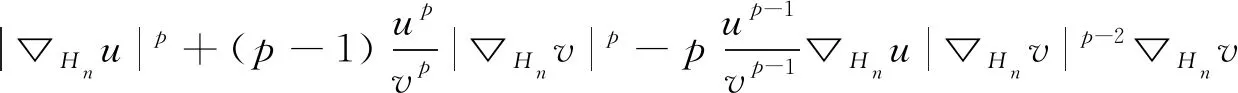
(1)

其中:u≥0，v>0，同时u，v是可微函数.接着建立了Heisenberg群上的Hardy不等式

(2)

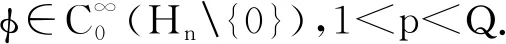
(3)

最近，文献[3]在欧式空间上，关于p-laplace算子给出了如(4)式的更加一般的Picone恒等式

(4)

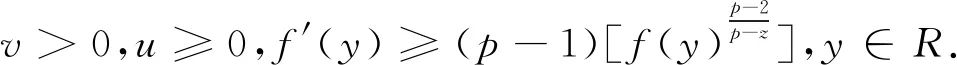
本文首先使用类似文献[3]的方法将公式(4)推广到各项异性Heisenberg群上，得到一类广义Picone型恒等式(这个结果包含了公式(1))；接着利用这个结果，使用类似于文献[4]的方法建立了各项异性Heisenberg上的广义Hardy型不等式(得到了类似公式(3)的结果)，建立了各项异性Heisenberg群上的Barta不等式、广义Liouville型定理及广义Sturmian比较型定理.

下面陈述了有关各项异性Heisenberg群的一些基本知识，更多详细的内容以及证明可参考文献[2]、文献[4]-[7]及其中的参考文献.

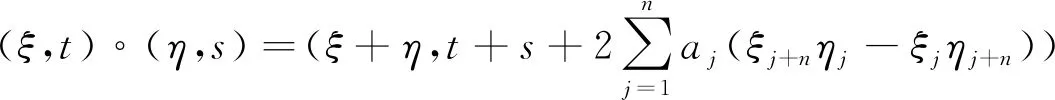
(ξ，t)=(ξ1，ξ2，…，ξ2n，t)，(η，s)=(η1，η2…，η2n，s)∈R2n+1.对于(x，y，t)∈R2n+1，x=(x1，x2，…，xn)，y=(y1，y2，…，yn)，下列向量场

(5)

构成了其李代数的基底.容易得到向量场X1，…，Xn，Y1，…，Yn满足Heisenberg交换关系

而且是左不变的.

由(5)式中的向量场X1，…，Xn，Y1，…，Yn构成H(a)上的次Laplace算子

(6)

是亚椭圆的和左不变的，相应的水平梯度和散度分别为

▽H=(X1，…，Xn，Y1，…，Yn)，

H(a)上的p次Laplace算子形为

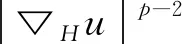
相应于(6)式中的算子△H的一族各项异性的伸缩为

δτ(x，y，t)=(τx，τy，τ2t)，τ>0，(x，y，t)∈R2n+1.

(7)

由(7)式诱导的拟距离为

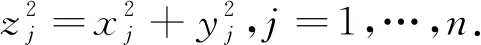
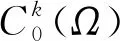
2 各项异性Heisenberg群p-退化椭圆算子的一类广义Picone恒等式

下文中，总是假设g满足下列条件，g：(0，∞)→(0，∞)是局部Lipchitz函数，且在(0，∞)上

(8)

几乎处处成立.

定理2.1(广义Picone恒等式)若10，且g满足(8)式，设

则L(u，v)=R(u，v)≥0.而且在Ω上L(u，v)=0几乎处处成立的充要条件是在Ω上u=kv几乎处处成立，其中k∈R.

证明直接计算

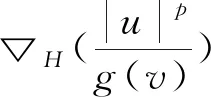
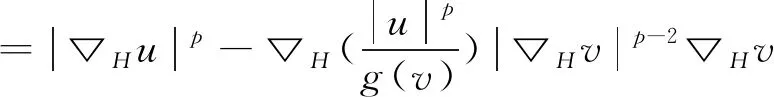
得到L(u，v)=R(u，v).应用Young不等式及(8)式，有

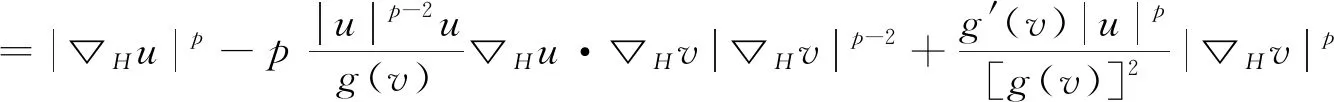
这样L(u，v)=R(u，v)≥0.

由以下三个等式同时成立，

L(u，v)=R(u，v)，

可以得到：

(9)

令

当v∈ω，由(9)得到

从而，有

(10)

当v∈ωc，设

由L(u，v)=0，得

上式中，取g(v)=vp-1，得

(11)

注2.1 在定理2.1中，当Ω=H(a)时，结论仍然成立.

注2.2 在定理2.1中，取g(v)=vp-1，u≥0，得到(1)式.

3 各项异性Heisenberg群上的广义Hardy型不等式、Barta型不等式、广义Liouville型定理及广义Sturmian比较型定理

定理3.1(广义Hardy型不等式)若v∈C1(H(a))，在Ω上v>0，并且满足

-△H，pv≥λhg(v)，

(12)

等号成立的必要条件是u=kv.

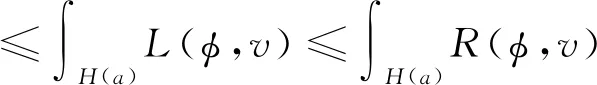
令φ→u，就得到(12).由以上推导知道

2.2 两组患者治疗前后胎儿生长指标比较 治疗前，两组患者孕20周时胎儿BPD及FL比较，差异无统计学意义(P>0.05)；治疗后，用药8周后胎儿BPD及FL显著高于治疗前(P<0.05)，且治疗组明显高于对照组(P<0.05)。见表2。

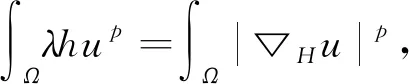
利用定理3.1，取g(v)=vp-1，容易得到类似于文献[2]中的Hardy不等式.

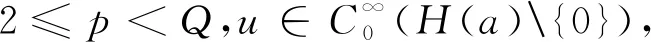
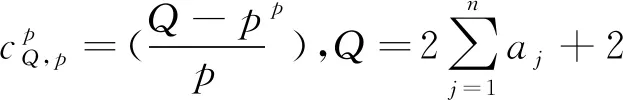
定理3.3(Barta型不定式)若v满足(12)及其条件，则下列不等式成立

等号成立时，有u=kv.

证明设

有

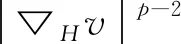
由定理3.1，得到

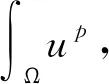
定理3.4(Liouville型定理)若c>0，g满足(8)，则不等式

-ΔH，Pv≥cg(v)

(13)

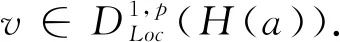
证明假定v是(13)的一个正解，φ1是相应于第一特征值λ1(Ω)的第一特征函数且λ1(Ω)

从而，得到

这是一个矛盾式，故定理3.4得证.

u=0，ξ∈∂Ω

的一个正解，则方程

-△H，pv=f2(ξ)g(v)，ξ∈Ω

v=0，ξ∈∂Ω

(14)

的任意非平凡解一定改变符号.

证明假设v>0是(14)的一个解，由广义Picone恒等式，有

这是一个矛盾式.因此假设错误.即v在Ω上改变符号.