面向高层次综合的自定义指令自动识别方法

肖成龙，林 军，王珊珊，王 宁

(辽宁工程技术大学 软件学院，辽宁 葫芦岛 125105)(*通信作者电子邮箱2437017377@qq.com)

0 引言

随着半导体技术的飞速发展以及集成电路的复杂度不断增加，在低层次的寄存器传输级(Register-Transfer Level, RTL)下手写代码、维护和仿真较困难并且极易出错。高层次综合(High Level Synthesis, HLS)是一个将高抽象层次的行为描述转换为低层次的寄存器传输级描述的自动化或半自动化编译过程，它接收基于C或C++语言的行为描述、含硬件组件详细信息的资源库以及特殊的约束条件作为输入，经过前端编译、资源分配、调度、绑定以及代码转换等过程，自动生成寄存器传输级的代码。高层次综合(HLS)可以有效解决寄存器传输级所遇到的问题，且具有设计周期短、产品质量高等优点[1-2]。

近年来，研究者致力于高层次综合的性能和能耗方面的研究。自定义功能单元(自定义指令的硬件实现)是权衡可扩展处理器灵活性和效率的重要组件[3-4]，在可扩展处理器中使用自定义指令能够有效提高运算速度、减少面积和代码量[5-6]。将自定义指令应用到高层次综合中，可以有效解决高层次综合能耗问题[7-8]。然而，现有研究多数是在高层次综合的过程中进行[7-13]，需要修改高层次综合的核心算法，实现起来相对困难。

针对以上问题，本文提出了一种面向高层次综合的自定义指令自动识别方法，主要贡献包括：

1)方法在高层次综合过程之前识别自定义指令，可适用于大部分的高层次综合工具，克服了现有研究在高层次综合过程中识别自定义指令的缺点。

2)针对子图枚举，结合搜索树设计了一种基于节点删除技术的深度优先(Depth-First based on Node Deletion technique, DFND)搜索算法，可灵活修改图大小、连通性等约束条件。

3)针对子图选择，提出了基于最少子图数目的选择(Minimum number of matches based subgraph Selection, MS)算法、基于关键路径的子图选择(Critical paths based subgraph Selection, CS)算法以及基于出现频率的模式选择(frequency of occurrence based Pattern Selection, PS)算法。在测试基准程序上进行实验并对3种算法进行比较，验证了3种算法的有效性。

1 相关研究

面向高层次综合的自定义指令自动识别方法涉及两个关键问题：子图枚举问题和子图选择问题。本章分别对这两个问题进行分析。

1.1 子图枚举问题

由于寄存器的读写端口数目有限，近期的研究专注于在I/O端口约束的条件下枚举子图。Chen等[14]证明子图枚举是具有多项式时间复杂度的问题；Bonzini等[15]提出一种多项式时间的子图枚举算法；Arnold等[16]用动态规划的方法枚举出所有子图，然而当图的规模变大，这些枚举方法效率较低。自定义指令执行过程中需要保持原子性，因而在硬件功能单元中实现的自定义指令应该满足凸性[17]，Giaquinta等[18]提出枚举出最大凸子图的算法；Wang等[19]提出枚举出所有凸子图的方法；Atasu等[20]提出一种在凸性和I/O端口约束下的二元决策树的精确算法。在此基础上，Pozzi等[21]通过添加一项基于永久输入数目的修剪标准，使算法得到进一步改进。Yu等[22-23]通过合并向上和向下的锥体型子图构建连通子图，然而，该算法可能使得同一个子图被多次枚举。Xiao等[24-25]所提出的子图枚举算法利用数据流图的拓扑特性来减少部分搜索空间，从而减少了算法的执行时间。Xiao等[26]提出了一种灵活的算法，该算法可以枚举出连通子图或所有子图。Xiao等[27]将自定义指令识别应用到高层次综合之中，提出多约束条件组合的枚举算法。

在可扩展处理器的设计中，由于处理器和自定义功能单元之间存在数据通信成本，I/O端口数目是重要的约束。然而，在高层次综合的技术背景下，I/O端口的数目不再被限制[7]。Cong等[8]提出一种子图枚举算法，该算法能够枚举出所有满足用户定义的编辑距离和频率限制的子图，但是在枚举阶段应用用户定义的编辑距离和频率限制约束使一些具有较好提升性能的子图在早期被丢弃，该算法还必须使用额外的重复检查来排除冗余子图。Balister等[28]以自顶向下的方式枚举所有连通凸子图(connected convex subgraphs, cc-subgraphs)，算法至少产生了2·cc(G)-n个递归调用来枚举所有的连通凸子图。其中：cc(G)表示枚举cc-subgraphs的数目，n是图G的节点数。在这些递归调用中，只有叶节点负责生成连通凸子图。

此前国内外的研究主要是在特定约束条件下枚举子图。然而当用户增加或删除约束条件时，算法将不再适用。本文提出一种更为有效的枚举算法(DFND算法)，DFND算法只需cc(G)次调用就可以枚举所有的连通凸子图。当约束条件发生变化时，此算法以自底而上的方式灵活地枚举出满足图大小约束的连通凸子图。

1.2 子图选择问题

枚举出的候选子图被选择的原因多数是由于其在应用代码中被频繁利用，或者与其他组件相比具有较高的性能，又或者可以显著减少面积，因此，提出良好的子图选择方法对于应用程序性能提升或面积减少至关重要。针对子图选择问题，许多研究者提出了不同的方法。

Clark等[29]提出一种精确算法，旨在用最少数目的自定义指令覆盖每个节点，该算法将子图选择问题转换为单边覆盖问题。Martin等[30]尝试通过使用约束编程来解决子图选择问题，该文献对自定义指令的选择通过两种相应的调度策略实现：时间约束调度或资源约束调度。Yu等[22-23]提出一种基于整数线性规划(Integer Linear Programming, ILP)的自定义指令选择的最优方法。

由于子图选择问题的计算复杂度较高，当应用程序对应的数据流图较大时，精确算法可能无法给出最优解。而探索式方法能够高效地解决该问题。Kastner等[31]通过沿着最频繁出现的边生成子图来选择具有高出现频率的子图；Guo等[32]提出基于冲突图的模式选择算法，此算法用最少数目的模式来覆盖图，该算法在子图之间不能有重叠的前提下，使用一个目标函数贪婪地选择子图；Bozorgzadeh等[33]提出子图选择由调度决定，使重要的子图获得更高的优先级。近年来，一些元启发式算法也用来解决子图选择问题[34-36]。Cong等[7-8]将实现的子图选择算法应用在基于自定义指令的高层次综合之中。然而，该算法所选择的自定义指令会引起延迟增加的问题。为解决时延问题，Xiao等[26-27]提出基于关键路径的数学模型，提升了高层次综合效率。本文在无重叠和无循环约束条件下提出了3种不同子图选择方法，重点研究了高层次综合在性能、面积和代码量方面的内容。

2 相关定义

数据流图(Data Flow Graph, DFG)是一种有向无环图(Directed Acyclic Graph, DAG)。图G=(V,E)，顶点集V={v1,v2,…,vn}表示基本指令，边集E={e1,e2,…,en}⊆V×V表示指令之间数据依赖关系。图G的子图S=(Vs,Es)，其中Vs⊆V，Es⊆E。

定义1 凸子图。对于G的子图S，∀u,v∈Vs，若在G中u与v之间的任何路径都只经过S中的节点，则称S是G的凸子图。

在硬件功能单元中实现的自定义指令应该满足凸性，否则不能满足自定义指令执行过程中的原子性。在图1中，子图{1,2,3}是凸子图，而子图{2,3,5}不是凸子图。

图1 数据流图示例

定义2 同构图。从图G到图S的同构是一个双射f:V(G)→V(S)，使得uv∈E(G)，记为G≅S。如果图G中的顶点u和v的连线uv属于图G边的集合E(G)，则u和v映射到图S边的集合E(S)；反之亦然，则称图G和图S同构。有向图的同构是图中的节点以及边的一一对应关系。

定义3 模式。给定两个子图a和b，如果a与b同构，则创建模式P，并且子图a和b被记录在模式P中。模式是所有同构子图的图形化表示。

给定DFGG=(V,E)和子集X，子集X⊆G，X的后继或前驱如下表示。

X的直接前驱节点集：

IPred(X)={v|u∈V,v∈X,(u,v)∈E}

X的直接后继节点集：

ISucc(X)={v|v∈X,u∈V,(v,u)∈E}

X的所有前驱节点集：

X的所有后继节点集：

问题1 子图枚举。给定一个DFG,G=(V，E),枚举满足以下约束的所有子图：

1)凸性。S是凸子图。

2)连通性。S是连通的。

3)最大规模(可根据用户需求设置)。

子图满足凸性可使程序执行过程中保持原子性。由于连通子图内部数据流可减少多路选择器的使用，因而枚举连通子图。在图1中，自定义指令{1,3}是一个连通的子图，而自定义指令{1,2}是分离子图。当枚举所有连通凸子图过于复杂时，限制子图大小很有必要。多数情况下，考虑到资源重用(面积成本)，具有高出现频率的小子图更有可能被选择。

问题2 子图/模式选择。给定一个DFG，G=(V，E)和一组枚举的子图/模式，根据不同的选择方法选择一组最佳子图集，使G中的每个节点被覆盖，满足以下约束：

1)无重叠约束。两个子图可能具有共同的节点。允许重叠有时可能会改善程序运行时间，但同时增加不必要的功耗并难以生成新代码[37]，因此，本文中不允许选择的子图之间有重叠。

2)无循环约束。如果两个子图相互提供数据，则生成一个循环。在这种情况下，两个自定义指令之间会发生死锁[6]，因此，本文不允许选择的子图之间存在循环。

3 面向高层次综合的自定义指令自动识别方法

本文所提出的面向高层次综合的自定义指令自动识别方法在不修改高层次综合的核心算法前提下，高效地识别满足用户指定的不同约束条件和设计目标的自定义指令。该方法相对灵活，改进自定义指令自动识别阶段的算法就可以提升高层次综合效率方面的问题，降低了研究问题的难度。本文的方法主要由中间表示生成、子图枚举、子图选择以及代码转换组成。方法如图2所示。图2中：RTL(Register-Transfer Level)为寄存器传输级；VHDL(Very-High-speed integrated circuit hardware Description Language)为超高速集成电路硬件描述语言。

图2 面向高层次综合的自定义指令自动识别方法

3.1 中间表示生成

本文方法的第一步是自动生成源代码的中间表示，该阶段的输入是C或C++源代码。使用开源编译器GECOS(Generic Compiler Suite)将源代码转换为控制数据流图(Control Data Flow Graph, CDFG)，控制数据流图是多个基本块之间的数据依赖关系图。程序代码对应的数据流图如图3所示。

图3 源代码的中间表示

在生成源代码的中间表示后，基于控制数据流图内的数据流图进行自定义的枚举和选择。其中，子图是自定义指令的图形化表示。

3.2 子图枚举

在枚举阶段中，如果生成冗余子图，将极大地影响子图枚举效率。目前识别子图的方法存在冗余问题，需进行重复检查过滤掉重复的子图，进而额外地增加了程序的运行时间。本文提出了一种可避免产生冗余子图的子图枚举算法——DFND算法，DFND算法通过节点删除技术使所有子图只能被识别一次，提升了枚举效率。

一般情况下，可以通过添加邻居节点到预先识别的较小子图来迭代地生成较大的子图。例如，通过将相邻节点添加到k-subgraph来形成(k+1)-subgraph(如果子图中节点的数目为k，则称为k-subgraph)。然而，大的子图在枚举过程中可能被枚举多次。如图1所示，子图{1,2,3}可以通过添加节点2到{1,3}或者添加节点1到{2,3}生成，因而子图{1,2,3}可以被枚举两次。

为了避免多次枚举，DFND算法是以深度优先的方式枚举出所有子图，并在每次迭代过程中删除已经识别过的节点。从图1的DFG构建搜索树并枚举所有连通子图的DFND算法过程如图4所示，其中，枚举子图的最大节点数设为3，R={}代表记录删除的节点，如R={1}代表记录删除节点1。算法首先枚举出包含节点1的子图(子图{1})；然后，枚举包含节点1和3的子图(子图{1,3})；紧接着枚举出包含子图{1,3}和节点2的子图(子图{1,3,2})。在枚举包含子图{1,3}和节点5的子图之前，应先删除节点2。在枚举出所有的包含节点1的子图之后，当枚举包含节点2，节点3，节点4或节点5的子图时，应先删除节点1。以这种方式可以枚举出所有满足条件的子图，并且避免了任何一个子图被枚举多次。DFND算法的伪代码如算法1所示。

图4 DFND算法过程图

算法1 子图枚举算法。

Require:G//图G

Ensure:CS//CS代表所有枚举出的子图集合

1) Procedure SubgraphEnumeration()

2)R=∅; //R是记录的被删除的节点

3) for each noden∈Gdo

4)M={n};

5)CS=CS∪M;

6) call DepthFirstEnumeration(M,R);

7)R=R∪n;

8) end for

9) Procedure DepthFirstEumeration(M,R)

10) for each neighbour nodenofMandn∉Rdo

11) if SizeCheck(M) && ConversityCheck(M,n) //进行图大小约束和凸性约束检查 then

12)M′=M∪{n};

13)CS=CS∪M′;

14) call DepthFirstEumeration(M′,R);

15)R=R∪n;

16) end if

17) end for

如算法1所示，对于枚举过程中的每个子图，都需进行图大小约束检查和凸性约束检查(第11)行)。此外，该枚举算法还可以用来枚举分离子图(将算法1中的第10)行替换为M的邻居节点和非邻居节点)。

3.3 子图选择

子图选择是在枚举所有满足约束条件的子图之后进行的。由于精确算法非常耗时且通常不能在合理的时间内得出结果，因此需要更高效的启发式方法。本文提出了3种不同的启发式选择方法。3种方法考虑的约束条件如下。

1)无重叠。子图(M)或模式(P)作为候选子图时，按照式(1)检查已经选择的子图(C)与候选子图是否有重叠部分：

M∩C=∅

(1)

2)无循环。为了确保所选的子图与当前候选子图没有形成循环，应该进行无循环检查。如果当前候选子图满足式(2)，则候选子图与其他所选子图之间不存在循环：

Succ(M)∩Pred(M)=∅

(2)

其中Succ(M)和Pred(M)代表子图M的后继节点集和前驱节点集。如果候选子图经过无重叠检查和无循环检查，则该候选子图就能被加入到子图集中。

3.3.1 基于最少子图数目的选择

所选子图的数目与代码量相关，在子图选择过程中，所选子图数目越少，经代码转换后生成新代码量越少。从能耗的角度出发，在给定的数据流图中选择最少子图数目(MS算法)可以作为子图选择的一个策略。

对于选择最少子图数目的方法，所选子图包含的节点越多，子图数目越少。同时，由于自定义指令的内部数据流不包含多路选择器，因此利用所选子图内部边数目可以粗略地估计节省多路选择器的数目。然而，贪婪地选择包含节点数多的子图，其结果使一些包含少量节点却能够较好提升性能的子图被排除。根据节点数目多的子图与枚举的所有子图重叠概率大的特点，引入重叠参数。选择较少重叠的子图限制图的大小。在最少子图数目方法下，该算法根据式(3)计算每个子图的优先级：

fi=N+E+α*1/O(Mi)

(3)

其中：N表示子图Mi的节点数，E表示子图Mi的内部边数目，O(Mi)表示Mi与其他子图重叠的次数，α表示重叠权重的参数。α小于1时，重叠对最少子图数目的选择方法影响过小，导致所选子图节点数过多。为了控制所选子图节点的数目，α的取值为2较为合适。1/O(Mi)表示选择较少重叠的子图。

如图5所示，当候选子图的最大规模为3，α的值为2时，且仅考虑连通子图的情况下,计算子图M1和M2的优先级。子图M1为{1,3,4}，子图M2为{2,4,5}，图5枚举的所有子图为{{1}，{2}，{3}，{4}，{5}，{1,3}，{1,4}，{2,4}，{4,5}，{1,3,4}，{1,4,2}，{1,4,5}，{2,4,5}}，共13个子图，有5个1-subgraph，4个2-subgraph和4个3-subgraph。子图M1与所有候选子图重叠的子图有{{1}，{3}，{4}，{1,3}，{1,4}，{2,4}，{4,5}，{1,3,4}，{1,4,2}，{1,4,5}，{2,4,5}}，O(M1)的值为11。而子图M2与所有候选子图重叠的子图有{{2}，{4}，{5}，{1,4}，{2,4}，{4,5}，{1,3,4}，{1,4,2}，{1,4,5}，{2,4,5}}，O(M2)的值为10。根据式(3)，fM2=3+2+2*1/10，fM1=3+2+2*1/11，得到fM2>fM1，由于子图M2与所有候选子图有较少的重叠，最终选择子图M2。

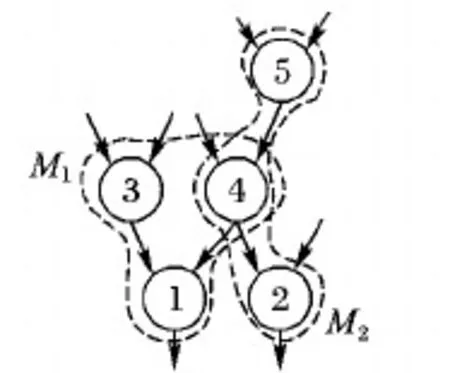
图5 基于较少重叠的子图选择

3.3.2 基于出现频率的模式选择

基于出现频率的模式选择(PS)算法从提供的一系列模式当中选择一组子集作为自定义指令。模式是一些同构子图的图形化表示。考虑到硬件资源重用，选择较少数量的模式可使得高层次综合中使用较少的面积，这样，出现频率较高的模式更可能被选择。通常，较小的模式具有较高的出现频率；然而，较小的模式可能不会带来更好的性能提升或明显的面积减少。根据式(4)，本文提出了一个可在模式大小和频率之间平衡的优先级函数：

fi=N*|M|+α*N

(4)

其中：N表示模式的大小，|M|表示模式对应的子图数目。参数α用来控制模式大小所占的权重。α>1时，模式较大，而模式出现的频率较低，不能有效地节省面积；而α<0.1时，所选模式较小，影响性能提升的效果。为了控制模式的大小，参数α取值0.3较为合适。如图6所示，当参数α的值为0.3时，模式A(PA)的大小为3，模式B(PB)的大小为1。图6按照模式A划分3个子图，按模式B划分9个子图。根据式(4)分别求PA和PB的值，fPA=3×3+0.3×3,fPB=1×9+0.3×1，fPA>fPB。模式A是更好的选择。

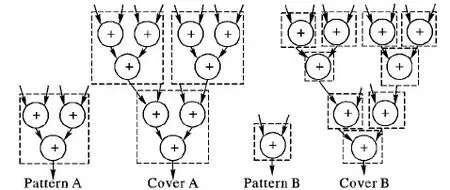
图6 选择具有更多节点的模式

3.3.3 基于关键路径的子图选择

DFG的关键路径长度与程序的运行时间有关。基于关键路径的子图选择方法(CS算法)能够在一定程度上节省时延开销。

如图7所示，假设乘法需要2个时钟周期，加法需要1个时钟周期，子图/模式的最大规模为2。当前关键路径为{4,2,1}，关键路径的长度为4个时钟周期。如果选择子图M1和M2，进一步假定每个子图需要2.7个时钟周期。显而易见，子图选择之后，关键路径的长度增加到7.4个时钟周期(乘法累加器的时间延迟要少于乘法器和加法器运算的时间延迟之和)。该选择方案最终会造成更多的时延开销。

基于关键路径的子图选择方法首先评估每个候选子图，将候选子图合并成一个节点之后，计算关键路径长度。如果关键路径长度增加，则放弃选择该子图作为候选子图。为了不增加关键路径的长度，使所选子图的节点尽量出现在关键路径上，根据式(5)按照降序排列候选子图：

fi=|M∩CP|

(5)

其中：M表示子图中的节点集合，CP表示关键路径上的节点集合。如图7所示，子图{1,2}具有比子图{1,3}更高的优先级(f{1,2}=2，f{1,3}=1)。对候选子图排序后，评估每个候选子图，不选择增加关键路径长度的子图。子图{1,2}可减少关键路径的长度，则子图{1,2}将被选择，而不选择子图{1,3}。

图7 选择子图导致关键路径长度增加的示例

由于所提出的3种方法都是启发式算法，主要区别在于给定的优先级函数，可使用通用的伪代码来描述它们(参见算法2)。

算法2 子图/模式选择算法。

Require:CS

//CS代表全部的枚举子图

fi

//功能函数

Ensure:SS

//被选择的候选子图集

SortCSin descending order according tofi;

//根据fi降序排列

whileCS≠∅ do

M=the highest prioritized candidate inCS;

if Overlapping(M,SS) and Cycle(M,SS)

//进行无重叠和无循环检查

then

if IncreaseCriticalPath(M) then

SS=SS∪M;

end if

end if

CS=CS-M;

end while

3.4 代码转换

在选择一组子图集作为候选自定义指令之后，需要确定两个选择的子图集是否可以使用相同的自定义功能单元实现。此任务可以看作是一个图同构问题，本文采用约束编程实现子图同构算法[38]。

在将功能等效的子图映射成相同的自定义指令之后，需要在表示自定义指令的代码之前增加一个特定的编译指令。自定义指令用程序语言的方法来表示。这样，高层次综合工具就会像对其他基本指令一样，对自定义指令进行调度和绑定。对于高层次综合工具CtoS(C-to-Silicon) Cadence，所有非内联函数都被默认为自定义指令，即不需要特殊编译指令。此外，自定义指令运算特定技术的时间和面积数据通过使用RTL综合工具获得。自定义指令的代码格式如图8所示。

图8 自定义指令集的代码

4 结果和分析

4.1 实验设置

本文实验的环境为3.5 GHz的i7- 47704处理器。实验使用具有丰富算数和逻辑运算的测试基准程序，测试基准程序来源于MediaBench[39]和MiBench[40]，测试基准程序对应的DFG包含数十个到数百个节点。实验测试基准程序的特征如表1所示。其中：DFG1用于评价子图枚举算法的数据流图的大小(节点数)；DFG2用于评价选择方法的数据流图的大小(节点数)。测试基准程序是由通用编译平台GECOS进行前端编译和模拟，高层次综合工具CtoS用于评价该方法对高层次综合性能的提升和面积的减少。其中，使用tutorial.lbr作为技术库，时钟频率设为50 MHz。本实验涉及到的测试基准程序包括：MP3、点积(Dot Product， DOTPRODUCT)、逆离散余弦变换(Inverse Discrete Cosine Transform， IDCT)、快速傅里叶变换(Fast Fourier Transform， FFT)、速率自适应调整(Automatic Rate Fallback， ARF)算法、无限脉冲响应(Infinite Impulse Response, IIR)、MESA(Mesa 3D是开放源代码的三维计算机图形库，本文采用求逆矩阵的测试基准程序)。

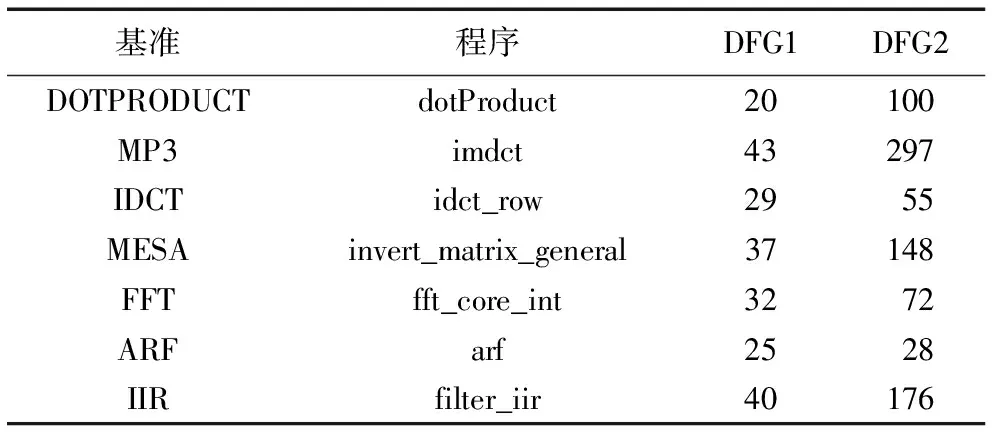
表1 基准程序特征

4.2 子图枚举效率比较

为了评价DFND算法的效率，将DFND算法与Balister等[28]提出的较新的TD(Transitive Digraph)算法以及Chen等[14]提出的经典CMS(Chen, Maskell, Sun)算法进行了比较，3种算法具有相同的约束条件。比较结果如表2所示，第一列代表测试基准程序；NV(Number node V)和NE(Number Edge)表示DFG中的节点数和边数；NS(Number Subgraph)表示枚举出的子图数；CT(Calculating Time)表示算法的运行时间，单位为ms。

从表2的结果可以看出，枚举所有的连通凸子图是一个复杂的计算问题。当DFG的规模较大时，枚举所有的连通凸子图是非常耗时的。例如，对于包含43个节点的基准程序MP3，DFND算法需要227 s枚举所有的连通凸子图。实验结果表明，DFND算法优于CMS算法和TD算法。与CMS算法相比，TD算法的枚举效率平均提升了44.5%；对于基准程序ARF，TD算法的枚举效率提升了49.5%。与CMS算法相比，DFND算法的枚举效率平均提升了83.8%。与TD算法相比，DFND算法的枚举效率平均提升了70.8%；对于基准程序MESA，DFND算法的枚举效率提升了73.1%。

表2 子图枚举算法的比较

4.3 面积减少率和性能提升率比较

为了评价本文提出的选择方法，应用程序的源代码和本方法产生的新代码分别作为高层次综合工具CtoS的输入。然后，使用高层次综合工具对两份代码分别进行高层次综合处理，表3中列Patterns和Matches分别表示候选模式和候选子图的数目。本文提出的基于关键路径的子图选择算法、基于出现频率的模式选择算法和基于最少子图数的选择算法分别表示为CS、PS、MS。符号X_P和X_M分别表示在不同选择方法下的模式数和子图数(如CS_P表示基于关键路径选择方法的模式数，PS_M表示基于出现频率的模式选择方法的子图数。此外，实验中子图节点数不超过6)。

表3 选择的模式和子图的数目

相比传统的高层次综合，本文提出的3种不同的子图选择方法对面积减少的结果如图9所示。其中，图9中的平均值表示对于7个基准程序的平均面积减少量。实验结果表明，不同的基准程序面积减少不相同。对于基准程序MP3使用CS算法可以减少41.6%的面积，对于基准程序DOTPRODUCT只减少5.5%的面积。通过观察发现，两个基准程序对应的DFG形状有很大差别，基准程序DOTPRODUCT对应的DFG是一个树形图，而基准程序MP3对应的DFG是一个网状图。通常，网状图具有较高密度的内部数据流。由于内部数据流可以粗略地表示多路选择器的数目，从具有更多内部数据流的网状图当中提取自定义指令可以节省大量的多路选择器。总体上，PS算法较其他两种选择算法能减少更多的面积。

相比传统的高层次综合，本文提出的3种不同的子图选择方法对性能提升的结果如图10所示。使用不同的选择方法在性能提升方面有很大的差异：CS算法能较好地提升性能，而其他两种算法不能提升性能，甚至可能降低性能，这主要是因为CS算法评估了关键路径长度。实验结果表明，对于基准程序DOTPRODUCT使用CS算法的性能提升达59.4%，然而，对于基准程序IDCT的性能提升只有12.2%，因此对于不同的基准程序，性能提升的效果差异明显。

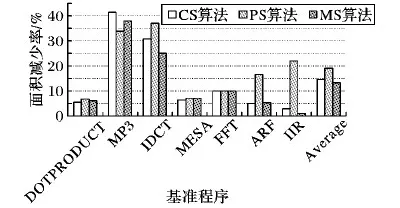
图9 3种选择算法减少面积结果比较

图10 3种选择算法提升性能结果比较

综上所述，相比传统的高层次综合：采用PS算法可平均减少19.1%的面积，最高可减少37.1%的面积；同时，采用CS算法平均可获得22.3%的性能提升，最高可达到59.4%的性能提升。相比Cong等[7-8]把自定义指令应用到高层次综合过程中的方法，本文方法能够在减少面积和性能提升之间提供更好的权衡。

4.4 代码减少率比较

为了评价代码的减少量，使用式(6)计算代码减少率：

RSize=((|G|-|G′|)/|G|)*100%

(6)

其中：|G|代表源代码中的运算指令数目，|G′|代表新代码运算指令的数目。

使用三种子图选择方法减少的代码量如图11所示，最少子图数目选择算法显著地减少了代码量。最少子图数目选择算法更倾向于选择较大的子图，而另外两种算法考虑到出现频率或关键路径倾向于选择较小的子图。例如，对于基准程序DOTPRODUCT，MS算法可减少81%的代码量。该算法可平均减少74%的代码量。通过减少代码量，高层次综合工具需要更短的时间去处理新代码，进而更快地产生电路设计方案。

图11 3种选择算法减少代码量结果比较

5 结语

本文利用自定义指令在专用硬件中可以提升性能、减少面积和减少代码量等优点，提出了面向高层次综合的自定义指令的自动识别方法。该设计方法克服了现有研究必须在高层次综合过程中识别自定义指令的限制。本文的DFND子图枚举算法可通过修改约束条件灵活地枚举出满足用户需求的子图。该算法以一种节点删除技术使得一个子图只被识别一次，显著地降低了枚举算法的运行时间。此外，不同的选择方法使高层次综合在解决性能和能耗问题上具有一定的应用价值，并且CS算法在面积减少、性能提升和代码量减少之间提供了很好的折中。

针对PS算法和MS算法对部分基准程序会带来负性能提升的问题。下一步的工作是结合PS、MS、CS三种算法的优点改进子图算法的功能函数，使子图选择算法能够更好地权衡性能、面积和代码量。