三种q-算子的推广

黄代萍

(重庆师范大学 数学科学学院，重庆 401331)

q-级数的研究始于1748年，经过多年的发展已较为成熟，其应用十分广泛，研究方法也多种多样.常见的有组合方法、解析方法和算子方法，其中算子方法对q-级数的研究起着至关重要的作用.算子方法的发展历史悠久.Rogers[1]用q-导数算子构造了两个q-指数算子来研究q-级数的某一性质，Chen Y C等[2]重新发现了Rogers的两个指数型算子，并给出了具有重要影响的两个算子恒等式；Fang J P[3]和Chen Y B等[4]利用参数扩充技巧先后构造了新的q-指数算子和Cauchy算子；张之正等[5]和Li N N等[6]又分别引入了双参数有限q-指数算子和三参数广义q-指数算子；受文献[2]的启发，Jia Z Y[7]将算子方法与q-移位阶乘的齐次形式[8]相结合，得到了新的q-指数算子恒等式.在已有的文献中，考虑到对Cauchy算子、双参数有限q-指数算子以及三参数广义q-指数算子应用Jia Z Y[7]的方法进行类似推广的研究较少，为进一步丰富算子理论，本文就此展开了研究.

1 预备知识

多重q-移位阶乘记作:(a1,a2,…,am;q)n=(a1;q)n(a2;q)n…(am;q)n.其中n为整数或.

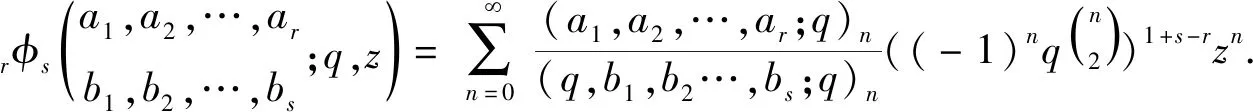
2 三种算子的推广

2.1 Cauchy算子的推广

上述算子就是Cauchy算子，可看作是Rogers[1]一个算子的推广.接下来，将给出Cauchy算子的一些性质.

定理1[4]若max{|bt|,|bs|,|ct|,|cs|}<1，则:

(1)

定理2[4]若max{|bt|,|bs|,|ct|,|cs|}<1，则：

(2)

在文献[7]中，Jia Z Y通过对文献[2]的结果的推广，得到了新的q-指数算子恒等式，在此基础上，导出了Cauchy算子的推广形式.

定理3 若max{|as|,|aω|,|ds|,|dω|}<1，且ω≠0，则：

(3)

其中Pn(a,b)=(a-b)(a-bq)…(a-bqn-1),P0(a,b)=1.

(4)

(5)

(6)

由式(2)知:

(7)

将式(7)代入式(8)，化简可得证.

当n=0时，定理3即为定理2，则可把定理3视为定理2的推广.

在式(3)中，令v=s，可推导出定理3的如下结果.

推论1 若max{|aω|,|dω|}<1，且ω≠0，则：

(8)

推论2[11]若max{|aω|,|dω|}<1，则：

(9)

在文献[11]中，陈永兵利用q-Leibniz公式得到了上述推论，下面将给出另一种证明方法.

证明首先给出Sears终止型的3φ2变换公式的一个变形[9]：

(10)

在式(10)中，用aω,dω,c,bdω分别替换a,b,e,d，有：

(11)

在式(11)中，令c=0，化简可得证.

2.2 双参数有限q-指数算子和三参数广义q-指数算子的推广

双参数有限q-指数算子[5]和三参数广义q-指数算子[6]分别定义为：

接下来，将分别给出双参数有限q-指数算子及三参数广义q-指数算子的一个重要性质.

定理4[5]若max{|as|,|at|}<1，则：

(12)

定理5[6]若max{|as|,|at|}<1，则：

(13)

在这一小节中，主要导出了双参数有限q-指数算子和三参数广义q-指数算子的推广形式.

定理6 若max{|as|,|aω|}<1，且ω≠0，则：

(14)

证明方法与定理3相同，下面给出具体的证明过程.

(15)

由式(12)知：

(16)

将式(16)代入式(15)，化简可得证.

当n=0时，定理6简化为定理4，即定理6是定理4的推广.

在文献[6]中，Li N N等已推导出以下恒等式，将给出其证明过程.

定理7[6]若max{|as|,|aω|}<1，且ω≠0，则：

(17)

(18)

由式(13)知：

(19)

将式(19)代入式(18)，化简可得证.

在式(17)中，令v=s，可得到以下结果.

推论3 对|aω|<1，且ω≠0，则：

(20)

2.3 推广后算子的简单应用

这一节中，将给出q-二项式定理的两个推广形式.

定理8 对max{|d|,|cd|,|bcd|,|x|}<1，且a≠0,c≠0，则：

(21)

证明q-二项式定理可以改写为：

(22)

对式(22)两边的变量x应用算子T(b,d;Dq)，有：

(23)

由式(8)和式(2)知：

(24)

(25)

将式(24)，(25)代入式(23)，化简可得证.

定理9 对|x|<1，且c≠0，则：

(26)

(27)

由式(20)和式(13)知：

(28)

(29)

将式(28)、(29)代入式(27)，化简可得证.

3 结语

在已有的成果基础上，为进一步得到新的结果，引入了三种q-算子，并将其与q-移位阶乘的齐次形式联系起来，从而推导出了一系列新的恒等式.此外，还得到了关于q-二项式定理的推广，所得结果在一定程度上对q-级数的研究起着推动作用.