实值函数近似鞍点集的连续性

王衍程，王 梅，刘 雷，李小兵

(重庆交通大学 数学与统计学院，重庆 400074)

鞍点问题在数学规划和博弈论的研究中占有非常重要地位.它为极大极小问题、拉格朗日对偶问题、变分不等式、Nash均衡问题的研究提供了有效地表述形式和基本工具.目前鞍点问题的理论研究主要是集中在鞍点的存在性[1-9].随着向量优化的发展，在适当的条件下，学者们研究得到了大量的关于向量值函数锥鞍点存在性的结论[6，8-10].

受上述研究结果的启发，主要研究标量值函数的含参鞍点问题.在大多数情况下，由于实际问题中数据具有不确定性，优化模型可能不存在精确解.因此，需要利用近似解来解决这些问题.本文，主要分析参数鞍点问题近似鞍点集的连续性.具体结构如下：首先，提出扰动鞍点问题，与含参近似鞍点集、辅助近似参近似鞍点集的定义，并回顾了一些集值映射相关概念和性质；然后，利用一些类似于文献[25]的技巧，在适当的条件下讨论了鞍点问题近似解的Hausdorff连续性.

1 模型描述及预备知识

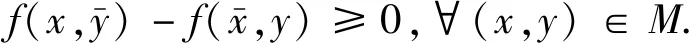
其中f:C×D×Λ→为实值函数，是非空凸集值映射并且M(Λ):={C(λ)×D(λ)|λ∈Λ}.

在优化理论与应用中，通常很难用数值算法得到优化模型的精确解，因此往往考虑优化模型的近似解.本文将考虑受到扰动鞍点问题的近似解的一些拓扑性质.为此，任取ε∈+(+表示非负实数集)以及λ∈Λ，接下来分别定义扰动鞍点问题的ε-近似鞍点集与辅助ε-近似鞍点集：

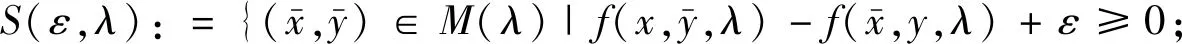
本文主要考虑拓扑性质：当参数λ和ε变化时，ε-近似鞍点集S(ε,λ)的稳定性(Hausdoff连续性).

下面，先介绍一些集值映射的相关知识.

1) 在x0∈X处Hausdorff上半连续(简写为H-上半连续)，若对于Y中的任意邻域，X中存在x0的邻域N(x0)，使得对任意的x∈N(x0)都满足：Q(x)⊂Q(x0)+.

2) 在x0∈X处Hausdorff下半连续(简写为H-下半连续)，若对于Y中的任意邻域，X中存在x0的邻域N(x0)，使得对任意的x∈N(x0)都满足：Q(x0)⊂Q(x)+.

3) 在x0∈X处Berge上半连续(简写为B-上半连续)，若对于满足Q(x0)⊆U的每一个开集U，X中存在x0的邻域N(x0)，使得对任意的x∈N(x0)都满足：Q(x)⊆U.

4) 在x0∈X处Berge下半连续(简写为B-下半连续)，若对于满足Q(x0)∩U≠φ的每一个开集U，X中存在x0的邻域N(x0)，使得对任意的x∈N(x0)都满足：Q(x)∩U≠φ.

若Q在x0处B-下半连续且B-上半连续，则称Q在x0处B-连续.同理，若Q在x0处H-下半连续且H-上半连续则称Q在x0处H-连续.

1) 若Q在x0处B-上半连续，则Q在x0处H-上半连续.

2) 若在x0处H-上半连续，并且Q(x0)是紧值的，则Q在x0处B-上半连续.

3) 若Q在x0处H-下半连续，则Q在x0处B-下半连续.

4) 若Q在x0处B-下半连续，并且Q(x0)的闭包clQ(x0)是紧值的，则Q在x0处H-下半连续.

1) 若Q在Λ上是紧值的，则Q在x0处B-上半连续的充要条件为：对X中任意的收敛序列xn→x0，任意序列yn∈Q(xn)，存在序列{yn}的子列{ynk}，y0∈Q(x0)，使得ynk→y0.

2)Q在x0处B-下半连续的充要条件为：对任意的收敛序列xn→x0，y0∈Q(x0)，存在序列{yn}⊂Q(x0)，使得yn→y0.

下面给出二元函数的凹性与凸性的定义.

定义2[29]假设C，D分别是X与Y中的非空凸子集.

1) 若对于∀x1,x2∈C，∀y∈D，∀t∈(0,1)，满足：

f(tx1+(1-t)x2,y)≤tf(x1,y)+(1-t)f(x2,y).

(1)

则称实值二元函数f:X×Y→在C上关于x是凸的，反之亦然.

2) 若对于∀x∈C，∀y1,y2∈D，∀t∈(0,1).满足：

f(x,ty1+(1-t)y2)≥tf(x,y1)+(1-t)f(x,y2),

(2)

则称实值二元函数f:X×Y→在D上关于y是凹的，反之亦然.

3) 若f既在C上关于x是凸的，又在D上关于y是凹的，则称f在C×D上是凹-凸的.

2 主要结果

考虑鞍点集S(ε,λ)在考虑点(ε0,λ0)附近的变化情况,在接下来的讨论中，均假设S(ε,λ)在点(ε0,λ0)的某个邻域内是非空的.

定理1 假设下列条件成立：

1)C(Λ)与D(Λ)是有界的；

2) 对于∀λ∈Λ，f(·,·,λ)在C(Λ)×D(Λ)上是凹-凸的.

则对于X中的任意闭凸零邻域,存在ε0的邻域V,对于∀λ∈Λ，∀ε∈V,满足:

S(ε0,λ)⊂S(ε,λ)+，S(ε,λ)⊂S(ε0,λ)+.

(3)

证明因为C(Λ)与D(Λ)是有界的，不难得出M(Λ)也是有界的.于是，对于X中的任意闭凸零邻域,存在ρ>0，使得:

M(Λ)-M(Λ)⊂ρ.

(4)

对于∀η∈(0,ε0)，∀ε1,ε2∈(ε0-η,ε0+η),其中ε1<ε2.任取(x1,y1)∈S(ε1,λ)，则:

f(x,y1,λ)-f(x1,y,λ)+ε1≥0,∀(x,y)∈M(λ).

于是，有:

f(x,y1,λ)-f(x1,y,λ)+ε2=f(x,y1,λ)-f(x1,y,λ)+ε2+(ε1-ε2)≥0.

因此，(x1,y1)∈S(ε2,λ)，且S(ε1,λ)⊂S(ε2,λ).进而对于∀ε∈[ε0-η,ε0+η]，有:

S(ε0-η,λ)⊂S(ε,λ)⊂S(ε0+η,λ).

(5)

(6)

事实上，任取(x1,y1)∈S(γ,λ)和(x2,y2)∈S(ε2,λ).根据式(1)和式(2)，可得:

(7)

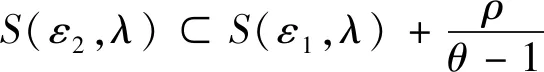
(8)

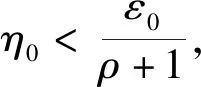
(9)

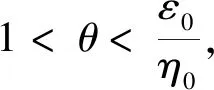
S(ε0,λ)⊂S(ε,λ)+.

S(ε,λ)⊂S(ε0,λ)+.

综上所述，式(3)成立.

引理3 令ε>0，λ∈Λ，若C(λ)与D(λ)在λ处B-上半连续并且有紧值，则S(ε,λ)在M(Λ)上是紧集.

证明由于C(λ)与D(λ)是紧子集，因此只需要证明S(ε,λ)是闭集即可.取(xn,yn)∈S(ε,λ)满足(xn,yn)→(x0,y0)，那么对任意的x∈C(λ)，y∈D(λ)，有:

f(x,yn,λ)-f(xn,y,λ)+ε≥0.

因为C(λ)与D(λ)在λ处B-上半连续并且有紧值，则(x0,y0)∈C(λ)×D(λ).因此对任意的x∈C(λ)，y∈D(λ)，有:

对对照组提供开腹手术方法治疗。首先,为患者提供硬膜外麻醉处理,取3-6cm的麦氏切口,然后找到阑尾,若系膜相对较为厚,则必须要分次进行结扎[2];若系膜属于正常范畴,则在患者的阑尾根部采用血管钳进行戳孔,在完成带线结扎处理以后,然后再切断系膜;把长度为0.5cm的阑尾结扎线留出来,选择使用碘酒进行消毒处理,之后实行打结操作。最后,将切口进行缝合处理,然后进行消毒包扎,结束手术操作。

f(x,y0,λ)-f(x0,y,λ)+ε≥0,

即(x0,y0)∈S(ε,λ).

定理2 假设下列条件成立：

1) 若C(·)与D(·)在λ0处B-连续并且紧值的；

2) 存在λ0的邻域N(λ0)，使得f(·,·,λ)在C(N(λ0))×D(N(λ0))×N(λ0)连续且是凹-凸的.

则存在ε0的邻域V使得，∀ε∈V，S(ε,·)在λ0处H-连续.

证明首先，证明S(ε,·)在λ0处H-上半连续.根据引理1(1)，只需证明S(ε,·)在λ0处B-上半连续即可.反设S(ε,·)在λ0处不是B-上半连续的，即存在S(ε,λ0)的邻域U，λn→λ0，(xn,yn)∈S(ε,λn)，但(xn,yn)∉U.根据S(ε,λn)的定义，存在xn∈C(λn)，yn∈D(λn)且λn→λ0，使得：

f(x,yn,λn)-f(xn,y,λn)+ε≥0,∀(x,y)∈M(λ).

(10)

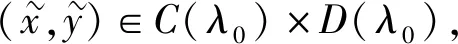
(11)

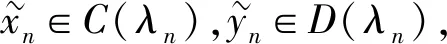
又因为f在C(N)×D(N)×{λ0}上是连续的，则：

与式(11)矛盾.

因此S(ε,·)在λ0处B-上半连续，那么S(ε,·)在λ0处也是H-上半连续的.

(12)

因为C(·)与D(·)在λ0处B-上半连续并且有紧值，则存在{xn}的子序列{xnk}和{yn}的子序列{ynk}，使得xnk→x，ynk→y，其中x∈C(λ0)，y∈D(λ0).根据式(12)可得:

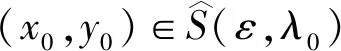
由引理1(4)可知，S(ε,·)在λ0处H-下半连续.

定理3 假设下列条件成立：

1)C(Λ)与D(Λ)是有界的；

2) 若C(·)与D(·)在λ0处B-连续并且有紧值；

3) 存在λ0的邻域N(λ0)，使得f(·,·,λ)在C(N(λ0))×D(N(λ0))×N(λ0)连续且是凹-凸的.

则ε-近似鞍点集S(·,·)在(ε0,λ0)处H-连续.

证明显然，对于任意的零邻域,存在零邻域0⊂X，满足:

0+0⊂.

(13)

S(ε0,λ)⊂S(ε,λ)+0，S(ε,λ)⊂S(ε0,λ)+0.

(14)

再根据定理2可得，S(ε,·)在λ0处H-连续.因此，对于任意的ε∈V0，存在λ0的邻域N0，使得:

S(ε,λ0)⊂S(ε,λ)+0，S(ε,λ)⊂S(ε,λ0)+0，∀λ∈N0.

(15)

显然，(V0×N0)是(ε0,λ0)的邻域.结合式(13)，式(14)与式(15)可知，对于任意的(ε,λ)∈(V0×N0)，有:

S(ε0,λ0)⊂S(ε,λ)+，S(ε,λ)⊂S(ε0,λ0)+.

因此，S在(ε0,λ0)处H-连续.