基于观测器的Markovian跳变广义生物系统的滑模控制
王 静,张 翼
(沈阳工业大学 理学院,沈阳 110870)
广义系统也被称为奇异系统,是一种数学表示形式,是描述和研究实际模型的有力工具,因此,广义系统受到了越来越多学者的关注[1-3].而在系统参数扰动的情况下,广义系统就不具有结构的稳定性,而Markovian跳变系统能有效地描述这类参数扰动下结构的突变,Markovian跳变是一类特殊的随机系统,用来刻画系统的结构和参数随时间变化的系统[4-6].
近年来,将广义系统的相关理论应用于生物系统已成为许多学者的研究重点,在实际系统中,种群会受到诸多随机因素的影响,因此,研究随机广义生物系统的建模和稳定性分析具有重要的学术价值和实际意义[7-9].Zhang等[10]在广义生物系统方向的研究做出了贡献,并对种群在不同环境的影响下进行建模,以此来达到其环境的稳定性,在此之后很多学者对其进行深入研究,研究了污染环境中单一生物经济系统的建模和控制,且提出了一种新的随机平均方法来分析高斯白噪声激励下的冲击振动系统[11].Lee K等[12]给出了具有Markovian跳变的广义生物经济系统的随机最优保成本控制.总而言之,广义系统在生物经济领域的应用中有着广阔的前景.
滑模控制(SMC)作为一种非线性控制策略,具有响应快、速度快等优点,SMC能够克服系统的一些不确定性,对扰动和建模都具有较强的鲁棒性[13],且在系统处于滑模相位时能够完全补偿匹配的不确定性[14-17].SMC目前已经应用到很多复杂系统中,如广义系统、电力系统、生物系统等,并且SMC对各种复杂动力系统的相关介绍[18-19].概括来说,SMC就是通过设计SMC律,在有限的时间内将系统的轨迹驱动到预先设计的、具有稳定性等理想特性的滑动面中[20],给出了一种基于观测器的线性积分滑模控制方法,并且最终保持稳定.
本文主要研究的是基于观测器的Markovian的随机广义生物系统的变结构控制问题,将广义生物系统理论与T-S模糊规则相结合,将生物种群的密度控制在一个有界的范围内,并且消除系统中的一些不确定因素,建立T-S模糊模型,并提出了基于观测器的有限时间的模糊滑模控制方法,设计了一种模糊滑模控制器,以保证在规定时间之前的有限时间内到达滑模面.并且保证了观测器控制系统在到达阶段和滑动运动阶段同时具有有界性.
1 模型建立
由于种群在不同阶段的生理机能有着差别,在不同程度上会影响种群的生存和灭绝,其阶段结构的种群模型可表示为:
(1)
其中x1(t)表示幼年种群密度,x2(t)表示成年种群密度,a1表示幼年种群的出生率,b表示幼年种群转化为成年种群转化率与死亡率之和,δ表示幼年种群转化为成年种群转化率,β表示成年种群的内部竞争系数.
在模型(1)的基础上,为了使具有阶段结构的种群模型更具有实际意义,根据Gordon理论,建立广义生物系统模型如下:
(2)
其中x3(t)表示整个养殖过程的成本,a2表示贷款用来购买幼年种群的比例,c1表示基本成本,E(t)表示对成年物种x2(t)的单位密度捕获量,ρ表示捕获单位成年种群的价格系数,c2表示贷款的系数,d1表示贷款利率,c3表示利润里面用来偿还贷款的部分,cE(t)代表总成本,m(t)表示经济利润.

定理1 若系统(2)在正平衡点P*处是稳定的,则满足以下不等式:
其中:
证明系统(2)的Jacobian矩阵可表示为:

λ4+Λ1λ3+Λ2λ2+Λ3λ+Λ4=0
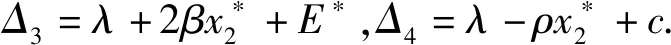
当满足下列不等式时:
根据Routh-Hurwitz定理可知,系统(2)在平衡点P*处是稳定的.
在实际生活中,成熟种群的选择并不是固定的,它受到多种因素的影响,如生产成本、利率、比较产量和汇率等.因此,假设成年种群的市场价格取有限集S={1,2,3,…,N}遵循Markovian跳变过程,且转移概率矩阵为:Π≜{λpq}.

则系统(2)可写为:
(3)
当m(t)=0时,在正平衡点P*处做如下线性变换:
一般情况下,种群的出生率和幼年到成年的转化率均会受外界环境和人类活动的影响,考虑到诸多因素的影响,在系统(3)上加入外部扰动和控制输入,则有:
其中w(t)表示外部扰动,u(t)表示控制输入,b11,b12,b13,b14表示外部扰动的系数,系统可以写成:
其中:
令:
运用最大值最小值原理,z1(t),z2(t)可表示为:

其中Mi1+Mi2=1,i=1,2,Mij(i,j=1,2)为隶属度函数,利用T-S模糊方法,将系统写为:
上述广义模糊控制系统包含4个模糊规则,若将模糊规则推广到正整数r个控制系统,令p=rt,则有:
Ai(rt)=Ap,i,Bi(rt)=Bp,i,Jw,i(rt)=Jp,wi.
从而:
(4)
其中:
其中ωij(ζj(t))是ζj(t)在模糊集wij的隶属度.
为了便于观测器设计,在系统(4)中加入输出向量:
(5)
其中y(t)∈Rp是控制输出,Cp是具有适当维数的常数矩阵,当系统状态不完全可访问时,状态反馈控制器可能失效.因此,给出如下滑模观测器:
(6)

(7)
其中W(t)被作为扰动,且满足:

(8)
定义1[21]若给定两个标量c1>0和c2>0且c1 (9) 则系统(6)是关于{c1,c2,T,R,d}时域有界的. 定义2[22]考虑李雅普诺夫函数V(ζ(t),rt,t≥0),对ζ(t)进行两次微分,则无穷小微分算子LV(t)可被定义为: (10) 引理1[23]给定任意向量ζ,y∈Rn×n和0 2ζTy≤ζTPζ+yTP-1y. (11) 在观测器(6)的基础上,给出模糊积分滑模面函数为: (12) 其中G∈Rm×n,且GBp,i是非奇异的,选取Kp,i∈Rm×n使得Ap,i+Bp,iKp,i是Hurwitz矩阵. 接下来,将设计一个基于观测器的滑模控制器,使滑模面s(t)=0在给定时间T内可达,使得系统的状态轨迹在有限时间内能够驱动到滑模面上,且在随后的时间保持在滑模面上. 定理2 给定观测器系统(6)和滑模面函数(12),当滑模面s(t)=0在时间T*内可达,滑模控制律可表示为: (13) 证明选取Lyapunov函数: (14) 由式(6)和式(12)可知: 因此,可知式(14)的无穷小微分算子为: (15) (16) 因此,滑模面s(t)=0在时间T内可达. 将式(13)代入式(6)中,可得闭环系统为: (17) 定理3 若存在矩阵Pp>0,Q1>0和Q2>0,给定正常数μ>0,γ>0,和c′>0且满足以下条件: Q1-12m2γI≥0, (18) Q2-3m2γI≥0, (19) (20) (21) 其中: 和 证明选择Lyapunov函数: (22) 由定义2和文献[24]中的无穷小微分算法可知: (23) 令PpLp,i=Hp,i,由式(20)可得到: LV(t)-αV(t)-βWT(t)WT(t)-γ(ρ(t)+δ)sgn(s(t))T(ρ(t)+δ)sgn(s(t))≤ ηT(t)Mp,iη(t)<0. (24) 由式(24)可知: e-αtε[LV(t)-αV(t)]≤e-αtε[βWT(t)WT(t)+γ(ρ(t)+δ)sgn(s(t))T(ρ(t)+δ)sgn(s(t))]. (25) 对式(25)从0到t进行积分有: (26) 由式(22)可知: (27) (28) 其中有: (29) 由式(27)~(29)可知: (30) ∀t∈[0,T*],由式(21)可知: 基于滑模面(12)和观测器(6),可知: (31) (32) 把式(32)代入式(6)中,可以得到滑动模态方程为: (33) 其中Ip=I-Bp,i(GBp,i)-1G. 定理4 若存在矩阵Pp>0,Hp,i>0和标量μ>0,γ>0,对于任意p∈S满足以下条件: (34) (35) 其中λ1,λ2和c′在定理2中已经给出: 证明选取Lyapunov函数: (36) 其无穷小微分算子为: (37) (38) 由式(34)可知: LV(t)-αV(t)-βWT(t)WT(t)≤ηT(t)Mp,iη(t)<0. (39) 因此∀t∈[0,T**],由式(35)可知: 从实际情况出发,由于物种受外界影响过多,深入物种对本土种群及人类带来的影响,同时考虑经济因素,利用模糊方法研究了具有Markovian跳变广义生物系统的有限时间滑模控制问题,将广义生物系统理论与T-S模糊规则相结合,并且消除系统中的一些不确定因素,建立T-S模糊模型,并设计滑模观测器,在此基础上,基于模糊观测器构造积分滑动曲面. 其次,设计一种基于观测器的滑模控制律,以保证给定滑模面在规定时间内有限时间可达.最后通过时域界性分析,分别在到达阶段和滑动模态阶段进行了有界性性能分析.这对于生态系统的持续良好循环,改善环境以及长期稳定地获取经济利益产生了积极而又深远的影响.
2 主要结果
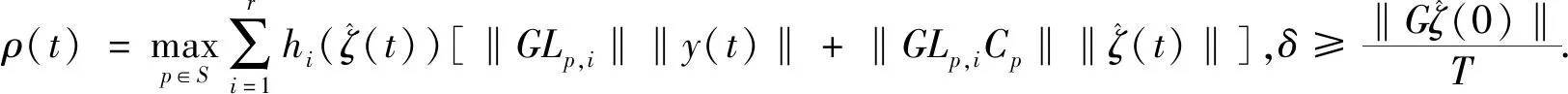
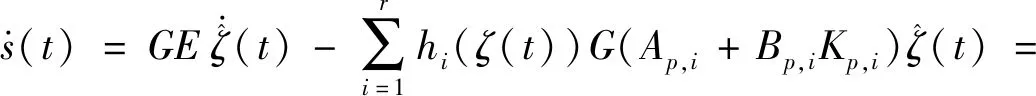

3 时域有界性分析
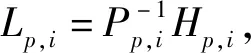
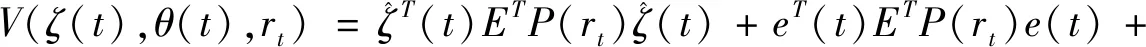


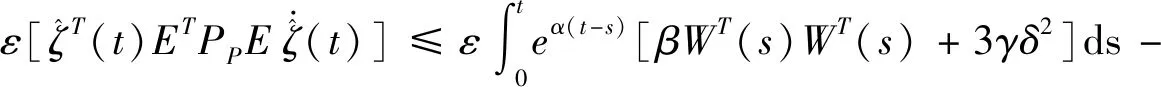




4 滑动模态的时域有界分析
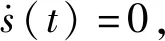
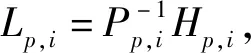

5 结论

