L-拓扑空间广义模糊半紧性

徐振国, 刘梦国

(1.国家科技基础条件平台中心，北京 100038; 2.沈阳市同泽高中，辽宁 沈阳 110011)

1 预备知识

文献[1-2]在L-拓扑空间中给出了一种新的紧性，该紧性是通过不等式来刻画的且不依赖于格L的结构，不要求L具有分配性.

文献[3]中作者给出广义半开L-集、广义半闭L-集和广义半不定映射的概念.

本文借助于广义半开L-集和不等式，给出广义模糊半紧性，这里L是完备的de Morgan代数，这个定义不依赖于L的结构，并且不要求L具有分配性.广义模糊半紧性同样可以借助广义半闭L-集和不等式来刻画.当L是完全分配的de Morgan代数时，给出它的许多等价刻画.

对于子集Φ⊂LX，2(Φ)记为Φ的所有有限子族之集.

定义1[3]令(X,T)是一个L-拓扑空间且A∈LX.则A称为广义半闭L-集(简记为gs-闭L-集)，如果对于满足A≤U的半开L-集U，有cl(A)≤U.A称为广义半开的(简记为gs-开)，如果A′是gs-闭的.

GSO(X) 和GSC(X) 分别记为X上所有广义半开L-集和广义半闭L-集之集.

定义3[1-2]令(X,T)是一个L-拓扑空间且A∈LX.则G称为模糊紧的，如果对于U⊂T，有

2 广义模糊半紧L-集

定义4令(X,T)是L-拓扑空间且G∈LX.则G称为广义模糊半紧的，如果对每族U⊂GSO(X)，有

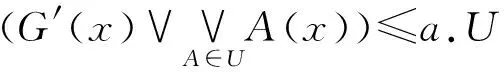
显然，G的广义半开强a-shading是G的广义半开a-shading.

由定义4和定义5有下面的结果.

定理1令(X,T)是L-拓扑空间且G∈LX.则G是广义模糊半紧的当且仅当对任意的a∈L{1}，G每个广义半开强a-shadingU有有限子族V是G的广义半开强a-shading.

此外，由定义4和逆序对合对应有如下定理.

定理2令(X,T)是L-拓扑空间且G∈LX.则G是广义模糊半紧的当且仅当对每个子族P∈GSC(X)，有

显然，G的广义半闭强a-remote族是G的广义半闭a-remote族，P是G的广义半闭强a-remote族当且仅当P′是G的广义半闭强a-shading.

由定理2，有下面的定理.

定理3令(X,T)是L-拓扑空间且G∈LX.则G是广义模糊半紧的当且仅当对任意的a∈L{0}，G的每个广义半闭强a-remote族P有有限子族F是G的广义半闭强a-remote族.

定理4令L是完备的Heyting代数.如果G和H是广义模糊半紧的，则G∨H是广义模糊半紧的.

证对任意的P∈GSC(X)，由定理2有

这证明了G∨H是广义模糊半紧的.

定理5如果G是广义模糊半紧L-集，H是广义半闭L-集，则G∧H是广义模糊半紧L-集.

证因为G是广义半闭L-集，对于任意的P∈GSC(X)，由定理2，有

这证明了G∧H是广义模糊半紧L-集.

证对任意的P∈GSC(X)，由引理1和G的广义模糊半紧性，有

3 广义模糊半紧性的刻画

这节中，假设L是完全分配的de Morgan代数.给出广义模糊半紧性的一些刻画.

定理7令(X,T)是L-拓扑空间且G∈LX.则下面条件是等价的.

(1)G是广义模糊半紧的；

(2)对任意的a∈L{0}，G的每个广义半闭强a-remote族P有有限子族F是G的广义半闭强a-remote族；

(3)对任意的a∈L{0}，G的每个广义半闭强a-remote族P有有限子族F是G的广义半闭a-remote族；

(4)对任意的a∈L{0}，G的每个广义半闭强a-remote族P有有限子族F和b∈β*(a)使得F是G的广义半闭强b-remote族；

(5)对任意的a∈L{0}，G的每个广义半闭强a-remote族P有有限子族F和b∈β*(a)使得F是G的广义半闭b-remote族；

(6)对任意的a∈M(L)，G的每个广义半闭强a-remote族P有有限子族F是G的广义半闭强a-remote族；

(7)对任意的a∈M(L)，G的每个广义半闭强a-remote族P有有限子族F是G的广义半闭a-remote族；

(8)对任意的a∈M(L)，G的每个广义半闭强a-remote族P有有限子族F和b∈β*(a)使得F是G的广义半闭强b-remote族；

(9)对任意的a∈M(L)，G的每个广义半闭强a-remote族P有有限子族F和b∈β*(a)使得F是G的广义半闭b-remote族.

类似地，能够证明(2)⟹(6)⟹(7)⟹(8)⟹(9)⟹(1).

4 结 论

(1)G是广义模糊半紧的当且仅当对任意的P∈GSC(X)，有

(2)如果G和H是广义模糊半紧的，则G∨H广义模糊半紧的，这里L是完备的Heyting代数.

(3)如果G是广义模糊半紧L-集，H是广义半闭L-集，则G∧H是广义模糊半紧L-集.

(4)广义模糊半紧L-集在广义不定映射下是保持的，这里L是完备的Heyting代数.