Bloch型空间到加权Bloch型空间的Volterra算子
谭杏娟,谭海鸥
(五邑大学 数学与计算科学学院,广东 江门 529020)
Bloch型空间到加权Bloch型空间的Volterra算子
谭杏娟,谭海鸥
(五邑大学 数学与计算科学学院,广东 江门 529020)
给出并证明了从Bloch型空间Bα到加权Bloch型空间的Volterra算子有界性和紧性的充分必要条件.
Volterra算子;Bloch型空间;加权Bloch型空间;有界性;紧性
1 预备知识

设φ∈H(D),算子J定义为:
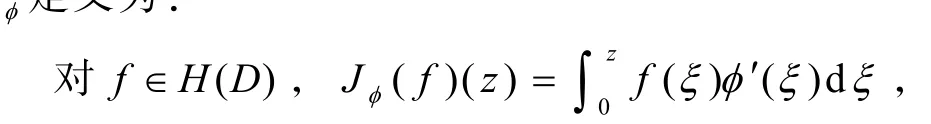
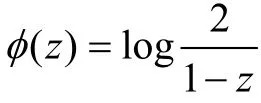
关于Volterra算子Jφ已有许多研究成果,如A. Aleman和A. J. Cima[2]讨论了当0 证明利用引理2. 1及Montel定理和定义[9]可证得. 定理3.2φ∈H(D),则Jφ是Bα到上的紧算子的充要条件是: 证明必要性 设J是Bα到上的紧算子, 由引理3.1知,这与Jφ的紧性矛盾. 这与Jφ的紧性矛盾. 这与Jφ的紧性矛盾. 由引理3.1知,Jφ是Bα到上的紧算子. 同理用类似方法可证明0<α<1和α=1的情况. 定理3.2证毕. [1]谭海鸥. 一类加权α-Bloch空间上复合算子的有界性和紧性[J]. 五邑大学学报:自然科学版,2004, 18(4): 7-10. [2]ALEMAN A, CIMA J A. An integral operator onpHand Hardy’s inequality[J]. J Anal Math, 2001, 85(1): 157-176. [3]ALEMAN A, SISKAKIS A G. An integral operator onpH[J]. Complex Variables Theory Appl, 1995, 28(2): 149-158. [4]ALEMAN A, SISKAKIS A G. Integration operators on Bergman spaces[J]. Indiana Univ Math J, 1997, 46(2): 337-356. [5]SISKAKIS A G, ZHAO Ruham. A Volterra type operators on spaces of analytic functions[J]. Contemporary Math, 1999, 232: 299-311. [6]瞿丹. Bloch型空间上的 Volterra算子[J]. 韩山师范学院学报,2008, 29(3): 9-11. [7]李颂孝. 有界对称域上加权Dirichlet空间上的加权复合算子[J]. 湖州师范学院学报,2003(6): 22-25. [8]ZHU Kehe. Operator theory in functions spaces [M]. 2nd ed. Washington: American Mathematical Society, 2007. [9]张南岳,陈怀惠. 复变函数论选讲[M]. 北京:北京大学出版社,1995. [责任编辑:孙建平] The Volterra Operator from Bloch Type Analytic Function Spaces to Weighted Bloch Type Analytic Function Spaces TAN Xing-juan, TAN Hai-ou In this paper, some necessary and sufficient conditions of Volterra operator from Bloch type analytic function spacesBαto weighted Bloch type analytic function spacesare given and proven. Volterra operator; Bloch type spaces; weighted Bloch type spaces; boundedness; compactness O174. 5;O177. 2 A 1006-7302(2010)02-0005-41 2009-12-15 谭杏娟(1982—),女,广东江门人,研究生,研究方向:复分析,E-mail: tina19821125@126. com;谭海鸥,教授,硕士,硕士生导师,通信作者,主要从事复分析方面的研究,E-mail: Hotan@wyu. cn.2Bα到的Volterra算子J的有界性φ


3Bα到的Volterra算子J的紧性φ

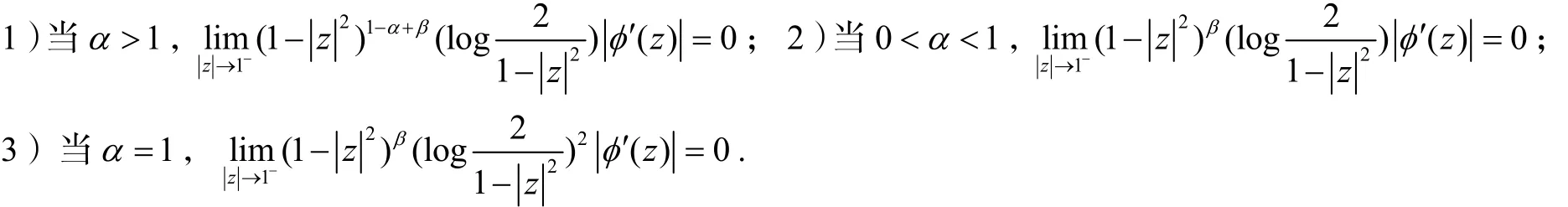
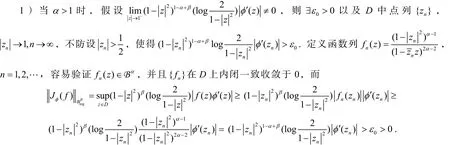
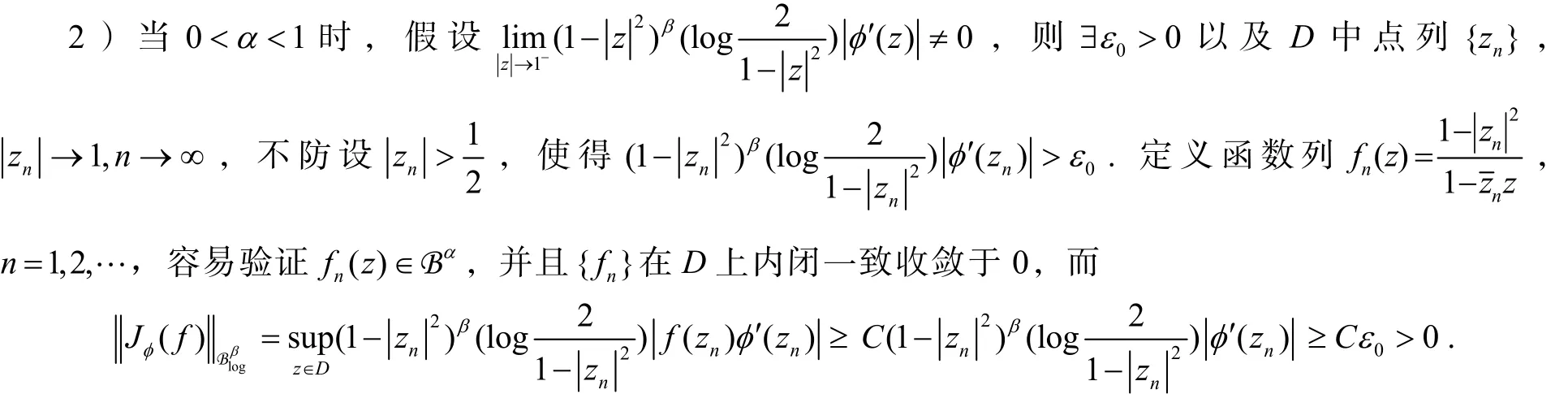
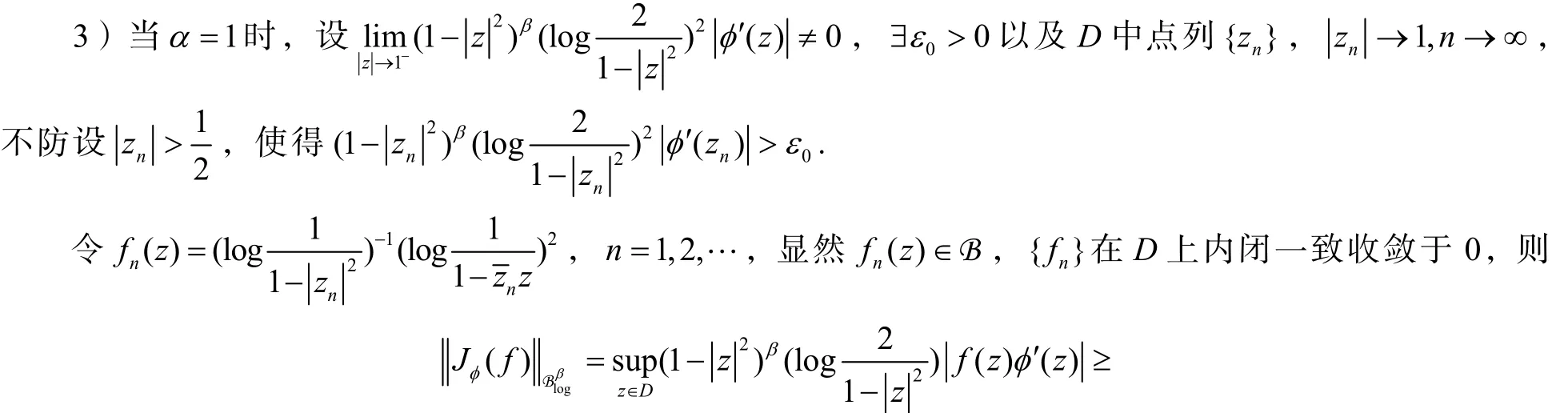
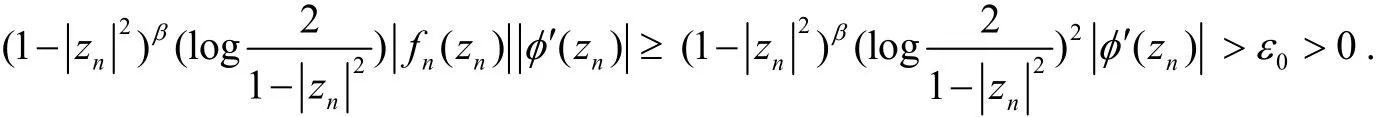

(School of Mathematics and Computational Science, Wuyi University, Jiangmen 529020, China)

