排列图的限制边连通度

邹婷婷，曾雪倩，李向军

(长江大学 信息与数学学院，湖北 荆州 434023)

在大规模多元信息处理系统中，元件故障不可避免，当故障发生时网络对某些条件性质的保持能力就是它的容错性能.在设计大规模网络时，高性能、低成本是最终目标.在选择互连网络的拓扑结构时，处理器之间的有效通信是衡量系统性能的一个重要标准，当处理器数目逐渐增多时，其发生故障的可能性也随之增加，不同处理器之间信息传递过程中的容错性便成为一个非常关键的问题，为此有必要考虑网络的容错性和可靠性.点连通度(记作κ(G))是使得G-T不连通的最小顶点子集T的基数；边连通度(记作λ(G))的定义类似，它是使得G-F不连通的最小边子集F的基数.但连通度假设任意顶点和任意边可以同时发生故障，在实际应用中并不能很好地反映网络的弹性，Harary针对这一弱点，引入了条件连通度的概念，对剩余的网络提出了一些附加要求[1].此后，Latifi等[2]在一定意义上推广了这一概念，通过限制每个顶点至少有h个无故障邻点，提出了h-限制连通度.在实际应用中，这些广义度量可以更准确地估计互连网络的容错性.

用无向图G=(V;E)表示互连网络的拓扑结构，图G的顶点V(G)代表系统中的元件，图G的边E(G)代表元件之间的物理连线[3].对于u∈V,u的度是与u关联的边数，记作d(u)，δ(G)表示图G的最小度.假设G为连通图，T是V(G)的子集，若G-T不连通且最小度至少为h，即δ(G-T)≥h，称T是图G的h-点割，h-限制点连通度(记作κh(G))是最小h-点割的基数.对于边故障的网络容错性刻画也有类似度量，F是E(G)的子集，若G-F不连通，且δ(G-F)≥h，称F是图G的h-边割，h-限制边连通度(记作λh(G))是最小h-边割的基数.显然有κ0=κ,λ0=λ.对有向图的点割研究也有不少学者关注[4-6]，本文的主要研究对象是无向排列图.在排列图的容错性研究方面，国内外学者对其点故障关注较多，Zhou等[7]、林丽美等[8]、Cheng等[9-10]学者在其限制连通度方面得到了部分重要结果；Wang等[11-12]、Lin等[13]、Lei等[14]、Xu等[15]等学者在子结构容错方面做了很好的工作.目前对排列网络边故障情况的分析和探讨还较少，而现实网络中连线故障是确实存在的，本文利用图结构分析方法对排列图An,2的边故障容错能力进行探索，当h≤3时确定其限制边连通度λh(An,2)，该结果可为进一步分析排列图的边故障容错能力提供借鉴.

1 预备知识

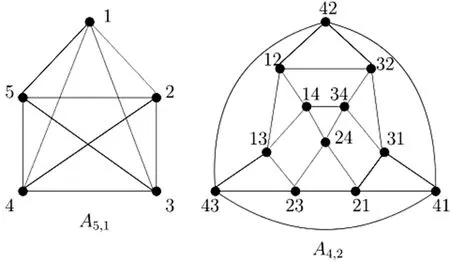
定义1[16]令n,k为两个整数，且1≤k

图1 排列图A5,1和A4,2Fig.1 The arrangement graphs A5,1 and A4,2

用Hi表示An,k一个顶点子集，它是第j(1≤j≤k)个位置元素pj为i(1≤i≤n)的排列.对顶点v∈Hi，v在Hi中的邻点称为内邻点，v在An,k-Hi中的邻点称为外邻点.

性质1[16]当2≤k

性质3[16]对于Hi中的j个顶点，它们有j(n-k)个不相交的外邻点.

2 主要结果

主要考虑排列图An,2的h-限制边连通度.

引理1 当0≤h≤n-2时，λh(An,2)≤(h+1)(2n-h-4).

证明不失一般性，在H1中取一个(h+1)-团(记为X)，F表示X与N(X)之间所有的边.由于An,2是2(n-2)-正则的，有|F|=2(n-2)(h+1)-h(h+1)=(h+1)(2n-h-4).

以下证明F是一个h-边割，令Y=G-X，证明δ(Y)≥h即可.如果j≠1，对于任意顶点u∈Hj，由于Hj是一个(n-1)-团，所以δY(u)≥δHj(u)=n-2≥h.对于任意顶点u∈H1-X,u有(n-2)个外邻点，从而有δY(u)≥n-2≥h，所以δ(Y)≥h.故F是一个h-边割，λh(An,2)≤|F|=(h+1)(2n-h-4).引理得证.

定理1 当h∈{1,2,3}，n≥h+2时，λh(An,2)=(h+1)(2n-h-4).

证明根据引理1，只需证明λh(An,2)≥(h+1)(2n-h-4).

令F是An,2的最小h-边割，只需证明|F|≥(h+1)(2n-h-4).

假定X是An,2-F中一个连通分支，Y=An,k-X，令Xi=X∩Hi,Yi=Y∩Hi.

令JX={i∈[n]:Xi≠∅},JY={i∈[n]:Yi≠∅},J0=JX∩JY；考虑这几个集合大小，令a=|J0|,b=|JX-J0|,c=|JY-J0|，则a+b+c=n.因为X与Y有对称性，不妨假设|JX|≤|JY|.由于Hi表示第j(1≤j≤2)个位置元素pj为i(1≤i≤n)的排列，可以选择某个j(1≤j≤2)使得|JX|尽可能大.

用EC表示∪j1∈JX-J0Hj1与∪j2∈JY-J0Hj2之间所有的边，对于j1∈JX-J0和j2∈JY-J0,Hj1与Hj2之间有n-2条相互独立的边，故|EC|≥bc(n-2).

用EI表示∪j3∈J0Xj3与∪j3∈J0Yj3之间所有的边，对于j3∈J0,由于Hj3同构于Kn-1，故|EI|≥a(n-2).由于F是边割，故EI⊂F.注意到EC⊂F，则有|F|≥|EC|+|EI|≥bc(n-2)+a(n-2)≥(a+bc)(n-2).

如果bc≠0，则有(a+bc)(n-2)≥(n-1)(n-2)，从而|F|≥(n-1)(n-2)≥(h+1)(2n-h-4).

下面假设bc=0，由|JX|≤|JY|有b=0，从而|JX|=|J0|=a.

下面考虑a

考虑函数f(a)=a(2n-3-a),则|F|≥f(a).易知f(a)在区间[1,n-2]单调增加，且f(n-1)=f(n-2).

h=1时，a≥2，根据f(a)在[1,n-2]单调性，有|F|≥f(a)≥f(2)=4n-10.

h=2时，如果a≥3，由f(a)单调性，可知|F|≥f(a)≥f(3)=6n-18.

h=3时，如果a≥4，由f(a)单调性可知|F|≥f(a)≥f(4)=8n-28.

所以h=1，2，3时都有λh(An,2)≥(h+1)(2n-h-4)，定理得证.

3 结语

研究了排列图An,2的边故障容错能力，对n≥3确定λ1(An,2)=4n-10，对n≥4确定λ2(An,2)=6n-18，对n≥5确定λ3(An,2)=8n-28.当h≥4时确定λh(An,2)，以及对k≤n-2，h≤n-k确定λh(An,k)是值得进一步研究的问题.