Carmichael猜想的一个标注
王恒洲, 史三英
(合肥工业大学 数学学院,安徽 合肥 230601)
对于任意整数x,文献[1]证明了关于未知数n的方程φ(n)=x解的个数不为1,但是文献[1]的证明被发现存在错误,这个断言便被称为Carmichael猜想;文献[2]证明了当x<1037时,该猜想是成立的;文献[3]将这个界提高到10400;文献[4-5]分别将上界提高到1010 000、10107。目前10108仍是最好的结果。
文献[6]证明了反例的一个充分条件,即如果对于每一个使得p-1整除φ(n)的素数p都有p2|φ(n),那么n就是一个反例。
文献[7]证明猜想成立当且仅当
其中
E1(x)=#{n|1≤n E(x)=#{n|1≤n A(m)=#{n|φ(n)=m}。 文献[7]还证明了E1(x)=101010。 关于A(m)值域的研究是Carmichael猜想的一个重要的延伸课题。文献[8]证明了任意非1的正整数都属于A(m)的值域。 本文中p和q总是表示素数,P(x)表示x的所有素因数集,S(x)表示满足p-1整除x的全体p的集合。定义vp(x)为p整除x的最高指数,即pvp(x)‖x。 定义1 若T(x)⊂S(x),并满足: 当p∈T(x)∩P(x)时,有 当p∈P(x)-T(x)时,有 则称T(x)为S(x)的一个φ-子集。 定义N(x)是方程φ(n)=x的关于未知数n的解数,则Carmichael猜想成立等价于N(x)≠1。本文将证明下面的定理。 定理1N(x)等于S(x)的φ-子集的个数。 定理2 Carmichael猜想的成立当且仅当该猜想在集{24337243k,k为任意正整数}上成立。 (1) 下面将证明对于S(x)不同的φ-子集,都能找到不同的n,满足φ(n)=x。假设T(x)是S(x)的一个φ-子集,由定义可得: 由算术基本定理可得,当T1(x)≠T(x)时,存在n1≠n,满足φ(n1)=φ(n2)。 由上述可知,对于S(x)不同的φ-子集,都能找到不同的n满足φ(n)=x。 x=φ(n)= 令T′(x)={p1,p2,…,pt},可得: 对于p∈P(x)∩T′(x),则有: 对于p∈P(x)-T′(x),则有: 则由定义1可知T′(x)是S(x)的φ-子集。 由算术基本定理可知,若存在一个不等于n的m满足φ(m)=x,则S(x)存在一个不等于T′(x)的φ-子集。 由(1)、(2)可得,对于任意满足φ(m)=x的正整数n,都能唯一地构造S(x)的φ-子集。 推论1 若偶数x满足S(x)=P(x),且当p∈P(x)时,有 则N(x)=1。 证明由S(x)=P(x)条件可知,S(x)是本身的一个φ-子集。对于S(x)的任意真子集S1(x),令p0∈P(x)-S1(x),可得: 因此,S(x)的任意子集都不会是S(x)的φ-子集。故S(x)只有一个φ-子集,即N(x)=1,也就是说x=φ(n)是Carmichael猜想的一个反例。 令T(x)是S(x)的一个φ-子集,ρ是T(x)∩P(x)子集,且满足: 若p∈T(x)∪{q0}∩P(x),则 vp(q0-1)=0。 由定义1可知,T(x)∪{q0}也是S(x)的φ-子集。 由上述可知,当S(x1)⊄T(x)时,可以通过添加一个元素来生成新的φ-子集。 定义Tρ(x)={q|P(q-1)⊂ρ}∩T(x)。当Tρ(x)⊄ρ时, 取q0∈Tρ(x)-ρ,易证T(x)-{q0}也是S(x)的φ-子集,这是因为对于p∈P(x)∩(T(x)-{q0}),有 对于p∈P(x)-(T(x)-{q0}), 定义1得到满足。 综上所述,当Tρ(x)⊄ρ时,可以从φ-子集删除一个元素生成新的φ-子集。 显然可得,当S(x)存在一个满足以上2个条件的φ-子集时,N(x)≠1。下面将研究不满足上述2个条件的φ-子集,即无法通过上述2个方法生成新的φ-子集的T(x)。 为了证明定理2,需要先证明下面的2个引理。 引理1 Carmichael猜想成立当且仅当猜想在集合S(x)上成立。 (1) 假设S(x)只有一个φ-子集T(x),则T(x)无法通过上述删除一个元素生成新的φ-子集。 当Tρ(x)=T(x)时,有 T(x)=Tp(x)⊂ρ=P(x), P(x)⊂ρ⊂T(x), 因此x∈T1。 当Tρ(x)≠T(x)时,令 由x1的定义可得: Tp(x)⊂ρ, P(x1)⊂ρ⊂T(x), S(x1)⊂Sp(x), 定义Sρ(x)={q|P(q-1)⊂ρ}∩S(x),则有: S(x1)∩P(x1)⊂T(x)∩Sρ(x)=Tρ(x)。 另一方面,因为Tρ(x)⊂S(x1)∩P(x1),所以Tρ(x)=S(x1)∩P(x1)。这说明Tρ(x)也不能通过删除一个元素来生成新的φ-子集。于是可以令T(x1)=Tρ(x)。这时,如果x1∉T1,可以重复步骤取x2,这些步骤是会终止的。因为T(xn)⊆T(xn-1)且1∈T1,所以存在一个xN满足xN∈T1。 如果存在只有一个φ-子集的S(x),那么存在一个数xN,满足xN∈T1。 (2) 假设xn和T(xn)由上述步骤得到,且T1(xn)是S(xn)不同与T(xn)的另一个φ-子集。 情形1 当T1(xn)∩T(xn-1)=∅时,对任意素数p∈P(xn-1),有 特别地,当p∈P(xn-1)-T(xn-1)时,因为T(xn)⊂T(xn-1),所以p∈P(xn)-T(xn)。 若p∈P(xn)-T1(xn),可得: vp(xn)+vp(xn-1)-vp(xn)=vp(xn-1)。 若p∈P(xn) ∩T1(xn),则 T1(xn)∩T(xn-1)=∅, 这与T1(xn)∩T(xn-1)=∅相矛盾。 这就证明了T1(xn)∪(T(xn-1)-T(xn))是S(xn-1)的不同于T(xn-1)的φ-子集。 情形2 当T1(xn)∩T(xn-1)≠∅时,有 T(xn-1)∩T1(xn)⊂ T(xn-1)∩S(xn)⊂ T(xn-1)∩Sρ(xn-1)=T(xn), 因此T1(xn)∩(T(xn-1)-T(xn))=∅。 同理可得,T1(xn)∪(T(xn-1)-T(xn))是S(xn-1)的不同于T(xn-1)的φ-子集。 由以上讨论可知,如果S(xn)存在一个不同于T(xn)的φ-子集T(xn-1),那么S(xn-1)也存在一个不同于T(xn-1)的φ-子集。 综合(1)、(2)可知,如果存在S(x)只有一个φ-子集,那么就一定存在一个数xN∈T1,使得S(xN)也只有一个φ-子集,即若猜想在集合T1成立,则猜想成立。即引理1得证。 定义2 P(x′)=P(x)且S(x′)⊂P(x′)}。 引理2 Carmichael猜想成立当且仅当猜想在T上集合成立。 证明若T(x)无法通过添加一个元素来生成新的φ-子集,则S(x′)⊂P(x)=P(x′)。 结合引理1,引理2得证。 证明因为对于任意x∈T,都有: 2∈S(x′)⊂P(x′)=P(x), 所以由定义2可得: 3∈S(x′)⊂P(x′)=P(x)。 以此类推,可得: 7∈S(x′)⊂P(x′)=P(x), 43∈S(x′)⊂P(x′)=P(x)。 于是有: {2,3,7,43}⊂P(x′)=P(x)。 故由x∈T可得,24337243|x。 由引理2,定理2得证。1 定理1的证明
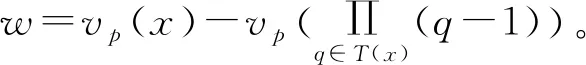
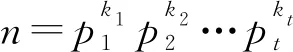
2 φ -子集的构造
2.1 添加一个元素到φ -子集生成新的φ -子集
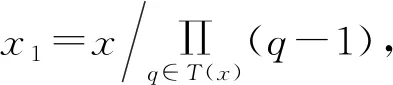
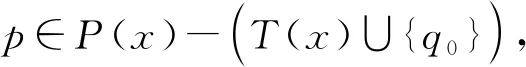
2.2 从φ -子集删除一个元素生成新的φ -子集
3 定理2的证明
3.1 相关引理的证明



3.2 定理2的证明

