窄基角钢输电塔结构力学性能研究
孙田鸽, 牛忠荣, 肖俊俊, 杨雪锋, 梁东跃
(1.合肥工业大学 土木与水利工程学院,安徽 合肥 230009; 2.安徽华电工程咨询设计有限公司,安徽 合肥 230022)
0 引 言
相关研究表明,输电铁塔在极限荷载工况下的结构性失稳,是引起倒塔事故的重要原因之一[1]。为了提高输电铁塔结构安全性与经济效益,需要对输电铁塔在各个荷载工况下的力学性能进行分析,并根据分析结果对输电铁塔进行优化,因此研究各个工况下输电铁塔的力学性能具有重要意义[2]。
目前,针对输电铁塔力学性能的研究成果较丰富。文献[3]对塔架的静力性能和动力性能都进行了研究,并考虑了杆件的初始缺陷、几何与材料非线性;文献[4]考虑了材料塑性和几何非线性,其极限荷载分析结果和真型试验结果的匹配度较高;文献[5]建立了输电铁塔的梁单元模型和梁-杆复合模型,分析了某输电铁塔的固有频率和振型,发现梁-杆复合模型更接近实际观测结果;文献[6]对输电铁塔塔架在各种荷载组合作用下的静力学与动力学行为进行了研究;文献[7]给出了窄基角钢塔在工程设计中重力二阶效应的计算方法,并根据有限元计算结果分析了重力二阶效应对窄基塔受力性能的影响。已有研究成果中对窄基塔的研究较少,且国内外针对窄基角钢塔并无成熟的技术规定可以参考,因此窄基角钢塔的受力性能及其破坏模式有待进一步的研究。
本文以一新型混压窄基角钢塔为研究对象,建立了角钢塔结构模型,采用有限元法进行了静力分析和屈曲分析,分别对正常使用荷载工况和大风极限荷载工况进行计算,并将有限元计算结果与该塔真型试验结果进行对比,由此给出该类窄基角钢塔在使用荷载工况下设计限值的建议值,可为该类杆塔的挠度值控制、强度评估、结构设计等提供参考。
1 窄基塔结构概况
某输电线工程中设计的一种110 kV混压窄基角钢塔,实现了110 kV线路在城区、城郊等路径拥挤地段与35 kV导线、10 kV导线同塔多回并廊走线。该输电塔高48.3 m,呼高27.0 m,根开3.012 m,高开比约为16.1。整个塔结构的质量为14.31 t。输电塔结构如图1所示。
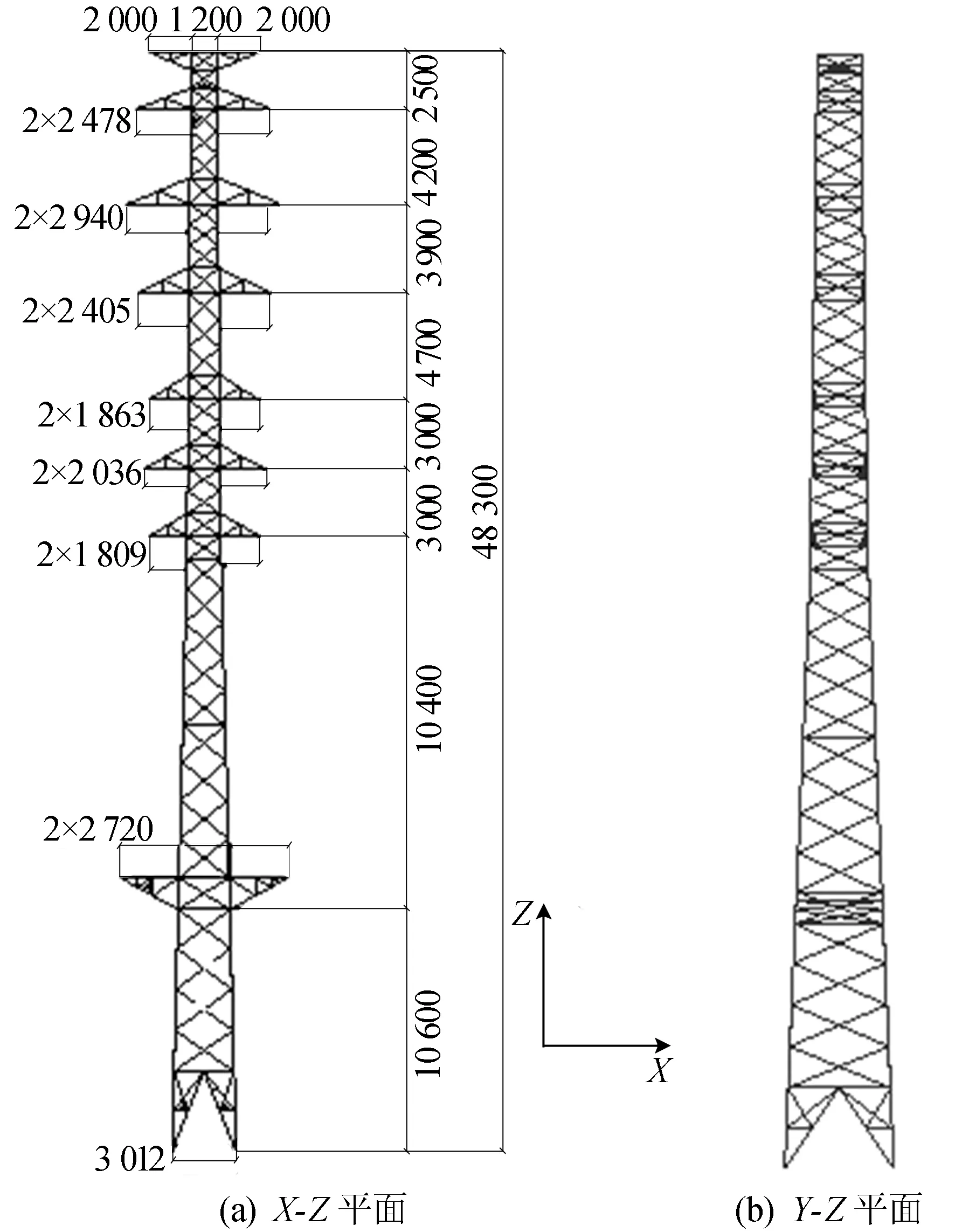
图1 输电塔结构
该输电塔设计环境和条件如下:处于平均海拔0~1 000 m处,最大风速为27 m/s,最大覆冰厚度为10 mm,110 kV导线采用1×JL/GIA-300/25钢芯铝绞线,35 kV导线采用1×JL/GIA-240/30钢芯铝绞线,10 kV导线采用JKLYJ-10 1×240钢芯铝绞线,地线为2根JLB20A-100铝包钢绞线,水平档距为220 m,垂直档距为260 m,最小垂直档距为187 m。
2 窄基塔结构力学分析
2.1 窄基塔结构模型
该窄基角钢塔所有杆件均为角钢,各个杆件之间通过连接板和螺栓连接。本文建立梁-杆单元混合模型进行有限元法力学分析,考虑到角钢的方向性,在有限元法分析中,输电塔主材选用两节点空间线性梁单元(BEAM31)进行建模,辅材和斜材采用两节点线性三维桁架单元(T3D2)进行建模,即主材与主材的连接视为刚接,主材与斜材的连接视为铰接,斜材与斜材之间无相互作用,对塔腿的4个节点进行全约束。结构有限元模型共划分梁单元152个、杆单元1 200个。输电塔的材料属性如下:主材采用Q420钢,斜材和辅材采用Q345钢和Q235钢。角钢的弹性模量为206 GPa,泊松比为0.3,密度为7 850 kg/m3。
荷载施加位置如图2所示。

图2 加载示意图
有限元分析选用以下2个代表工况:
工况1正常使用荷载工况。荷载组合为:长期荷载+平衡张力+90°风+最小转角+最大垂荷。
工况2 极限荷载工况。荷载组合为:大风+平衡张力+60°风+最小转角+最大垂荷。
由工况1分析结果可得到该窄基角钢塔在正常使用条件下的受力状态和变形情况,用以评估线路安全可靠的运行状况。
由工况2的分析结果可以得到该窄基角钢塔发生破坏时的荷载大小,可为该类塔型的设计限制提供参考。
塔顶位置左、右地线及风荷载的设计和试验荷载值见表1所列。

表1 2个工况下的设计与试验荷载 kN
注:风荷载大小为同一水平面4个节点荷载之和。
2.2 结构强度与刚度分析
为了得到该窄基角钢塔在各种荷载组合工况下的各种受力状态及变形情况,挑选输电塔主要传力构件如塔身、塔腿及横担主材处的部分杆件布置应力观测点,共计16处,测点布置如图3所示;采用全站仪进行位移测量,位移观测点的选择应能反映铁塔整体挠曲线,同时兼顾变形最大位置的观测,共计10处,如图4所示。
采用杆系有限元法对窄基角钢塔结构进行静力分析,得到2个工况下结构各个杆件的轴向应力值和结构在各个方向上的位移值。16个应力观测点的轴向应力值见表2所列,10个位移测点的位移计算结果见表3所列。

图3 应变测点布置 图4 位移测点布置
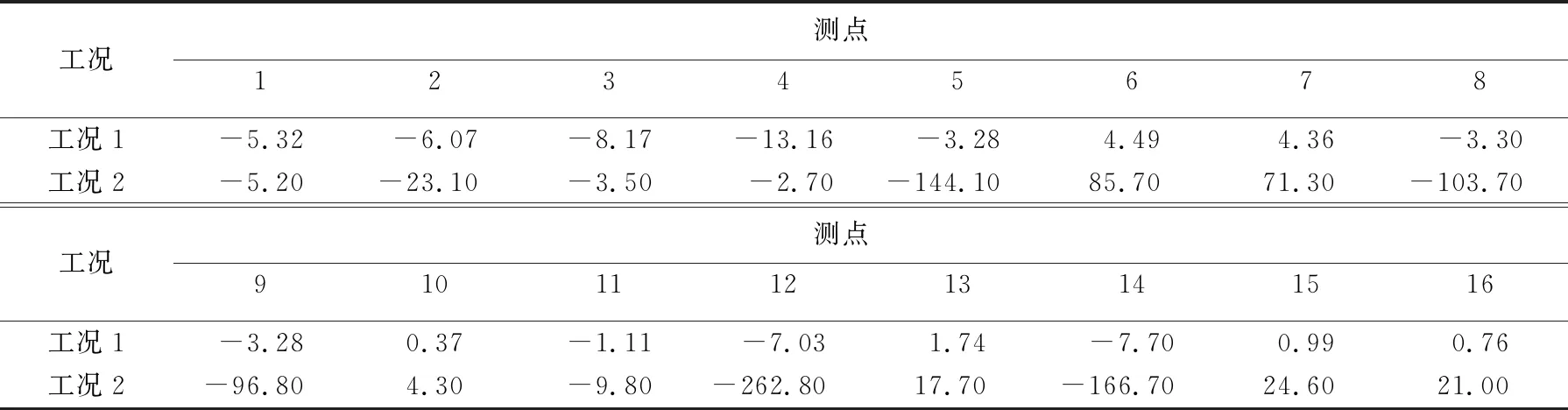
表2 角钢塔杆件轴向应力计算结果 MPa
注:负号表示压应力,下文同此。
由表2可知,工况1下,各杆件轴向应力值均不大,压应力最大值为13.16 MPa,出现在测点4第3横担东南侧靠近主材的横材处;工况2下,在输电塔塔腿最下端主材处2个测点(测点12和测点14)的轴向应力值较大,在测点12处压应力为262.80 MPa,在测点14处压应力为166.70 MPa。
由此可得出:在工况1下,由于考虑的风荷载较小,输电塔各主材轴向应力较小,且根据风荷载施加方向,迎风面上的主材为拉应力,背风处的主材为压应力,最大Mises应力值为13.16 MPa,发生在输电塔第3横担东南侧靠近主材的横材处,该处杆件采用Q345钢材,许用应力为310 MPa,最大Mises应力值远远小于许用应力值,结构安全;在工况2下,输电塔最大Mises应力值为262.80 MPa,出现在塔腿第1水平隔面上主材处,该处主材采用Q420钢材,许用应力为380 MPa,最大Mises应力值小于许用应力值的75%,结构安全。
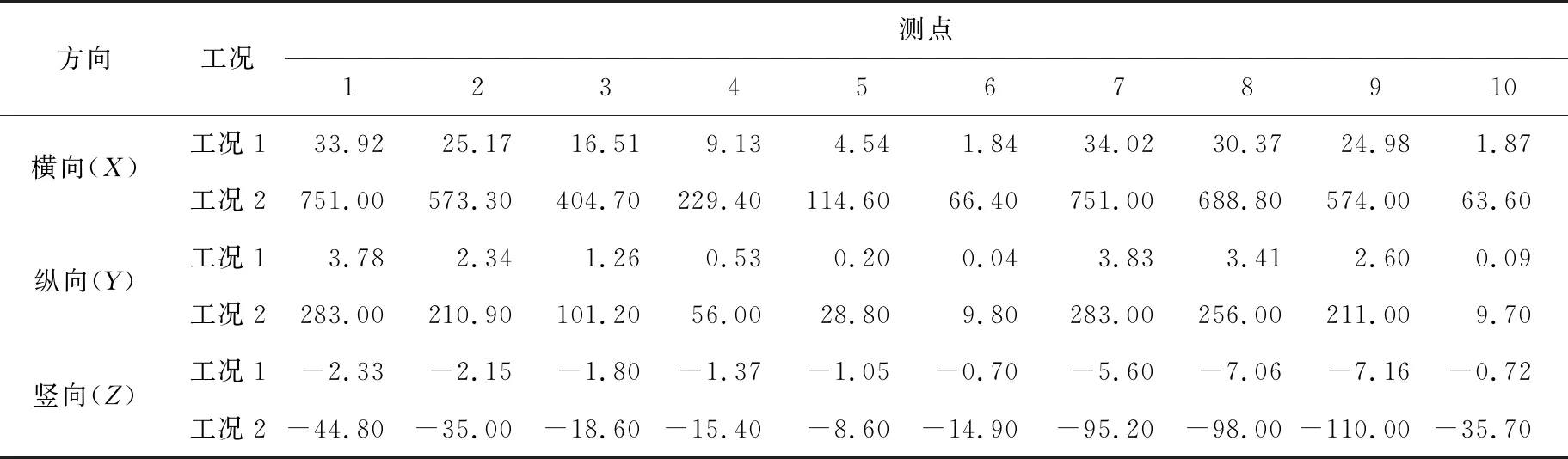
表3 角钢塔节点位移计算结果 mm
注:负号表示方向向下,下文同此。
由表3可知,工况1下,各位移测点在各个方向上的位移值较小,其中位移最大值出现在输电塔最高挂线处(测点7),X、Y、Z3个方向分别为34.02、3.83、-5.60 mm,组合位移为34.69 mm;工况2下,位移最大值也出现在测点7,X、Y、Z3个方向分别为751.00、283.00、-95.20 mm,组合位移为808.19 mm;测点10距地面18.0 m高的位置X、Y、Z3个方向位移分别为63.60、9.70、35.70 mm;在测点4距地面27.0 m高的位置X、Y、Z3个方向位移分别为229.40、56.00、15.40 mm;在测点9距地面41.6 m的位置X、Y、Z3个方向位移分别为574.13、211.00、110.03 mm。
由此可得出,输电塔在横向(X)和纵向(Y)的位移值随输电塔高度增加而增大,2个工况下水平方向位移均发生在输电塔最高挂线处。
2.3 结构屈曲分析
特征值屈曲分析又称线性屈曲分析,是用来分析理想结构的屈曲强度。其优点是在结构不需要进行非线性分析的情况下,就可以得到结构的临界载荷大小,可为非线性屈曲分析提供参考;缺点是在分析过程中没有考虑结构的初始缺陷和几何非线性因素的影响,其结果一般较为保守[8]。
通过计算分析得到输电塔在工况2下前8阶屈曲特征值见表4所列。
输电塔在工况2下第1阶和第5阶的屈曲变形如图5所示。

表4 窄基塔前8阶屈曲特征值
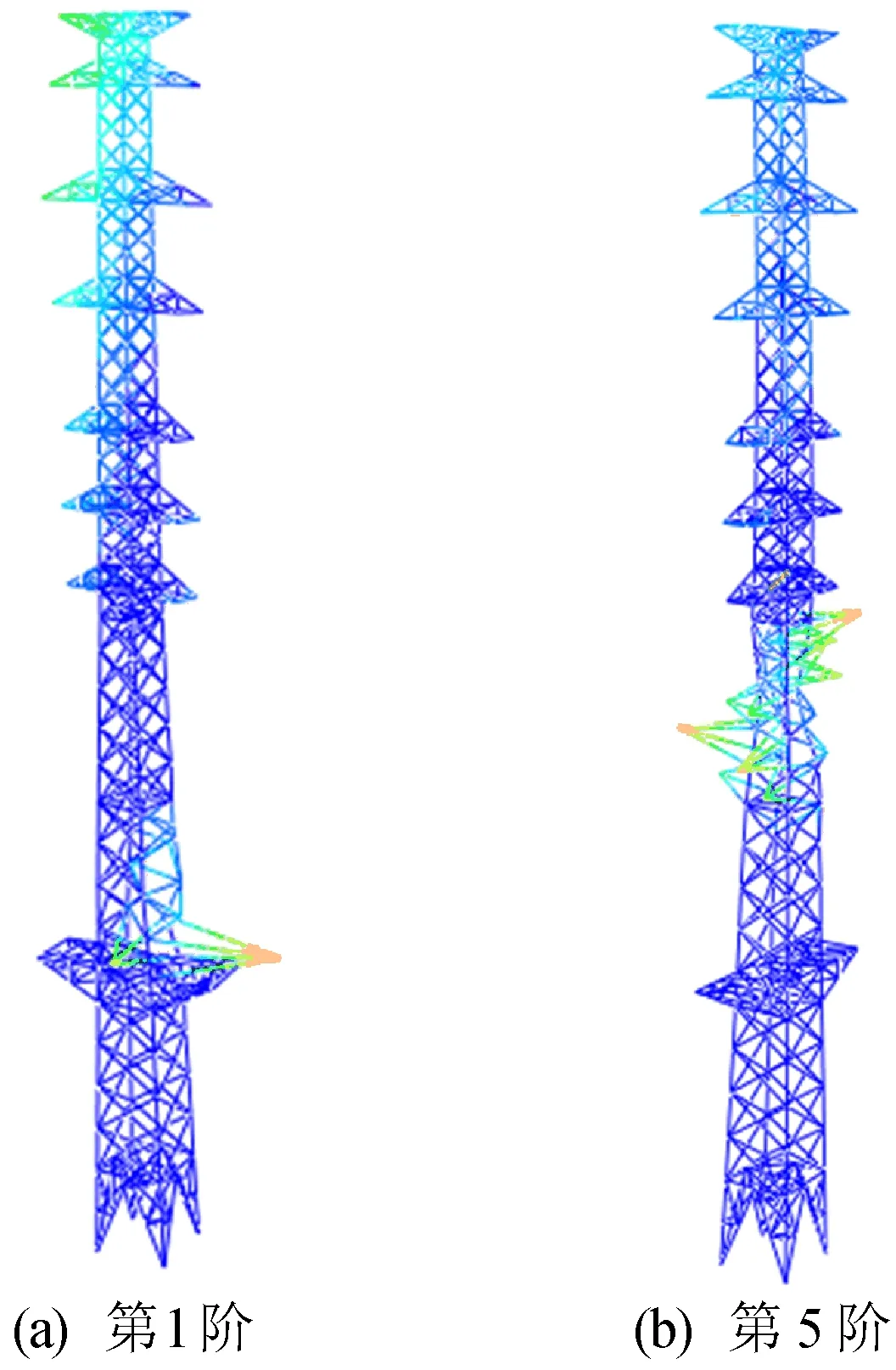
图5 屈曲变形图
由表4、图5可知,输电塔开始发生失稳的形式为第1段塔身辅材局部失稳,该阶段特征值的屈曲特征值为10.032,由此得知输电塔由稳定状态变为不稳定状态时的临界荷载为设计荷载的10.032倍;第5阶为辅材局部失稳,屈曲特征值为12.220,而输电塔结构依然没有发生屈曲破坏,由此可以得出此结构稳定性较好。
根据有限元计算结果,对铁搭东南角第1水平隔面上主材进行整体稳定性分析,稳定应力计算公式为:
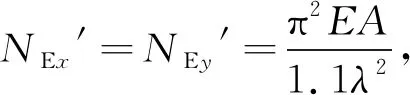
(1)
其中,下标x、y为杆截面惯性主轴;N为杆件工作轴力,计算值为1 270 kN;Mx为杆件在x轴上的弯矩,计算值为566.7 kN·mm;A为截面面积,A=5 547 mm2;φx为轴心受压构件稳定系数;βmx为x轴等效弯矩系数,βmx=1.0;W1x为在弯矩作用平面内对较大受压纤维的毛截面模量,W1x=131 400 mm3;γx为截面塑性发展系数,γx=1.05;E为弹性模量,E=206 GPa;λ为杆件长细比;l0x为构件计算长度,l0x=2.1l,l为杆件计算长度,l=1 801.328 mm;ix为截面回转半径,ix=54 mm;NEx、NEy′分别为杆件截面x、y轴欧拉临界压力,NEx′=NEy′=3 988.564kN;f为许用应力。
钢材材质为Q420钢,b类截面,根据文献[9],φx=0.561 8,f=380 MPa。将参数值带入(1)式计算可得:σ=412.51 MPa>380 MPa。
由分析结果可知,该处杆件稳定应力为412.51 MPa,超出了Q420钢材的许用应力380 MPa,该主材发生失稳。
3 窄基塔结构真型试验
3.1 静力试验
试验采用足尺寸真型结构,在试验场上对被试塔进行组装,加荷点通过连有测力传感器的钢丝绳和加荷用液压缸相连,加荷系统为液压闭环自动加荷系统。由于加荷塔部分加荷点的位置与其对应的试验塔的荷载位置不一致(可能出现水平偏移或高度差),为了保证试验塔各荷载作用点所受荷载与试验方案的要求相符,将各个工况的设计荷载值换算到对应的加荷钢丝绳所受荷载,称为试验荷载。换算过程如下:将每个水平截面上各个加载点的设计荷载相加,再分别通过左、右两端和中间3个加荷绳进行施加,同时要考虑加荷绳与设计加荷点之间的位置关系,即考虑其所成的角度。其中,该水平截面上所有横向荷载之和通过右端加荷绳施加,竖向荷载均匀分配到左、右两端的加荷绳进行施加,纵向荷载通过中间位置的加荷绳进行施加。试验荷载大小见表1所列,加载位置如图2所示。
通过静力试验可获得输电塔结构在静力荷载作用下的整体和局部响应,包括应变响应和位移响应[10]。
3.2 窄基塔静力试验结果
选择无风晴朗的天气对真型试验塔进行试验,通过加荷钢丝绳施加试验荷载于试验塔上,并约束试验塔4个塔脚处。通过静态应变数据采集仪得到各应变观测点的应变值并进行统计,通过全站仪观测得到各位移测点在各个方向上的位移值并进行统计。在工况2下,第1次加荷至设计荷载的100%时,测点1的横向位移为691 mm,纵向位移为177 mm,当荷载继续加至设计荷载的125%时,测点1的横向位移为950 mm,纵向位移为310 mm,此时试验塔没有发生倒塌。第2次加荷至设计荷载的130%时,测点1的横向位移为1 255 mm,竖向位移为207 mm,试验塔出现了较大的变形,当荷载持续时长约83 s后,输电铁塔东南腿第1水平隔面上主材弯曲破坏,随即导致整个输电塔结构的倒塌破坏。破坏情况如图6所示。

图6 真型试验破坏现场情形
工况2下各应变观测点的应变、应力值,见表5所列。应力计算公式为:
σ=Eε
(2)
其中,ε为应变实测值。
工况2下各位移测点在X、Y、Z方向上的位移结果见表6所列。
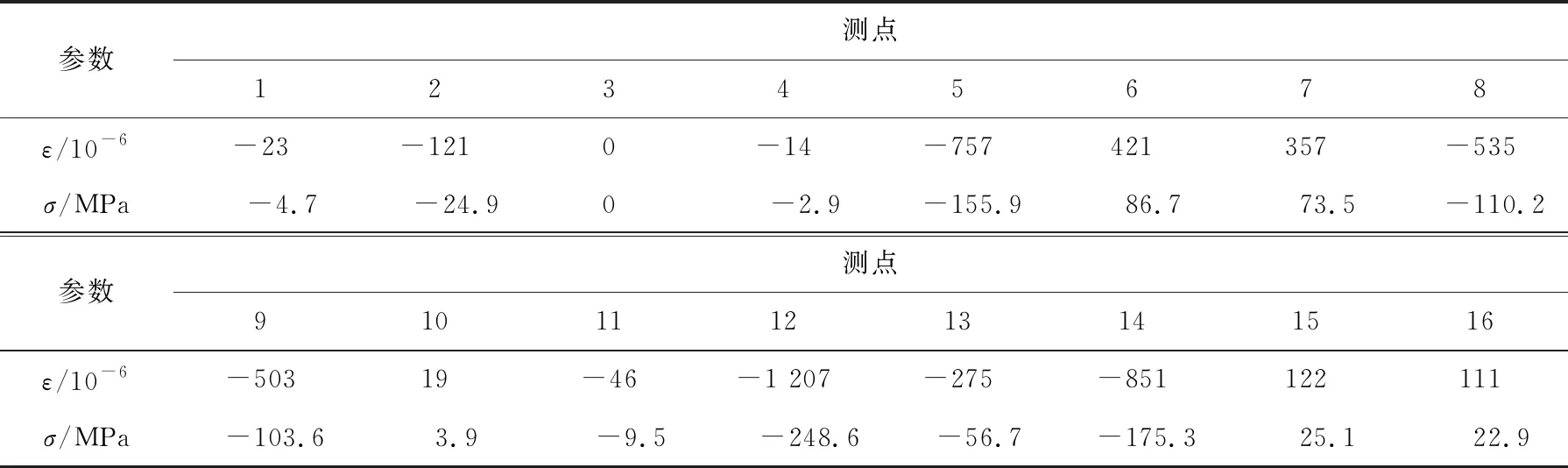
表5 工况2下窄基塔真型静力试验应力、应变结果

表6 工况2下窄基塔真型静力试验位移结果 mm
3.3 窄基塔试验结果与有限元法结果对比
3.3.1 窄基塔应力结果对比
将工况2下的应变实测值代入(2)式计算出轴向应力值,再与有限元法计算值进行对比,结果见表7所列。
通过对比发现,在工况2下,主要测点处的轴向应力计算值与试验值吻合较好,偏差均在10%以内,说明本文有限元法梁-杆计算模型的分析结果是可靠的。由于试验现场情况复杂,受天气和环境因素影响较多,个别杆件轴向应力值出现较大偏差,即测点13,试验值为56.70 MPa(压应力),计算值为17.70 MPa(拉应力)。测点13位于塔腿处连接主材和斜材的横腹杆,两端采用双螺栓连接,而有限元模拟简化为铰节点,可能是该测点应变片异常,或者数值模拟和试验的局部载荷有差异。测点3轴向应力计算值为3.50 MPa(压应力),而试验值为0 MPa,因应力小不作比较。

表7 工况2下窄基塔轴向应力试验值与有限元法计算结果对比 MPa
注:相对偏差=|计算值-试验值|/计算值。
3.3.2 窄基塔位移结果对比
将工况2下各位移测点在各个方向上的位移试验值与计算值进行对比,结果见表8所列。
从表8可以看出,在工况2下,沿主加载方向(横向)上的位移计算值与试验值整体相差不大,两者结果吻合较好。
由于试验现场情况复杂,受天气和环境因素影响较多,尤其是选择无风天气并不能保证完全无风的情况,且风荷载对位移值影响较大,然而数值模拟不能完全模拟现场的复杂情况,因此个别测点沿纵向(Y)方向位移值出现偏差,但是该方向垂直于加载方向,不是变形的主方向。其余测点在各个方向上的位移计算值与试验值偏差均在10%以内,在误差允许范围内。

表8 工况2下窄基塔位移试验值与有限元法计算结果对比 mm
注:相对偏差=|计算值-试验值|/计算值。
4 结 论
本文针对一新型110 kV混压窄基角钢塔建立了力学模型,采用有限元法对输电塔结构进行了静力分析和屈曲分析,并与真型试验结果进行对比,得出以下结论:
(1) 通过有限元计算结果与真型试验结果对比,可看出有限元计算结果与真型试验结果相差不大,由此可得出本文的窄基塔结构模型及有限元分析较为准确。
(2) 在正常使用荷载工况及极限荷载工况下,窄基角钢塔的强度限值以各杆件最大Mises应力值不超过其许用应力值的75%为依据。
(3) 根据有限元法分析结果,在正常使用荷载工况下,组合位移最大值为34.69 mm,小于3h/1 000(h为输电塔高度);在极限荷载工况下,组合位移最大值为808.18 mm,小于h/48。根据该塔型的真型结构试验结果,窄基塔在第1次加载125%的极限荷载组合时没有破坏,此时组合位移为1 001.96 mm,小于h/48;窄基塔在第2次加载130%的极限荷载组合时发生破坏,此时组合位移为1 274.66 mm。因此,在正常使用荷载工况下,窄基角钢塔的位移限值以不超过3h/1 000为依据,在极限荷载工况下,其位移限值以不超过h/48为依据。
(4) 为了验证铁塔的破坏机理,在有限元分析中对组合应力最大的杆件,即输电铁塔东南腿第1水平隔面上主材进行了整体稳定性分析,发现其稳定应力为412.51 MPa,超出Q420钢材的许用应力380 MPa,该主材发生失稳,与真型试验中铁塔发生弯曲破坏的杆件一致,由此可知,有限元计算结果是可靠的,其结果可为该类塔型的设计提供参考。

