考虑截止频率影响的输电塔线体系风振响应分析

陈佳昊, 黄文锋

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

电力是关系国计民生的基础产业,电力供应事关国家安全战略,事关经济社会发展全局。国家“十三五”规划对电力行业提出新的要求,而输电塔在输配电网中起着重要的作用。同一般建筑结构相比,窄基角钢塔不仅塔体高,而且具有跨度大、柔性高的特点,因此在风荷载的激励作用下,其动力响应十分敏感。

文献[1]提出谐波合成法(Weighted Amplitude Wave Superosition)模拟多维均匀高斯随机过程的脉动风荷载,但此方法在模拟多节点、长序列脉动风场时程时往往存在计算效率低、内存易超限的问题;文献[2]结合谐波合成法与本征正交分解技术提出了在保证计算精度的前提下,能大大提高计算效率的POD-谐波合成法;文献[3]提出了简化作用于输电塔体系的多变量三维脉动风场为多变量一维脉动风场的分析方法,应用谐波合成法和谱分解的适当修正,建立了脉动风速时程数值模拟方法;文献[4]采用谐波合成法生成脉动风速时程,并模拟生成了等效风雨荷载作用于塔线体系上,对结构进行了易损性分析。在计算风荷载、风雨荷载作用下的输电塔及塔线体系动力响应时,谐波合成法模拟风荷载有着广泛的应用。而在风荷载模拟过程中,脉动风的截止频率是一项重要参数,其不仅影响计算效率,对计算结果的准确性也有重要影响。以往研究对截止频率选取多采用经验值,因此有必要对截止频率的选取进行进一步的分析和探究。本文通过风振响应从脉动风能量和结构动力特性2个方面，对风荷载模拟所用截止频率的选取进行详细分析。

1 风荷载模拟

1.1 风荷载模拟理论

平均风速沿高度变化[5]可采用指数型风剖面,表达式为:

(1)

各国学者通过对良态风实测气象数据的分析提出了很多的风谱,如Davenport谱[6]、Simiu谱[7]和Kaimail谱[8]等。我国规范采用的是Davenport谱,表达式为:

(2)

(3)

其中,K为阻力系数;f为脉动频率。

顺风向脉动风v的统计特性可用互谱密度函数来描述,其表达式为:

(4)

其中,sij(n)、sjj(n)为自谱密度函数;φ(n)为相位角;相干函数coh(i,j,n)表达式为:

coh(i,j,n)=exp[-2f×

(5)

其中,Cx、Cy、Cz分别为空间任意2点左右、前后、上下的衰减系数;xi、xj、yi、yj、zi、zj分别为i和j点处x、y、z方向的坐标。

对于水平宽度很小的高耸式塔架可只考虑竖向的相关性,(5)式可简化为:

(6)

其中,Lz取60。

风工程界根据已知功率谱密度模拟平稳高斯随机过程的方法多采用精确度较高、稳定性较强的谐波合成法。谐波合成法是利用谱分解和三角级数叠加来实现随机过程样本的数值模拟。根据Shinozuka的理论,当N→∞时,各模拟点的风速时程模拟公式为[9]：

Vi(t)=

(7)

其中,N为频率等分数;θij(ωk)为结构上2个不同荷载点之间的相位角;φjk为介于0～2π之间均匀分布的独立相位角;Hij(ωk)为互谱函数密度矩阵进行Cholesky分解得到矩阵的第i行、第j列元素在ωk时的值;ωk为频率增量,该值计算公式为:

(8)

其中,ωμ为截止频率,采用以下标准估算[10]:

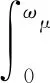
(9)

其中,e为精度参数;Sf0f0(ω)为自功率谱函数。

由(2)式、(8)式可得截止频率ωμ与e的关系如图1所示,0～4 Hz的脉动风能量占总体的90%,0～10 Hz的脉动风能量占总体的94%,因而工程中考虑脉动风作用时,多采用10 Hz以下的截止频率。但截止频率只有在30 Hz以后,脉动风总能量随截止频率的变化才趋于平缓,此时控制精度e达到2×10-2,而2 Hz以后的脉动风能量依然占到17%。

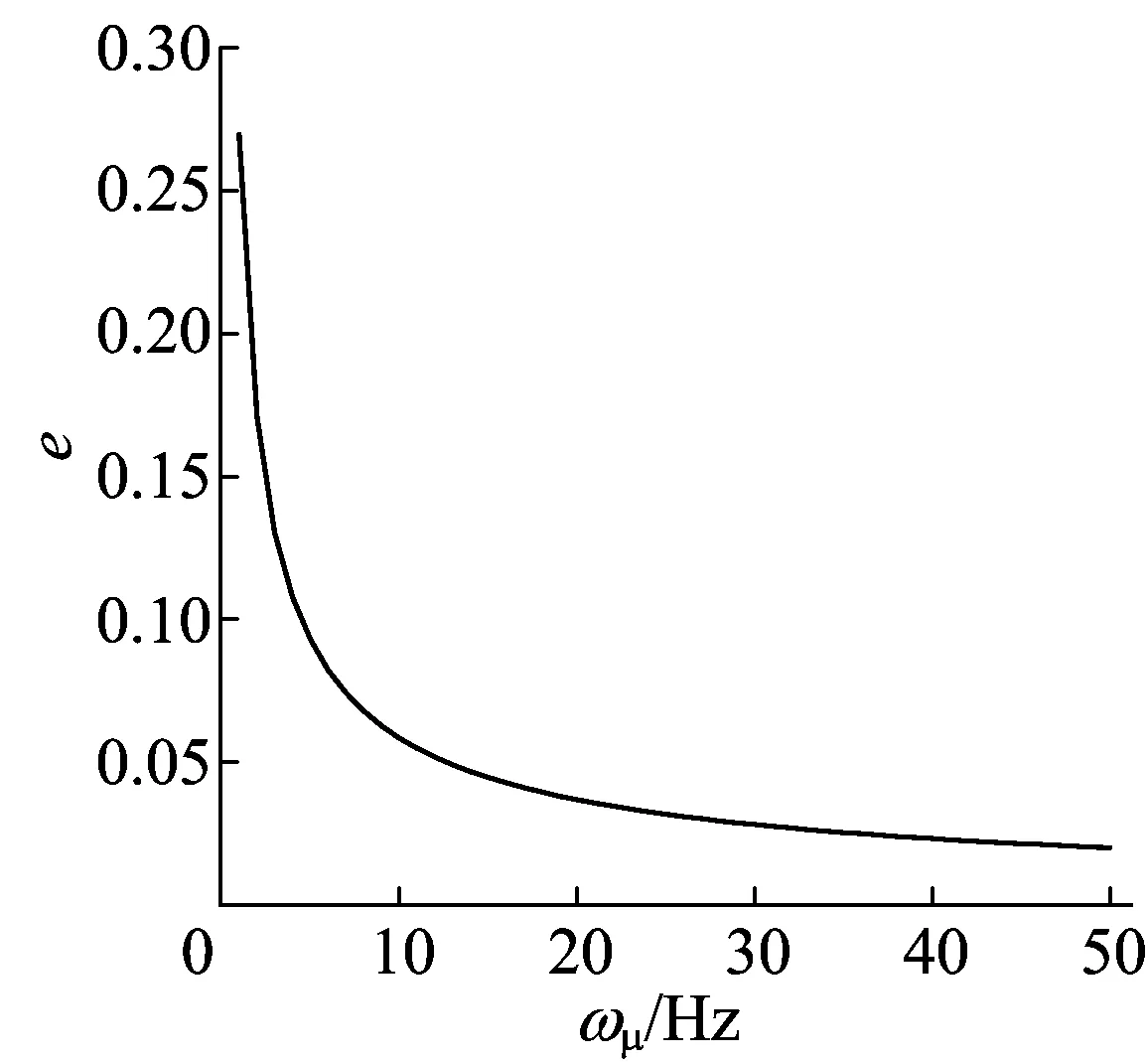
图1 精度参数

1.2 风场数值模拟

模拟风荷载的基本参数为:地面粗糙度取A类,10 m处基本风速取27 m/s,风速谱采用Davenport谱,阻力系数K表达式如下[11]:

(10)

数值模拟采用的截止频率分别取1 、2 、4 、8 、12 、16 Hz。由于篇幅限制,仅列出68 m高度处、截止频率为8 Hz时的脉动风速时程及模拟谱与目标谱的对比，如图2所示。

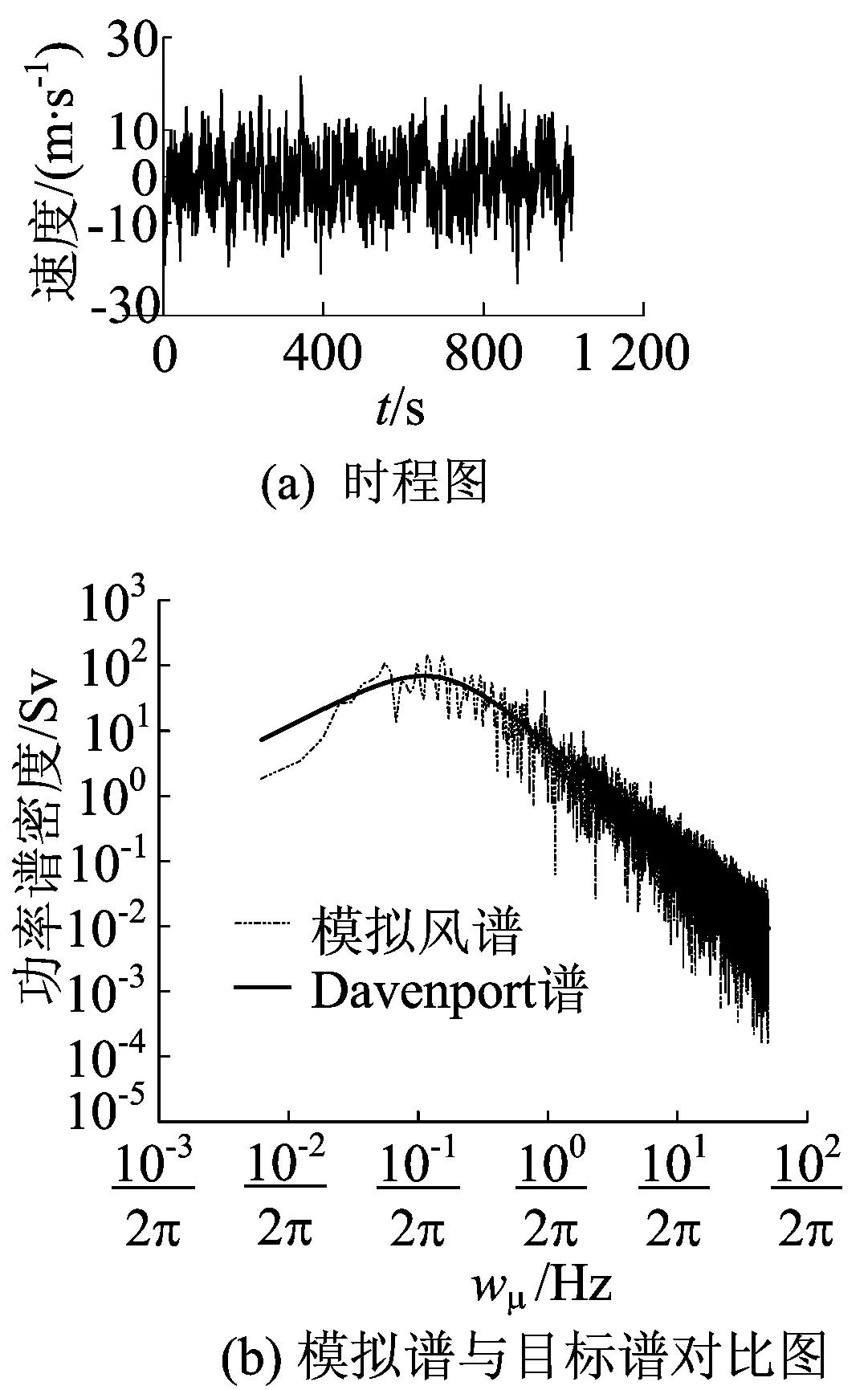
图2 风荷载模拟

由图2可知,模拟谱与目标谱总体趋势一致,说明模拟脉动风速模拟结果的有效性。

2 风振响应分析

2.1 有限元模型

本研究选用的输电塔为华东电网某混压输电线路窄基角钢塔,对3种单塔进行独立分析,塔高分别为38.2、46.4、68.4 m,各塔基本参数见表1所列。塔线体系选用三塔四线模型,该体系中输电塔取塔2,采用分裂式导地线,导线由绝缘子连接于输电塔横担,地线则直接连接在输电塔上,导地线两端使用铰结点约束,输电线参数见表2所列。输电塔采用桁-梁混合模型,主材及横隔材采用beam188单元,斜材及辅材采用link8单元,导地线和绝缘子采用link10单元。单塔及塔线模型如图3所示。

表1 窄基塔参数 m

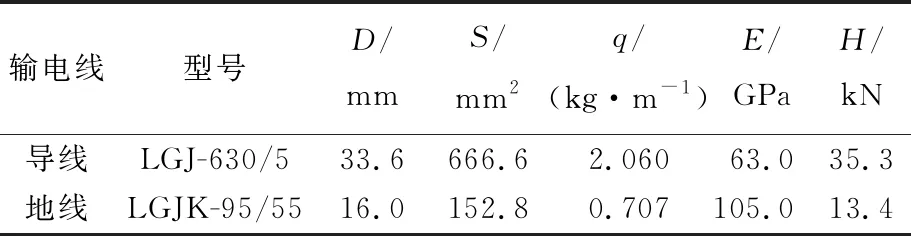
表2 输电线参数

图3 输电塔和塔线体系有限元模型

2.2 模态分析

通过控制边界条件,约束输电塔及两端输电线支座位移,采用求解收敛速度较快的Block Lanczos法进行模态分析,提取结构的固有频率并观察振型结果,单塔及塔线体系动力特性见表3、表4所列,其中,输电塔横向弯曲方向为垂直于横担方向。

由表3可知,塔1～塔3横向刚度依次递减,其中,塔1刚度最大,一阶频率达到2.29 Hz。由表4可知,塔线体系的自振频率十分密集,在低频处以导地线振动为主。受导地线影响,塔线体系中的输电塔在远低于单塔同阶振型的自振频率时就会发生平面外小幅振动,振幅逐渐增大,至单塔自振频率附近达到最大幅值,平面内未出现较早的耦合现象。发生这种现象的原因是,导地线增加了整体质量,同时对体系平面内刚度有所贡献,但对平面外的约束作用并不明显。

表3 输电塔动力特性

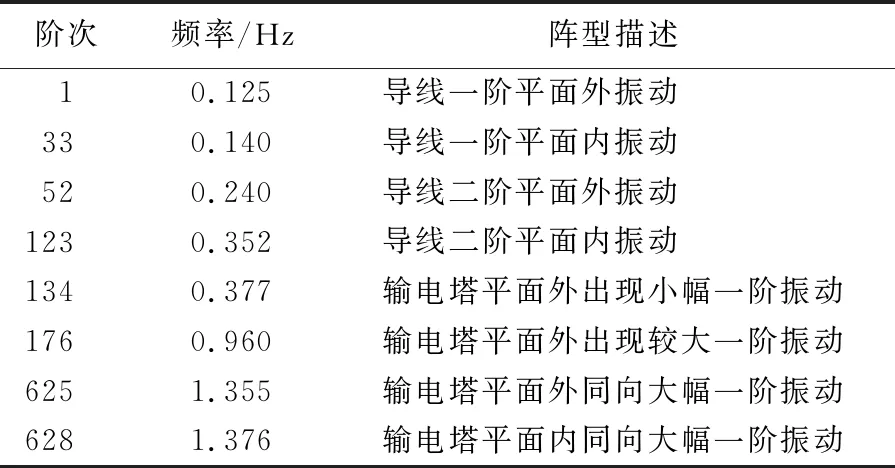
表4 输电塔线体系动力特性

2.3 动力响应分析

将模拟风荷载以集中力的形式分别作用于单塔和导地线上,运用ANSYS软件进行瞬态分析即可计算得到单塔及输电塔塔线体系的动力响应。受篇幅限制,仅列出塔顶端前100 s加速度时程，如图4所示。

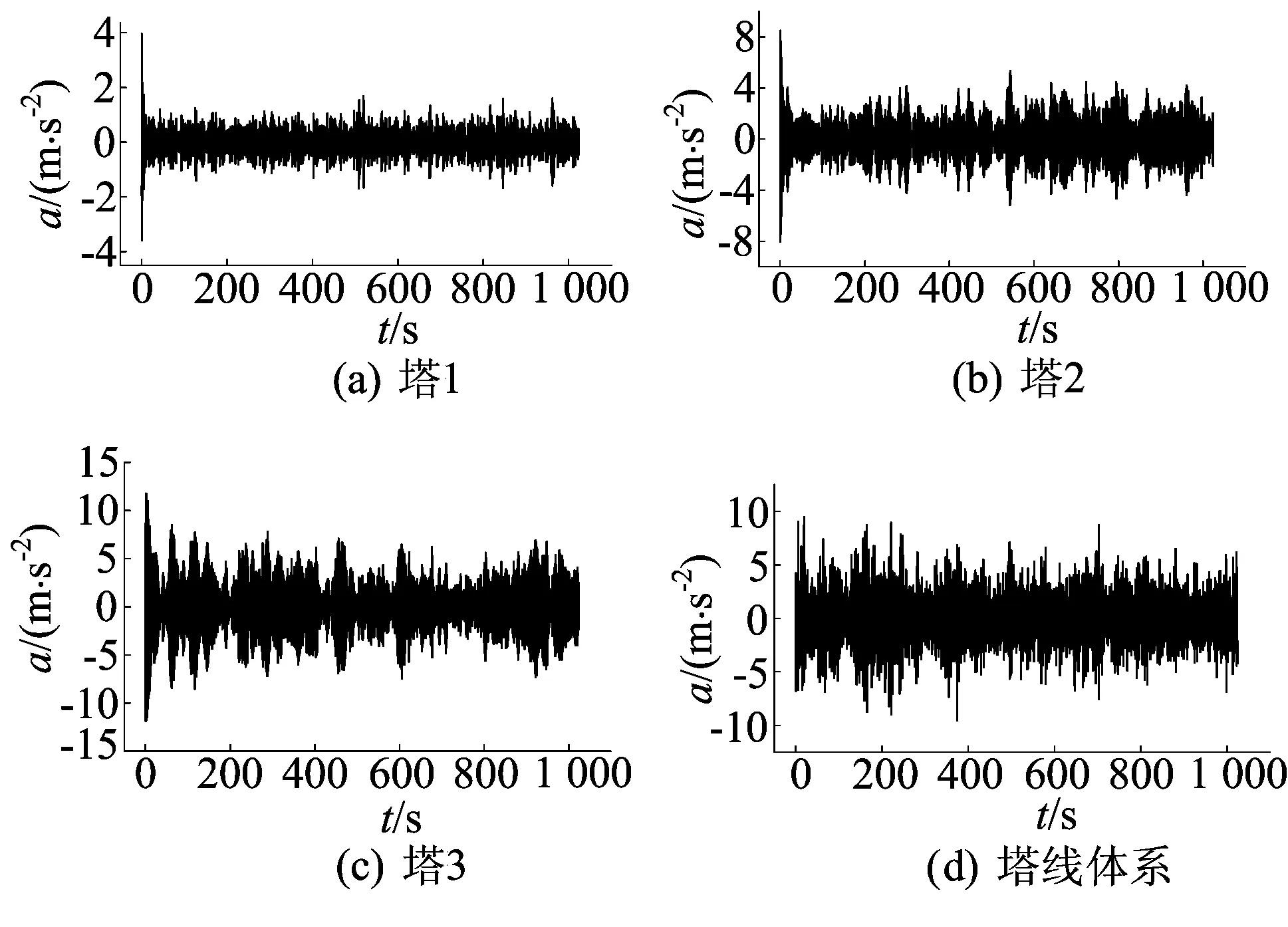
图4 加速度时程(ωμ=2 Hz)

各塔顶加速度响应均值为0,本文以加速度均方根值表示随机振动响应的强度,其比较结果如图5所示,输电塔及塔线体系的加速度响应见表5所列。

通过对3座输电塔在不同截止频率模拟风荷载作用下的塔顶端节点加速度均方根值的比较发现,在一定区间内,其加速度均方根值随着截止频率的增大而增大,随后增速有所放缓,直至增速接近为0。塔1～塔3分别在截止频率为4、8、16 Hz时,响应误差减小至10%以下。当选取小的截止频率时,对于刚度较大的输电塔而言,易造成较大误差,截止频率即使取到4 Hz,塔3响应误差依然达到25%,造成该结果的原因在于,脉动风在4 Hz以后的高频阶段仍有10%左右的风能,且对于刚度较大的输电塔而言,其易在高频段与风荷载发生共振现象。当选取较小截止频率时,此部分能量和风振响应被忽视；反之,受到导地线影响的塔线体系,对于低频段的风荷载较为敏感,高频段的风荷载对其影响不大,故而其加速度响应误差较单塔而言,相对较小。

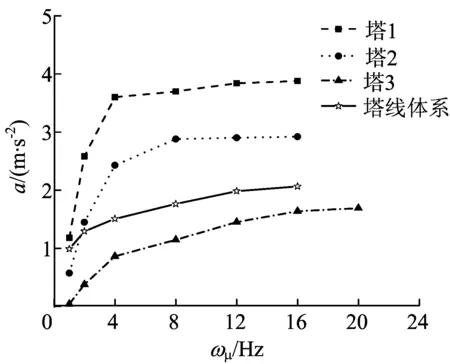
图5 加速度均方根值比较结果

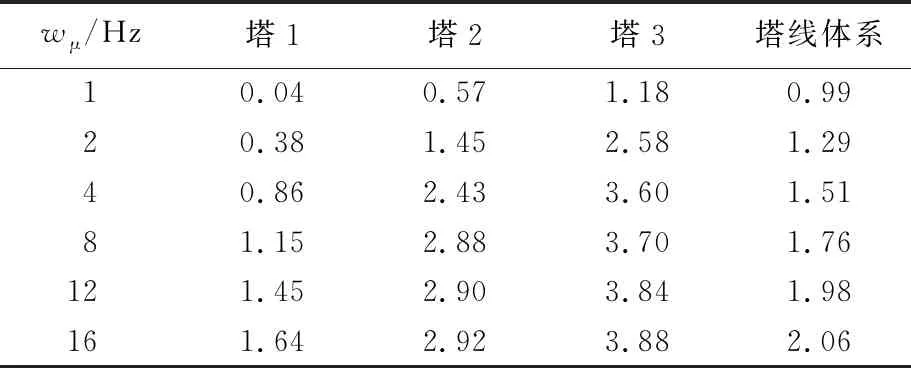
表5 输电塔及塔线体系的加速度响应m/s2

单塔及塔线体系在不同截止频率模拟的风荷载作用下,输电塔顶端节点的加速度功率谱如图6所示。

比较表3、图6可以发现,当风荷载截止频率在塔的固有一阶频率附近时,得到的响应谱峰值主要集中在塔一阶频率处,而当风截止频率超过二、三阶塔的固有频率时,塔响应谱受高频影响较大,峰值不仅仅在一阶出现,在二、三阶也相应出现。结合图5,进一步印证当风荷载截止频率增大时,输电塔在高频段与风荷载共振引起加速度响应的增大。

由图6d可知,塔线体系在横向风荷载作用时,加速度功率谱除了在单塔固有频率处出现峰值外,在低频处由于受到导地线的影响也出现相应峰值。

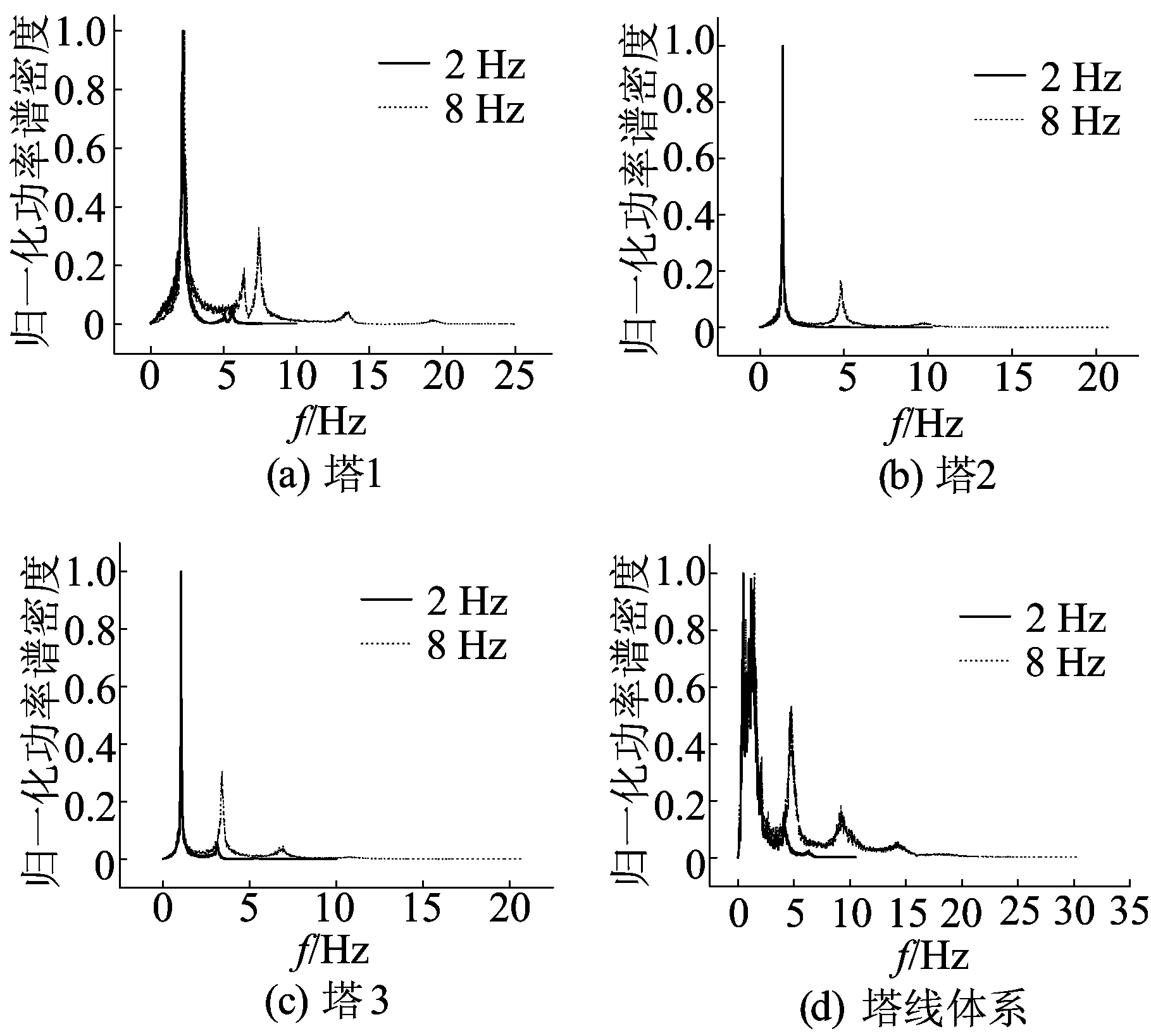
图6 加速度功率谱

3 结 论

本文采用风工程界广泛使用的谐波合成法模拟风荷载,通过模态分析获取结构自振特性,使用动力时程分析计算窄基角钢输电塔及塔线体系风振响应。将采用不同风荷载截止频率模拟得到的风荷载作用于输电塔及塔线体系进行结构响应计算,对风总能量、输电塔加速度均方根值以及加速度响应谱的计算结果进行对比分析发现,截止频率既要满足风谱总能量的要求,也要结合输电塔及塔线体系自身的动力特性进行选取。如果截止频率仅考虑风谱能量的要求,那么会忽视高频段的风荷载与输电塔共振的影响,部分刚度较大结构误差达到20%～30%,而当截止频率大于2～3阶结构固有频率时,误差会降至5%以下;而仅通过考虑结构自身动力特性影响选取截止频率,对刚度较小的结构会选用较小的截止频率,因风荷载在2 Hz以后的能量依然占到17%,会造成模拟风荷载能量的损失,进而影响结构响应计算精度。而采用过大的截止频率,为了满足精度要求,控制频带宽度,必须使用更多的采样点数,这样会造成计算量过大,降低计算效率。

随着国家电力行业的大力发展和超高压跨越输电塔的不断发展,风荷载对输电塔结构的影响不容忽视,使用最优截止频率模拟风荷载进行结构动力响应分析,不仅能准确计算结构动力响应,也能切实提高结构响应的计算效率。