广义仿拓扑群的若干性质研究*
1 引言
2014年,文[1]引进了广义拓扑群的概念并且研究了广义拓扑群的一些性质.2020年,文[2]推广了广义拓扑群的概念,引进了广义仿拓扑群的概念,并且对其性质做了研究,得到了每一个广义仿拓扑群是广义齐性空间,广义仿拓扑群的子群是广义仿拓扑群,广义仿拓扑群中的τ开子群是τ闭子群,广义仿拓扑群的商群是广义仿拓扑群,广义仿拓扑群到它的商群的自然映射是广义连续的广义开映射等结果.
本文继续研究广义仿拓扑群的性质,主要讨论了其广义邻域基、闭包运算、广义分离性质、同构、同态映射的广义连续性、广义乘积性、广义紧性等问题,获得了任意一个抽象群上的广义仿拓扑群化定理和广义仿拓扑群的一个广义拓扑同构定理,证明了每一广义仿拓扑群中单位元的广义开邻域生成的子群是广义开子群以及一族强广义仿拓扑群的广义乘积仍是广义仿拓扑群,并提出了一些问题.
2 预备知识
定义2.1([3])设X是非空集,X的幂集P(X)的子集族τ如果满足
(1)Ø∈τ;
(2)对任意i∈I,若Gi∈τ有∪i∈IGi∈τ,
则称τ是X上的广义拓扑,(X,τ)是广义拓扑空间,τ中的元为广义开集,每一广义开集的补集为广义闭集.X中所有广义开集组成的集族记为τ(X).
一个子集族B⊆τ称为广义拓扑空间(X,τ)的基([4]),如果τ中的每一元能表示成B中某些元素的并.
设(X,τ)是广义拓扑空间,x∈X.记τ(X,x)={U∈τ(X)∶x∈U}.
定义2.2([5])设(X,τ)是广义拓扑空间.称广义拓扑τ是强的,如果X∈τ.
定义2.3([3])设X和Y是广义拓扑空间,f∶X→Y是映射,则
(1)f称为广义连续的,如果对任意V∈τ(Y)有f-1(V)∈τ(X);
(2)f称为在x∈X处是广义连续的,如果对任意V∈τ(Y,f(x)),存在U∈τ(X,x)使得f(U)⊆V;
(3)f称为广义开(闭)的,如果X中每一广义开集(广义闭集)的像是Y的广义开集(广义闭集);
(4)f称为广义同胚,如果f是双射且f,f-1是广义连续的.
引理2.4([6])设(X1,τ1),(X2,τ2),…,(Xn,τn)是广义拓扑空间,X=X1×X2×…×Xn是乘积广义拓扑空间,则B={U1×U2×…×Un∶U1∈τ1,U2∈τ2,…,Un∈τn}是X的一个基.
定义2.5([3])设X是广义拓扑空间,B⊆X,x∈X.如果存在U∈τ(X)使得x∈U⊆B,则称B是x的广义邻域.
定义2.6([3])设X是广义拓扑空间,x∈X,B中的每一元是x的广义邻域.如果对任意U∈τ(X,x),存在B∈B使得B⊆U,则称B是x在X中的广义邻域基.
定义2.7([1,定义3.2])设(X,·)是群,(X,τ)是广义拓扑空间,定义映射
op2:X×X→X满足op2(x,y)=xy,∀x,y∈X;
Inv:X→X满足Inv(x)=x-1,∀x∈X.
如果op2和Inv是广义连续的,则称(X,·,τ)是广义拓扑群.
定义2.8([2,定义3.8])设(X,·)是群,(X,τ)是广义拓扑空间,定义映射
op2:X×X→X满足op2(x,y)=xy,∀x,y∈X.
如果op2是广义连续的,则称(X,·,τ)是广义仿拓扑群.
3 广义仿拓扑群的广义邻域基和闭包运算
首先,讨论广义仿拓扑群乘积的广义连续性问题:
定理3.1设X是广义仿拓扑群,定义映射opn:Xn→X满足opn(x1,x2,…,xn)=x1x2…xn,∀xi∈X,i=1,2,…,n,则opn是广义连续的.
证明由引理2.4,只需证:对任意xi∈X,i=1,2,…,n,若U∈τ(X,x1…xn),则存在U1∈τ(X,x1),U2∈τ(X,x2),…,Un∈τ(X,xn)使得U1U2…Un⊆U.
当n=1时,命题显然成立.
假设当n=k时命题成立.
设xi∈X,i=1,2,…,k+1,U∈τ(X,x1…xk+1).容易看到
x1…xk+1=op2((x1…xk,xk+1)).
由于X是广义仿拓扑群,op2是广义连续的且U∈τ(X,x1…xk+1),所以存在O∈τ(X×X,(x1…xk,xk+1))使得op2(O)⊆U.由引理2.4知,存在V∈τ(X,x1…xk),W∈τ(X,xk+1)使得(x1…xk,xk+1)∈V×W⊆O.从而
op2(V×W)⊆op2(O)⊆U,VW⊆U.
而V∈τ(X,x1…xk),所以由假设,存在U1∈τ(X,x1),U2∈τ(X,x2),…,Uk∈τ(X,xk)使得U1U2…Uk⊆V.
再令Uk+1=W,则
U1U2…Uk+1=(U1…Uk)W⊆VW⊆U.
故命题成立.
下面讨论广义仿拓扑群的广义邻域基.
引理3.2([2,定理3.13] )设X是广义仿拓扑群,a∈X,定义映射
ra:X→X满足ra(x)=xa,
la:X→X满足la(x)=ax,
则ra和la都是广义同胚.
定理3.3设X是广义仿拓扑群,U是X的子集族,x∈X,则以下条件等价:
(1) U是e的广义邻域基,
(2) {xU∶U∈U}是x的广义邻域基,
(3) {Ux∶U∈U}是x的广义邻域基.
证明设h∶X→Y是广义同胚,对任意x∈X,B是x的广义邻域基,则h(B)是h(x)的广义邻域基.
(1)→(2) 由于X是广义仿拓扑群,所以由引理3.2知映射lx∶X→X是广义同胚.若U是e的广义邻域基,则lx(U)={xU∶U∈U}是lx(e)=x的广义邻域基.
(2)→(1) 由于X是广义仿拓扑群,所以由引理3.2知映射lx-1∶X→X是广义同胚.若xU={xU∶U∈U}是x的广义邻域基,则lx-1(xU)=U是lx-1(x)=e的广义邻域基.
(1)→(3) 由于X是广义仿拓扑群,所以由引理3.2知映射rx∶X→X是广义同胚.若U是e的广义邻域基,则rx(U)={Ux∶U∈U}是rx(e)=x的广义邻域基.
(3)→(1) 由于X是广义仿拓扑群,所以由引理3.2知映射rx-1∶X→X是广义同胚.若{Ux∶U∈U}是x的广义邻域基,则U是e的广义邻域基.
引理3.4([2,推论3.18])设X是广义仿拓扑群,A,B⊆X,x∈X,则
(1) 如果A∈τ(X),则Ax,xA∈τ(X);
(2) 如果A∈τ(X),则AB,BA∈τ(X).
引理3.5设X是广义仿拓扑群,g,h∈X.定义映射
φ∶X→X满足φ(x)=gxh,∀x∈X,
则φ是广义同胚.
证明显然φ是双射.
设U∈τ(X),则φ-1(U)=g-1Uh-1.因为X是广义仿拓扑群,所以由引理3.4知φ-1(U)=g-1Uh-1∈τ(X),从而φ是广义连续的.
设V∈τ(X),则(φ-1)-1(V)=φ(V)=gVh.再由引理3.4,有(φ-1)-1(V)=gVh∈τ(X),从而φ-1是广义连续的.
故φ是广义同胚.
定理3.6设X是广义仿拓扑群,U是X中单位元e的广义邻域基,则有
(1) 对任意U∈U,存在V1,V2∈U使得V1V2⊆U;
(2) 对任意U∈U,g∈X,存在V∈U使得gVg-1⊆U.
证明(1) 设U∈U.由于X是广义仿拓扑群且op2(e,e)=e,所以存在Z∈τ(X×X,(e,e))使得op2(Z)⊆U,从而由引理2.4知存在O,W∈τ(X,e)使得(e,e)∈O×W⊆Z,于是
op2(O×W)⊆op2(Z)⊆U,即OW⊆U.
由于U是e的广义邻域基,所以取V1∈U使得V1⊆O,取V2∈U使得V2⊆W,则
V1V2⊆OW⊆U.
(2) 设U∈U,g∈X,定义映射
f∶X→X满足f(x)=gxg-1.
由引理3.5知f是广义同胚.因为U∈U,所以存在W∈τ(X,e)使得e∈W⊆U.取V∈U使得V⊆f-1(W),则由e∈f-1(W)且f-1(W)广义开于X有,
f(V)={gxg-1∶x∈V}=gVg-1⊆W⊆U.
定义3.7 ([7])设(X,τ)是广义拓扑空间,A⊆X.所有包含于A的广义开集的并称为A的广义内部,记作IntXA;所有包含A的广义闭集的交称为A的广义闭包,记作clXA.
定理3.8设(X,·)是群,U是X的子集族,单位元e∈∩U,满足:
(a) 对任意U∈U,存在V1,V2∈U使得V1V2⊆U;
(b) 对任意U∈U,g∈X,存在V∈U使得gVg-1⊆U,
则存在唯一的广义仿拓扑群(X,·,τ)使得U是(X,τ)中单位元e的广义邻域基.
证明分5步证明.(1)令τ={O⊆X∶对∀x∈O,∃U∈U使得xU⊆O},那么τ是X的广义拓扑.事实上,
(i) 显然,Ø∈τ;
(ii) 记τ={Oi}i∈∧.若z∈∪i∈∧′Oi,其中∧′⊆∧,则存在i0∈∧′使得z∈Oi0且存在U∈U使得zU⊆Oi0⊆∪i∈∧′Oi,从而∪i∈∧′Oi∈τ,故τ是X上的广义拓扑.
(2) 证明广义拓扑τ满足性质(*):若O∈τ且x∈X,则xO∈τ.
设g∈xO,则x-1g∈O.因为O∈τ,所以存在U∈U使得x-1gU⊆O,从而gU⊆xO,于是xO∈τ.
(3) 证明U是(X,τ)中e的广义邻域基.
(i) 证明单位元e的任意广义邻域包含U中某个元U.
设E是e的广义邻域,则e∈IntXE∈τ.由τ的定义知,存在U∈U使得
U=eU⊆IntXE⊆E.
(ii) 证明U中的每一元是e的广义邻域.
设U∈U.令W={x∈X∶∃V∈U使得xV⊆U},则e∈W⊆U.设x∈W,则存在V∈U使得xV⊆U.由(a)知,存在P1,P2∈U使得P1P2⊆V.因为对任意y∈xP1有
yP2⊆xP1P2⊆xV⊆U,
所以y∈W,从而xP1⊆W,因此W∈τ,故U是e的广义邻域.
这样,U是e广义邻域基.
(4) 证明(X,·,τ)是广义仿拓扑群.
设W*∈τ,x,y∈X满足xy∈W*.由τ的定义知,存在A∈U使得xyA⊆W*.由(a)知,存在U1,U2∈U使得U1U2⊆A,从而xyU1U2⊆xyA⊆W*.由(b)知,存在V⊆U使得y-1Vy⊆U1,从而V⊆yU1y-1,于是xVyU2⊆xyU1y-1yU2=xyU1U2⊆W*.因为V,U2是e的广义邻域,故由性质(*)知xV是x的广义邻域,yU2是y的广义邻域,从而映射op2∶X×X→X是广义连续的.
(5) 证明唯一性.
设(X,·,σ)是广义仿拓扑群使得U是e在(X,σ)上的广义邻域基.下证τ=σ.
设U∈τ,则对任意x∈U,由引理3.4,有e∈Ux-1∈τ,于是存在A∈U使得e∈A⊆Ux-1.取O∈σ使得e∈O⊆A,则x∈Ox⊆Ax⊆U.再由引理3.4可知,Ox∈σ.所以U∈σ.于是τ⊆σ.
同理σ⊆τ.故τ=σ.
下面讨论广义仿拓扑群的闭包和内部运算.
引理3.9设X,Y是广义拓扑空间,f∶X→Y是广义同胚映射,A⊆X,则
(1) clY(f(A))=f(clXA),
(2) IntY(f(A))=f(IntXA).
证明(1) 因为f是广义同胚,所以f(clXA)=clY(f(clXA)),从而
clY(f(A))⊆clY(f(clXA))=f(clXA).
反之,由于f(A)⊆clY(f(A)),所以A⊆f-1(clY(f(A))).因为clY(f(A))是Y中的广义闭集,f是广义同胚,所以f-1(clY(f(A)))是X中广义闭集,从而clXA⊆f-1(clY(f(A))),因此f(clXA)⊆clY(f(A)).
故clY(f(A))=f(clXA).
(2) 设y∈IntY(f(A)),则f(A)是y的广义邻域,所以存在Y的广义开集U使得y∈U⊆f(A),从而存在x∈f-1(y)⊆f-1(U)⊆A.由于f是广义同胚,所以A是x的广义邻域,从而x∈IntXA,于是y=f(x)∈f(IntXA),因此IntY(f(A))⊆f(IntXA).
反之,由于f是广义同胚,所以f(IntXA)=IntY(f(IntXA)),从而
f(IntXA)=IntYf(IntXA)⊆IntY(f(A)).
故IntY(f(A))=f(IntXA).
定理3.10设X是广义仿拓扑群,A⊆X,g,h∈X,则
clX(gAh)=g(clXA)h,g(IntXA)h=IntX(gAh).
证明定义映射
f∶X→X满足f(x)=gxh,∀x∈X.
由引理3.5知f是广义同胚,所以由引理3.9知
clX(gAh)=clX(f(A))=f(clXA)=g(clXA)h,
IntX(gAh)=IntX(f(A))=f(IntXA)=g(IntXA)h.
引理3.11设X是广义拓扑空间,A⊆X,则x∈clXA当且仅当对x的任意广义邻域U有U∩A≠Ø.


定理3.12设X是广义拓扑群,A⊆X,U是X中单位元e的广义邻域基,则
clXA=∩U∈UUA=∩U∈UAU.
证明先证clXA⊆∩U∈UUA和clXA⊆∩U∈UAU.
设x∈clXA,U∈U.由定理3.3知{xU∶U∈U}和{Ux∶U∈U}是x的广义邻域基.又X是广义拓扑群,存在V∈U使得V-1⊆U.由引理3.11,有
(xV)∩A≠Ø且(Vx)∩A≠Ø,
于是存在v,w∈V使得xv∈A且wx∈A,所以
x=(xv)v-1∈AV-1⊆AU且x=w-1(wx)∈V-1A⊆UA,
因此clXA⊆UA且clXA⊆AU,从而
clXA⊆∩U∈UUA和clXA⊆∩U∈UAU.
再证∩U∈UUA⊆clXA.
若上式不成立,则存在x∈∩U∈UUAclXA.由定理3.3及引理3.11知,存在U∈U使得Ux∩A=Ø.取V∈U使得V-1⊆U,则由假设知x∈VA,所以存在v∈V,a∈A使得x=va,从而a=v-1x∈V-1x⊆Ux,矛盾.故∩U∈UUA⊆clXA.
下证∩U∈UAU⊆clXA.
若上式不成立,则存在x∈∩U∈UAUclXA.由定理3.3及引理3.11知,存在U∈U使得xU∩A=Ø.取W∈U使得W-1⊆U,则由假设知x∈AW,所以存在w∈W,a∈A使得x=aw,从而a=xw-1∈xW-1⊆xU,矛盾.故∩U∈UAU⊆clXA.
问题3.13定理3.12对广义仿拓扑群成立吗?
4 广义仿拓扑群的广义分离性质
定义4.1([8,定义2.1])设(X,τ)是一个广义拓扑空间,(X,τ)称为广义T1空间,如果对任意x,y∈X,x≠y,存在x的广义开邻域U使得y∉U且存在y的广义开邻域V使得x∉V.
引理4.2([8,定理3.2])设(X,τ)是一个广义拓扑空间,则以下条件等价:
(1)X是一个广义T1空间,
(2)X中每个单点集都是广义闭集,
(3)X的每个有限子集都是广义闭集.
定理4.3设X是广义仿拓扑群,e是X的单位元,则X是广义T1空间当且仅当{e}广义闭于X.


clX({x})=clX(x{e})=xclX({e})=x{e}={x},
于是所有单点集{x}是广义闭集,因此由引理4.2知X是广义T1空间.
定理4.4设X是广义拓扑群,U是单位元e的广义邻域基,U∈U,则clXU⊆U2.
证明由定理3.12知,对任意A⊆X有
clXA⊆∩V∈UVA⊆UA.
取A=U,则clXU⊆U2.
问题4.5定理4.4对广义仿拓扑群成立吗?
定义4.6([8,定义2.2])设(X,τ)是一个广义拓扑空间.(X,τ)称为广义正则空间,如果对任意x∈X,F广义闭于X且x∉F,存在x的广义开邻域U,F的广义开邻域V使得U∩V=Ø.
定义4.7([8,定义2.1])设(X,τ)是一个广义拓扑空间,(X,τ)称为广义T2空间,如果对任意x,y∈X,x≠y,存在x的广义开邻域U,y的广义开邻域V使得U∩V=Ø.
引理4.8([8,定理2.3])广义正则的广义T1空间是广义T2空间.
引理4.9设X是一个广义拓扑空间,则X是一个广义正则空间当且仅当对任意x∈X,x的任意广义开邻域U,存在x的广义开邻域V使得clXV⊆U.


定理4.10 每个广义拓扑群是广义正则的.
证明设X是广义拓扑群,e是X中的单位元,U是e的广义邻域基.现设O是x的广义开邻域,则x-1O是e的广义开邻域.由定理3.6知存在V1,V2∈U使得V1V2⊆x-1O,而由定理3.12知clXV2⊆V1V2⊆x-1O,从而x∈xV2⊆clX(xV2)=x(clXV2)⊆O.最后,由引理4.9知X是广义正则的.
由引理4.8和定理4.10可直接得到
定理4.11每个广义T1的广义拓扑群是广义T2的.
问题4.12定理4.10对广义仿拓扑群成立吗?
5 广义仿拓扑群的子群
引理5.1设X是一个广义拓扑空间,A,B⊆X,则clXA×clXB=clX×X(A×B).
证明设(x,y)∈clXA×clXB,R是(x,y)的任意广义邻域.由引理2.4知存在广义开集O,W使得(x,y)∈O×W⊆R.由引理3.11,得O∩A≠Ø且W∩B≠Ø,从而
R∩(A×B)⊇(O×W)∩(A×B)=(O∩A)×(W∩B)≠Ø.
故,clXA×clXB⊆clX×X(A×B).
反之,设(x,y)∈clX×X(A×B).令U是x的任意广义邻域,V是y的任意广义邻域.由引理2.4知U×V是(x,y)的广义邻域.所以由引理3.11,得
(U∩A)×(V∩B)=(U×V)∩(A×B)≠Ø,
因此,x∈clXA,y∈clXB,clXA×clXB⊇clX×X(A×B).
故clXA×clXB=clX×X(A×B).
引理5.2设X,Y是广义拓扑空间,f∶X→Y是广义连续的,A⊆X,则
f(clXA)⊆clY(f(A)).
证明设A⊆X.因为f是广义连续的,所以f-1(clY(f(A)))是广义闭集且
f-1(f(A))⊆f-1(clY(f(A))).
由广义闭包的概念知
clX(f-1(f(A)))⊆f-1(clY(f(A))),
从而
clXA⊆clX(f-1(f(A)))⊆f-1(clY(f(A))).
因此
f(clXA)⊆clY(f(A)).
定理5.3设X是广义拓扑群.若H是X的子群,则clXH是X的子群.
证明先证:对任意A,B⊆X有(clXA)(clXB)⊆clX(AB).
由于op2是广义连续的,所以由引理5.2知
op2(clX×X(A×B))⊆clX(op2(A×B))=clX(AB),
从而由引理5.1,有
(clXA)(clXB)=op2(clXA×clXB)=op2(clX×X(A×B))⊆clX(AB).
注意到HH=H且H-1=H,所以由上面所得知
(clXH)(clXH)⊆clX(HH)=clXH.
由引理3.9有(clXH)-1=clX(H-1)=clXH.故clXH是X的子群.
例5.4([9,例子1.4.17])存在仿拓扑群X(进而是广义仿拓扑群)的子群H使得clXH不是X的子群.
定理5.5设X是广义仿拓扑群,H是X的子群.若IntXH≠Ø,则H广义开于X.
证明设O=IntXH.由引理3.4知HO广义开于X.因为O⊆H,所以HO⊆HH=H.取k∈O,则
H={(hk-1)k∶h∈H}⊆HO,
所以H=HO,从而H广义开于X.
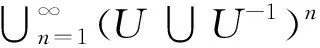

定义5.7设X是一个广义仿拓扑群,H是X的子群,称H在X中广义局部闭,如果存在h∈H及存在h在X中的某一广义邻域U使得U∩H在子空间U中广义闭.
问题5.8设X是一个广义仿拓扑群,H是X的子群.如果H在X中广义局部闭,那么H是否在X中广义闭?
6 广义仿拓扑群的商群
本节将在文[2]的基础上继续探讨广义仿拓扑群的商群.
引理6.1([2,定理3.26])设X是广义仿拓扑群,H≤X.如果X/H为X的关于H的广义陪集空间,则自然广义商映射η∶X→X/H是广义连续的广义开映射.
定理6.2设X是广义仿拓扑群,H是X的正规子群,则X/H是广义T1的当且仅当H是广义闭的.


设X,Y是群,f∶X→Y是群同态,定义映射
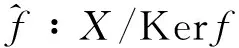
φKerf∶X→X/Kerf,满足φKerf(x)=xKerf,x∈X,

定理6.3设X,Y是广义仿拓扑群,f∶X→Y是群同态,则有
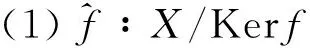
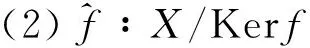



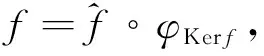
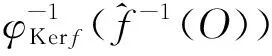
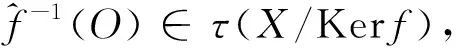


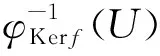
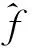
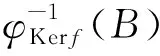
定义6.4设(X,·,τ)和(Y,∘,π)是广义仿拓扑群.称映射f∶X→Y是(X,·,τ)和(Y,∘,π)之间的广义拓扑同构,如果f既是广义拓扑空间(X,τ)和(Y,π)之间的广义同胚,也是群(X,·)和(Y,∘)之间的同构.
广义仿拓扑群(X,·,τ)和(Y,∘,π)是广义拓扑同构的,如果它们之中存在一个广义拓扑同构.
由定理6.3可以直接得到
定理6.5设X,Y是广义仿拓扑群,f∶X→Y是满的广义连续的广义开同态,则Y和X/Kerf广义拓扑同构.
7 广义仿拓扑群的同态映射
下面的引理是显然的.
引理7.1设X,Y是广义拓扑空间,f∶X→Y是双射,则f是广义开的当且仅当f是广义闭的.
定理7.2广义仿拓扑群之间的广义闭的满同态是广义开的.

定理7.3设X,Y是广义仿拓扑群,f∶X→Y是同态,则f在X中某一点是广义连续的当且仅当f是广义连续的.

设p∈X,V是f(p)在Y中的广义邻域,则存在广义开集W广义开于Y,使得f(p)∈W⊆V.从而
f(x0)=f(x0)f(p)-1f(p)∈f(x0)f(p)-1W⊆f(x0)f(p)-1V.
由引理3.4知f(x0)f(p)-1V是f(x0)在Y中的广义邻域.因为f在x0∈X上是广义连续的,所以f-1(f(x0)f(p)-1V)是x0在X中的广义邻域,从而px0-1f-1(f(x0)f(p)-1V)是p在X中的广义邻域.又f是同态,所以
x∈f-1(f(x0)f(p)-1V)⟺f(x)∈f(x0)f(p)-1V⟺f(p)f(x0)-1f(x)∈V⟺
f(p)f(x0-1)f(x)∈V⟺f(px0-1x)∈V⟺px0-1x∈f-1(V)⟺x∈x0p-1f-1(V).
从而f-1(f(x0)f(p)-1V)=x0p-1f-1(V).进而f-1(V)是p在X中的广义邻域,于是f是广义连续的.

定义7.4设X,Y是广义拓扑空间,f∶X→Y,x∈X.如果对x的每一广义邻域U,f(U)是f(x)在Y中的广义邻域,则称f在点x上是广义开的.
引理7.5设X,Y是广义拓扑空间,则f∶X→Y是广义开映射当且仅当f在X中每一点上是广义开映射.


定理7.6设X,Y是广义仿拓扑群,f∶X→Y是同态.如果f在X中某一点上是广义开的,则f是广义开的.
证明设f在x0∈X上是广义开的,下证f在X中每一点上都是广义开的.
设p∈X,W是p在X中的广义邻域,则存在广义开集O广义开于X,使得p∈O⊆W,所以x0=x0p-1p∈x0p-1O⊆x0p-1W.由引理3.4知x0p-1W是x0在X中的广义邻域,所以f(x0p-1W)是f(x0)在Y中的广义邻域,从而存在广义开集Q广义开于Y,使得f(x0)∈Q⊆f(x0p-1W)=f(x0)f(p-1)f(W).于是
f(p)∈f(p)f(x0)-1Q⊆f(W).
再由引理3.4知f(W)是f(p)在Y中的广义邻域,从而由引理7.5,f是广义开的.
8 广义仿拓扑群的广义乘积
定义8.1([10])设(Xα,·)是群,α∈A,定义集合∏α∈AXα上的运算·,满足(xα)α∈A·(yα)α∈A=(xα·yα)α∈A,则称(∏α∈AXα,·)是群(Xα,·)的乘积群.
定义8.2([6])设(Xα,τα)是广义拓扑空间,α∈A,记
B={∏α∈AMα∶Mα∈τα,且除有限个α外Mα=∪τα}.
称B是X=∏α∈AXα上某一广义拓扑τ的基,τ是广义拓扑τα的乘积.
定理8.3设{(Xα,·,τα)∶α∈A}是广义仿拓扑群构成的集族,且子集Yα=∪τα(⊆Xα)上的二元运算封闭,即∀x,y∈Yα,有x·y∈Yα,α∈A,则乘积X=∏α∈AXα是广义仿拓扑群.特别地,一族强广义仿拓扑群的广义乘积仍是广义仿拓扑群.
证明设x,y∈X,令z=xy.记x=(xα)α∈A,y=(yα)α∈A,z=(zα)α∈A,其中对任意α∈A有zα=xαyα.
设O是z在X中的广义邻域,则存在Wα广义开于Xα使得z∈W=∏α∈AWα⊆O,其中除了有限个α1,…,αm,其余Wα=∪τα.因为Xαk(1≤k≤m)是广义仿拓扑群且xαkyαk=zαk,所以存在(xαk,yαk)的广义邻域zαk使得op2(Zαk)⊆Wαk.由引理2.4知,存在xαk的广义开邻域Uαk,yαk的广义开邻域Vαk使得Uαk×Vαk⊆Zαk,从而
UαkVαk=op2(Uαk×Vαk)⊆op2(Zαk)⊆Wαk.
对任意α∈A{α1,…,αm},令Uα=Vα=∪τα,则U=∏α∈AUα是x在X中的广义开邻域,V=∏α∈AVα是y在X中的广义开邻域.再由子集∪τα(⊆Xα)上的二元运算封闭,即有UV⊆W⊆O.因此X是广义仿拓扑群.
问题8.4无穷多个广义仿拓扑群的广义乘积是否仍是广义仿拓扑群?
推论8.5设对任意α∈A,Xα是强的广义仿拓扑群,Hα是Xα的正规子群,则∏α∈A(Xα/Hα)和∏α∈AXα/∏α∈AHα广义拓扑同构.
证明对任意α∈A,定义映射
φα∶Xα→Xα/Hα,满足φα(xα)=Hαxα,
f∶∏α∈AXα→∏α∈A(Xα/Hα),满足f((xα)α∈A)=(φα(xα))α∈A.
因为φα是满同态,所以f是满同态.
断言1:f是广义开的.
事实上,对任意α∈A,设Eα⊆Xα,则f(∏α∈AEα)=∏α∈Aφα(Eα).由引理6.1知φα是广义开的,所以f是广义开的.
断言2:f是广义连续的.
事实上,对任意α∈A,设Lα⊆Xα/Hα,则f-1(∏α∈ALα)=∏α∈Aφα-1(Lα).由引理6.1,φα是广义连续的,所以f是广义连续的.
断言3:Kerf=∏α∈AHα.
事实上,因为对任意(xα)α∈A∈∏α∈AXα有
(xα)α∈A∈Kerf⟺φα(xα)=Hα,∀α∈A⟺xα∈Hα,∀α∈A⟺(xα)α∈A∈∏α∈AHα,
所以Kerf=∏α∈AHα.
因为f是广义开的广义连续的满同态,所以由定理6.5知∏α∈A(Xα/Hα)和∏α∈AXα/∏α∈AHα广义拓扑同构.
9 广义仿拓扑群的广义紧性
定义9.1设X是广义拓扑空间.X称为广义紧空间,如果X的每一广义开覆盖有有限子覆盖.
引理9.2广义紧空间在广义连续映射下的像是广义紧空间.
证明设X,Y是广义拓扑空间,其中X是广义紧空间,f∶X→Y是广义连续的满映射.设{Uγ}γ∈Γ是Y的广义开覆盖,则{f-1(Uγ)}γ∈Γ是X的广义开覆盖.因为X是广义紧空间,所以存在有限子族{f-1(Uγi)}i=1,…,k覆盖X,从而{Uγi}i=1,…,k是{Uγ}γ∈Γ的有限子族且覆盖Y.故Y是广义紧空间.
定理9.3设X是广义仿拓扑群,g,h∈X.若K是X的广义紧子集,则gKh是广义紧子集.
证明因为X是广义仿拓扑群,定义映射
φ∶X→X,满足φ(x)=gxh,∀x∈X.
由引理3.5知φ是广义连续的,从而由定理9.2知gKh=φ(K)是广义紧空间.

