非负张量谱半径上下界的估计不等式

刘桂敏，张美黎，吕洪斌

(北华大学数学与统计学院，吉林 吉林 132013)

张量的特征值问题有重要的应用背景，如在盲源分离[1]、磁共振成像[2-3]、分子构象[4]等方面都有重要应用.其中，非负张量的特征值和特征向量有许多研究结果[5-8].本文给出一个具有一般形式的非负张量谱半径(最大特征值)的估计不等式.

1 定义及基本结果

如果ai1i2…im≥0，ij=1，2，…，n，j=1，2，…，m，则称为非负张量.我们记所有m阶n维非负张量的集合为.

一个m阶n维张量=(δi1…im)称为单位张量，如果

定义1[5-6]对于m阶n维张量和一个向量x=(x1，x2，…，xn)T，xm-1是一个向量，其第i个分量为

(

如果有λ∈和一个非零向量x=(x1，x2，…，xn)T，使得

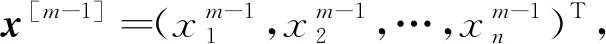
类似于非负矩阵理论，我们称ρ()=sup{|λ|：λ∈σ()}是张量的谱半径，其中σ()是张量的特征值集合.

文献[7]将不可约矩阵的概念推广到张量.

定义2[7]对于m阶n维张量=(ai1i2…im)，如果存在一个非空的真子集I⊂〈n〉，使得

ai1i2…im=0， ∀i1∈I， ∀i2，…，im∉I，

关于非负张量的特征值和特征向量文献[7]给出了如下结果：

定理1[7]设=(ai1i2…im)∈，则存在λ0≥0和一个非负向量x0≠0，使得

(1)

定理2[7]设=(ai1i2…im)∈不可约，则方程(1)中的(λ0，x0)满足：

(ⅰ)λ0>0是的一个特征值.

(ⅱ)x0>0，即x0的所有分量是正的.

(ⅲ)如果λ是的一个具有非负特征向量的特征值，则λ=λ0.此外，在不计倍数的情况下非负特征向量是唯一的.

(ⅳ)如果λ是的特征值，则|λ|≤λ0.

由定理2(ⅱ)和(ⅳ)可知，非负张量的谱半径即是其按模最大特征值.

定义

引理1[9]设=(ai1i2…im)∈，=(ci1i2…im)∈，0≤≤，则ρ()≤ρ().

由引理1我们有

引理2设=(ai1i2…im)∈不可约，则ρ()>ai…i，i∈〈n〉.

文献[9]给出了非负张量谱半径的上下界估计结果：

定理3[9]设=(ai1i2…im)∈，则

文献[10]给出了非负张量谱半径上下界估计的改进结果：

定理4[10]设=(ai1i2…im)∈，且n≥2，则

δ()≤ρ()，

其中

δ()，

δi， j(.

本文给出非负张量谱半径上下界估计的一个具有一般形式的不等式，在特别情况下改进了定理3和定理4.

2 主要结果

定理5设=(ai1i2…im)∈，则

κ()≤ρ()，

其中

κ()，

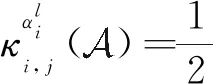
(2)

不失一般性，假设

xt1≥xt2≥…≥xtn-1≥xtn>0.

(ⅰ)首先证明

ρ().

由方程组(2)有

因此，对l∈〈n-1〉，有

(ρ(

r′t1(

即

(ρ()-at1…t1-r′t1(.

(3)

同理，由方程组(2)有

因此

(ρ(.

(4)

(ρ()-at1…t1-r′t1(

因此

ρ(at1…t1+at2…t2+r′t1()+

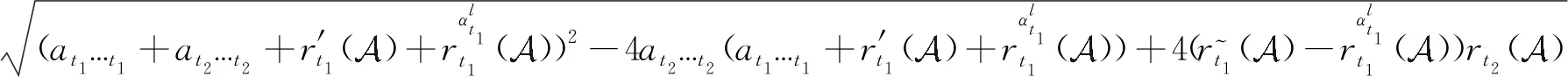
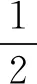
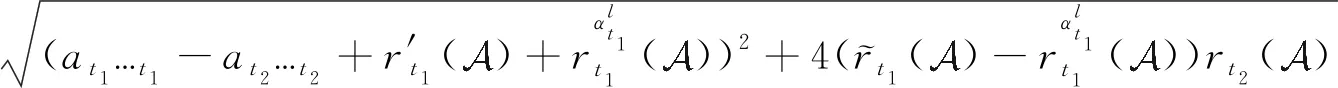
从而有

ρ().

(ⅱ)现在证明

ρ()=κ().

由方程组(2)有

和

与(ⅰ)的证明相似，对l∈〈n-1〉容易得到

ρ().

因此，有

ρ()=κ().

综合(ⅰ)、(ⅱ)有

κ()≤ρ().

其中，

推论1设=(ai1i2…im)∈，且n≥2，则

Δ()≤ρ()，

其中

Δ()，

Δi， j(ai…i+aj…j+r′i(.

3 数值算例

例1设其中

计算知ρ()=10.688 1.由定理3有

10≤ρ()≤13.

由定理4计算有

δ1，2=10.831 0，δ2，1=10.099 0，δ1，3=11.164 4，δ3，1=11.844 3，δ1，4=11.446 2，δ4，1=12.708 2，

δ2，3=10.352 3，δ3，2=11.831 0，δ2，4=10.520 8，δ4，2=12.765 0，δ3，4=12.211 1，δ4，3=12.855 7.

因此

δ(

即有

10.099 0=δ()≤ρ()=12.855 7.

由推论1计算有

Δ1，2=10.577 7，Δ2，1=10.348 5，Δ1，3=11.402 2，Δ3，1=11.639 4，Δ1，4=11.787 1，Δ4，1=12.389 9，

Δ2，3=10.681 1，Δ3，2=11.262 1，Δ2，4=11.000 0，Δ4，2=12.068 4，Δ3，4=12.345 9，Δ4，3=12.700 6.

因此

Δ()}=12.700 6，

即有

10.348 5=Δ()≤ρ()=12.700 6.

因此，定理5的推论1是定理4和定理3的一个很好的改进.