关于一致超图直积的循环指数
2021-05-18 02:36范益政田梦宇
安徽大学学报（自然科学版） 2021年3期
范益政，田梦宇
(安徽大学 数学科学学院, 安徽 合肥 230601)
文献[1-2]独立地引入了张量的特征值.文献[3]引入一致超图的邻接张量表示, 并推广了简单图上的若干谱结论.
定义1
设G
为n
个点v
,v
,…,v
上的m
-一致超图, 其邻接张量定义为m
阶n
维张量(G
)=(a
…), 其中
ρ
()是的特征值, 并且对应唯一的正特征向量(在相差一个常数倍意义下), 且有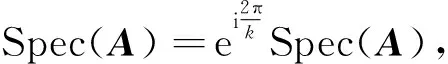
(1)
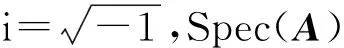
在文献[9]中, 作者定义了一般张量的谱对称性, 并利用张量的广义迹给出了循环指数的显式表示.
定义2
设为张量,l
为正整数.称为谱l
-对称的, 如果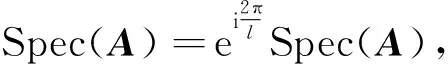
(2)
满足式(2)的最大正整数l
称为的循环指数, 记为c
().一致超图G
称为是谱l
-对称的, 如果其邻接张量(G
)是谱l
-对称的;G
的循环指数定义为其邻接张量(G
)的循环指数, 记为c
(G
). 文献[3]提出研究m
-一致超图的谱m
-对称性. 文献[10]应用张量的广义迹给出m
阶张量的谱m
-对称的刻画. 文献[11]提出研究m
-一致超图的对称谱问题 (即谱2-对称问题). 文献[12]完全刻画了超图的对称谱问题. 文献[13]刻画了m
-一致超图的对称H
-谱问题. 论文主要研究超图直积的谱对称性, 证明G
×H
是谱[c
(G
),c
(H
)]-对称的, 从而[c
(G
),c
(H
)]|c
(G
×H
), 其中[a
,b
]记正整数a
,b
的最小公倍数.1 预备知识
设=(a
…)为m
阶n
维张量. 若的所有元素a
…在其指标的任意置换下仍保持不变, 则称为对称张量; 若的所有元素a
…都非负, 则称为非负张量. 定义的关联有向图D
()如下: 其点集为{1,2,…,n
},弧集为{(i
,i
),…,(i
,i
)|a
…≠0}.D
()可能包含环和多重弧. 张量称为是弱不可约的, 如果D
()是强连通的.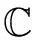
x
-1)=∑,…,∈[]a
…x
…x
,i
∈[n
].定义m
阶n
维单位张量为=(i
…), 其中, 当i
=i
=…=i
∈[n
]时，i
…=1; 否则i
…=0.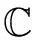
φ
(λ
)定义为多项式系统(λ
-)x
-1的结式， 见文献[1,14-15]. 易见,λ
是的特征值当且仅当它是φ
(λ
)的根. 张量的谱定义为φ
(λ
)的根的多重集, 记为Spec(). 张量的谱半径定义为的所有特征值的最大模, 记为ρ
().文献[16]引入同阶张量的直积的概念, 并给出若干谱结论.
定义4
设和为m
阶且维数分别为n
,n
的张量. 直积⊗定义为m
阶n
n
维的张量, 其元素为(⊗)(,)(,)…(,)=a
…b
…,其中：元素的下标取集合[n
]×[n
]的字典序.设G
=(V
,E
)为一个超图. 超图G
的一个长为t
的链定义为如下点边交错序列v
e
v
e
…e
v
, 其中v
≠v
+1且{v
,v
+1}⊆e
,i
=0,1,…,t
-1. 超图G
称为是连通的, 如果它的任意两点都有一条链连接. 假设G
是m
-一致超图, 则其邻接张量(G
)是非负对称的, 且它是弱不可约当且仅当G
是连通的. 论文中, 一致超图G
的谱、谱半径、特征值和特征向量均指其邻接张量的相应定义. 一致超图G
的谱半径记为ρ
(G
).定义5
设G
和H
为两个m
-一致超图, 则G
和H
的直积, 记为G
×H
, 具有点集V
(G
×H
)=V
(G
)×V
(H
),且{(i
,j
),…,(i
,j
)}∈E
(G
×H
)当且仅当{i
,…,i
}∈E
(G
)且{j
,…,j
}∈E
(H
).引理1
设G
和H
为两个m
-一致超图, 则G
×H
的邻接张量为(G
×H
)=(m
-1)!((G
)⊗(H
)).如果λ
是G
的对应于特征向量x
的特征值,μ
是H
对应于特征向量y
的特征值, 则(m
-1)!λμ
是G
×H
对应于特征向量x
⊗y
的特征值.2 超图直积的循环指数
设G
和H
为两个m
-一致超图. 该节主要讨论G
×H
的循环指数c
(G
×H
)与G
和H
的循环指数c
(G
)和c
(H
)的联系, 证明了[c
(G
),c
(H
)]|c
(G
×H
). 先介绍关于非负弱不可约张量的Perron-Frobenius定理, 其中的一个特征值称为是H
-特征值, 如果它对应一个正特征向量.定理1
设为非负弱不可约张量, 则谱半径ρ
()是的唯一H
-特征值,且对应唯一的正特征向量(在相差一个常数倍意义下).对于m
阶n
维张量, 以及两个n
×n
的对角矩阵,, 根据文献[16]中定义,定义为m
阶n
维张量, 其元素为()…=p
a
…q
…q
.如果=, 则称和-1对角相似， 此时,和-1具有相同的谱.定理2
设和为m
阶n
维实张量, 且||≤, 即|b
…|≤a
…,i
∈[n
],j
∈[m
]. 则(1)ρ
()≤ρ
();
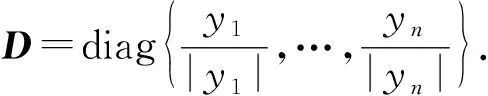
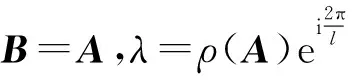
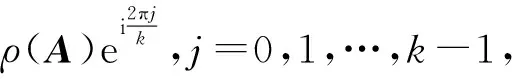
k
即为的循环指数.引理2
设为m
阶张量. 如果是谱l
-对称的, 则l
|c
(); 如果还是对称的, 则l
|m
, 从而c
()|m
.首先讨论超图直积的连通性. 超图G
的2-部分图(2-section), 记为[G
], 定义为点集V
(G
)上的简单图, 其边集为{{u
,v
}|u
≠v
,∃e
∈E
(G
),{u
,v
}⊆e
}, 即两个点在[G
]中相邻当且仅当它们属于G
的同一条边.引理3
设G
和H
为两个m
-一致超图,m
≥3. 则G
×H
是连通的当且仅当G
和H
都是连通的.证明
显然,G
×H
是连通的当且仅当[G
×H
]是连通的.根据文献[18]的引理6.3,[G
×H
]=[G
]×[H
]. 根据文献[19]的定理1, [G
]×[H
]是连通的当且仅当[G
]和[H
]都连通(或等价地,G
和H
都连通), 且至少有一个是非二部图. 由于m
≥3, [G
]和[H
]都含有m
-团(即m
个点上的完全子图), 因而它们都是非二部的. 因此,G
×H
是连通的当且仅当G
和H
都是连通的.定理4
设G
和H
为两个连通的m
-一致超图, 且G
×H
连通. 则G
×H
是谱[c
(G
),c
(H
)]-对称的, 从而[c
(G
),c
(H
)]|c
(G
×H
).证明
由于G
和H
都是连通的, 从而(G
)和(H
)都是弱不可约的. 根据定理1,ρ
(G
)和ρ
(H
)分别为(G
)和(H
)的特征值, 且分别对应于正特征向量x
和y
. 根据引理1, (m
-1)!ρ
(G
)ρ
(H
)是(G
×H
)的特征值, 且对应于正特征向量x
⊗y
. 因此, 根据定理1, (m
-1)!ρ
(G
)ρ
(H
)是G
×H
的谱半径, 即ρ
(G
×H
)=(m
-1)!ρ
(G
)ρ
(H
).(3)
设λ
和μ
分别为(G
)和(H
)的特征值. 根据引理1, (m
-1)!λμ
是G
×H
的特征值, 且|(m
-1)!λμ
|=(m
-1)!|λ
|·|μ
|≤(m
-1)!ρ
(G
)ρ
(H
)=ρ
(G
×H
).(4)
考虑集合
S
∶={|(m
-1)!λμ
|=ρ
(G
×H
)∶λ
∈Spec(G
),μ
∈Spec(H
)}.若|(m
-1)!λμ
|=ρ
(G
×H
), 根据式(4), |λ
|=ρ
(G
)且|μ
|=ρ
(H
). 根据定理3,可得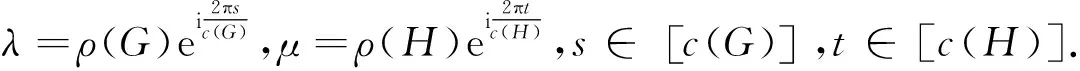
设
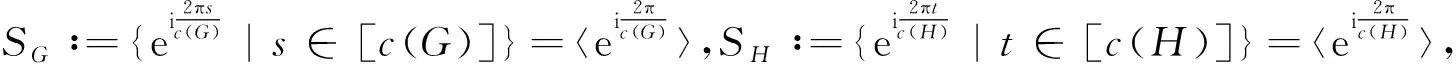
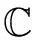
S
|=|S
·S
|=∶β
,
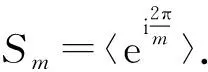
c
(G
),c
(H
)]|β
.(5)
因为c
(G
)·c
(H
)=[c
(G
),c
(H
)]·(c
(G
),c
(H
)), 其中(a
,b
)记正整数a
,b
的最大公约数, 故S
·S
的任一个元素都可以表示为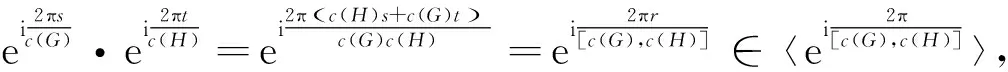
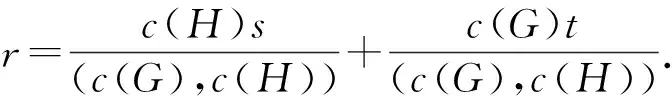
β
|[c
(G
),c
(H
)]，(6)
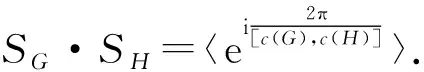
推论1
设G
和H
为两个连通的m
-一致超图, 且G
×H
连通. 如果c
(G
)=m
或者c
(H
)=m
, 则c
(G
×H
)=m
.证明
根据引理2,c
(G
)|m
且c
(H
)|m
. 如果c
(G
)=m
或者c
(H
)=m
, 则[c
(G
),c
(H
)]=m
. 根据定理4, [c
(G
),c
(H
)]|c
(G
×H
), 从而m
|c
(G
×H
). 而根据引理2,c
(G
×H
)|m
, 故结论成立.推论2
设G
为连通m
-一致超图,e
为仅由有一条边构成的m
-一致超图, 且G
×e
连通. 则c
(G
×e
)=m
.证明
根据文献[3]或[10]的结论,c
(e
)=m
. 故根据推论1, 结论成立.在定理4及推论1和2中, 如果m
≥3, 根据引理3, 显然G
×H
或G
×e
连通. 在推论2中, 当m
=2, 即G
为连通简单图, 并且假设G
为非二部图, 则根据文献[19]的结论,G
×e
连通, 此时G
×e
也是G
的双覆盖(double cover). 根据推论2,c
(G
×e
)=2, 从而根据非负矩阵的Perron-Frobenius定理,G
×e
为二部图.猜你喜欢
中学生理科应试(2021年11期)2021-12-09
语数外学习·高中版中旬(2020年3期)2020-09-10
数学学习与研究(2018年15期)2018-11-12
课程教育研究·新教师教学(2016年18期)2017-04-12
数学学习与研究(2016年19期)2016-11-22
电脑知识与技术(2016年22期)2016-10-31
科技经济市场(2014年11期)2014-12-30
学生之友·最作文(2014年6期)2014-07-24
数学大世界·初中生辅导版(2010年2期)2010-03-08
数理化学习·高三版(2009年4期)2009-04-27
