次酉极因子的扰动界
2021-05-18 02:35:48涂媛媛尚旭东
安徽大学学报(自然科学版) 2021年3期
涂媛媛,尚旭东
(南京师范大学泰州学院 数学科学与应用学院,江苏 泰州 225300)

F
范数下新的扰动界,并与文献[1]中取F
范数时的结果进行比较,发现论文的结果改进了原有结论,并利用文献[2]中新的换子不等式,对李仁仓的研究结论重新给出证明,论文的证明更加简洁.定义
设∈×,有分解=,(1)
若∈×是次酉矩阵,∈×为半正定阵,则这一分解叫作的广义极分解. 当r
<n
时,因子是不唯一的.
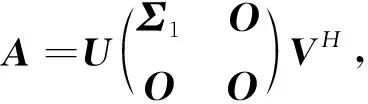
(2)

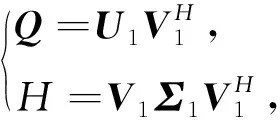
(3)
则=是的广义极分解.
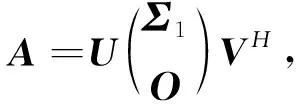
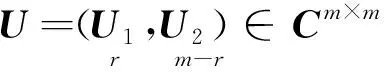

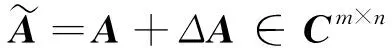
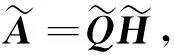
(4)
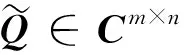
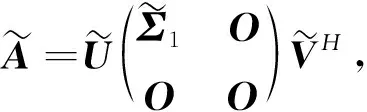
(5)
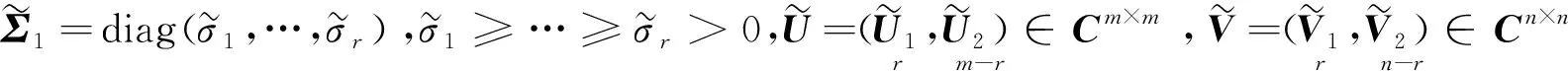

(6)
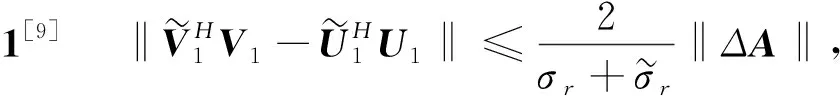

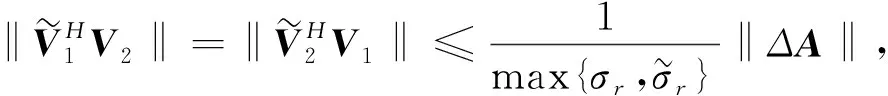
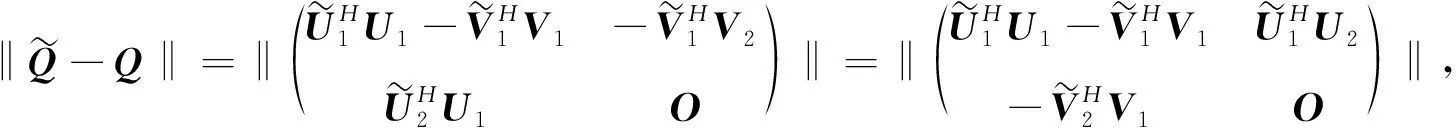
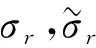
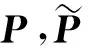
Δ
=[α
,β
]⊂,Δ
′=/(α
-δ
,β
+δ
),δ
>0.
δ
,
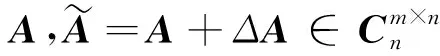
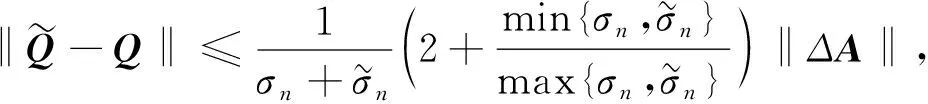
(7)

引理4
设∈×,∈×是正规矩阵,并且
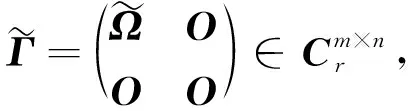
δ
,…,δ
)≥,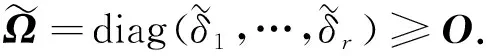
d
()-d
()≥,i
=1,2,…,r
,(8)
则
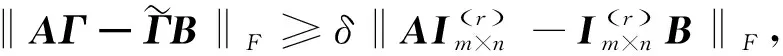
(9)

1 主要结果

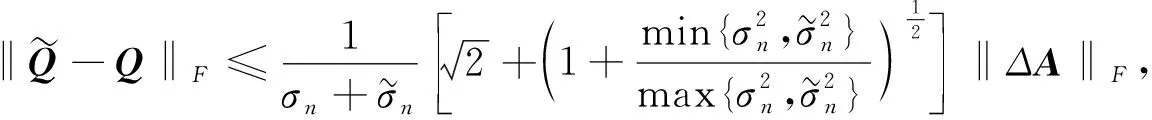
(10)


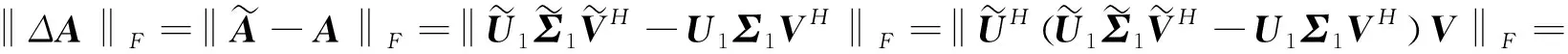


又
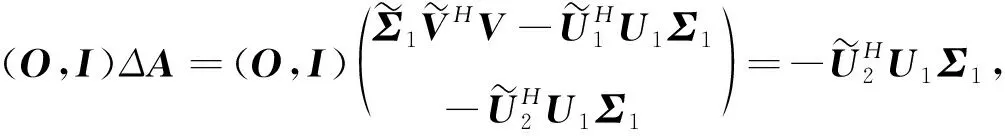
所以,有
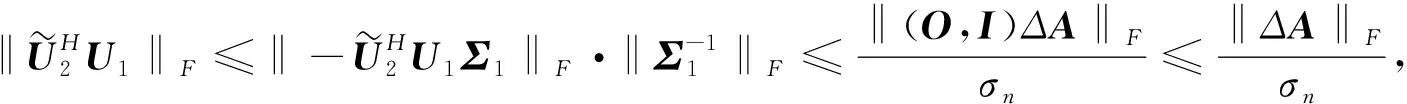
同理可得
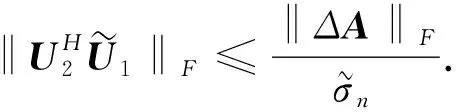
因而
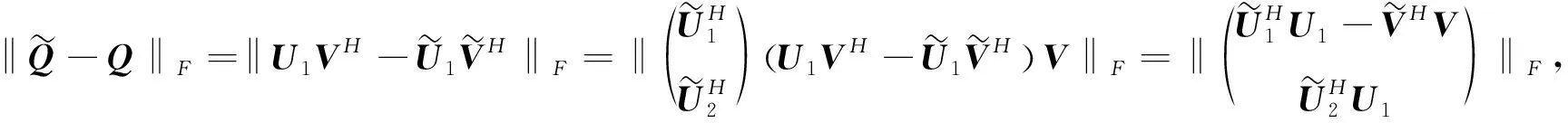
令
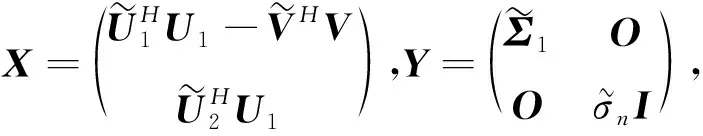
则

且

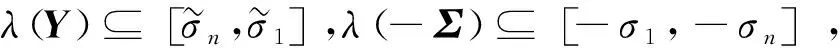
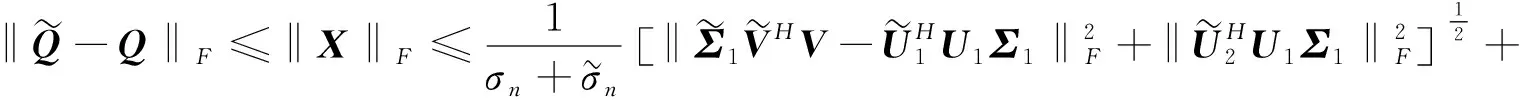


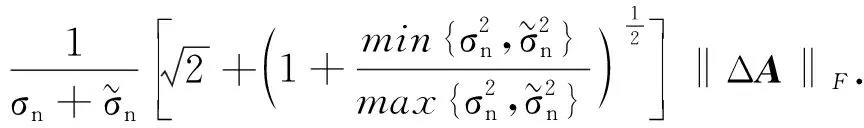
证毕.
注
当引理3中酉不变范数取F
范数时,其结果为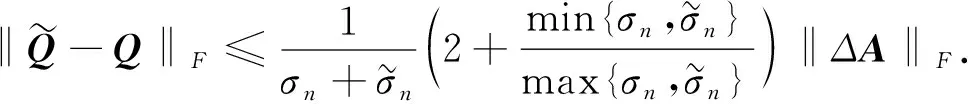
(11)
比较(11),(10)式,有
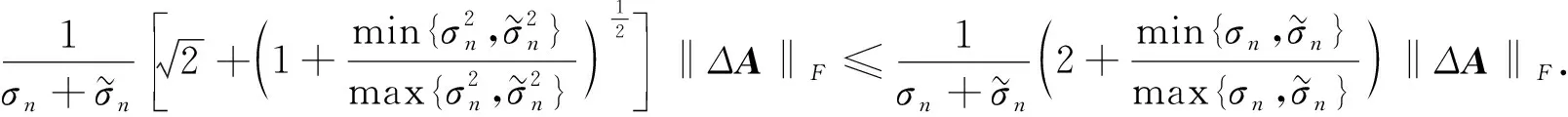
F
范数的情况下改进了文献[1]中定理3.1的结果.
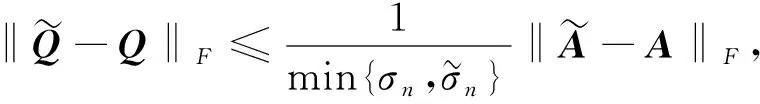
其中
=,
需要说明的是,该结论已由李仁仓在文献[6]给出,论文下面给出简短的证明.
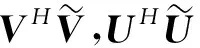
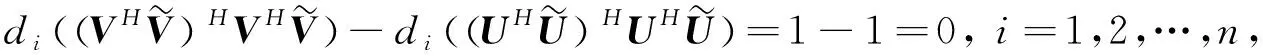

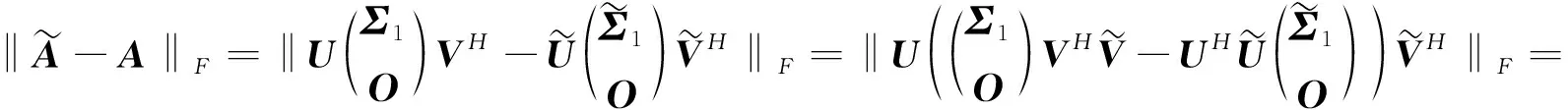

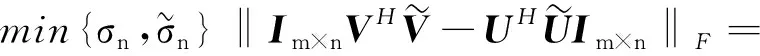

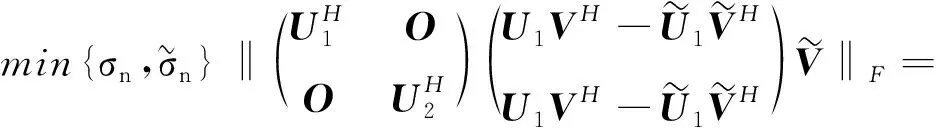
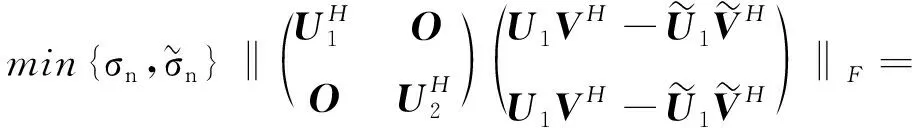
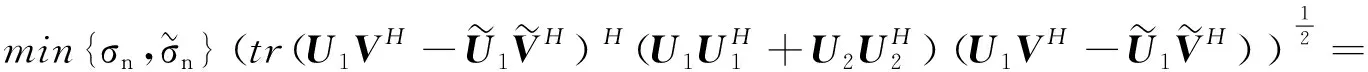

即
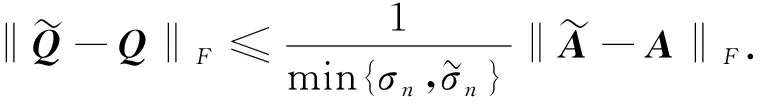
猜你喜欢
数学物理学报(2022年4期)2022-08-22 04:06:36
数学物理学报(2022年3期)2022-05-25 13:33:00
数学物理学报(2019年4期)2019-10-10 02:38:56
中国中医急症(2019年10期)2019-05-21 07:20:28
中国校外教育(下旬)(2017年8期)2017-10-30 17:32:36
数学物理学报(2017年3期)2017-07-01 16:18:48
贵州师范学院学报(2016年3期)2016-12-01 03:53:52
数学年刊A辑(中文版)(2016年2期)2016-10-30 01:46:38
电源技术(2015年11期)2015-08-22 08:50:38
数学年刊A辑(中文版)(2014年1期)2014-10-30 01:48:06

