基于双群体伪并行GA-DE多目标算法的动态环境经济调度

李笑竹，王维庆*，徐其丹

(1.新疆大学 可再生能源发电与并网技术教育部工程研究中心，新疆 乌鲁木齐 830047；2.国网新疆电力有限公司 经济技术研究院，新疆 乌鲁木齐 830000)

动态环境经济调度 (dynamic environment economic dispatch, 简称DEED)具有高纬度、非线性、非凸等特征，且包含复杂的约束条件，目前对DEED的研究主要集中于模型求解.文献[1]利用价格惩罚因子(PPFs)，将多目标DEED转变为单目标DEED，采用万有引力启发式搜索算法对转化后的单目标DEED进行求解.文献[2]采用加权和半正定规划策略，对多目标进行转化，然后通过调节各目标权值求解.虽然上述求解方法效率高、速度快，但对目标函数要求过高，若为不可微的非凸形式则无法求解，且解对初值的选取较敏感，易陷入局部最优，难以得到真正的帕累托优化前沿(Pareto-optimal front, 简称PF).基于此，很多研究人员将DEED作为多目标优化直接求解.根据产生新解的方式，现有多目标算法可分为以下3类：①通过遗传算法产生新解的多目标算法，如文献[3]提出的基于非支配序列的遗传算法Ⅱ(non-dominated sorting genetic algorithms Ⅱ,简称NSGA-Ⅱ)，文献[4]提出的改进的NSGA-Ⅱ，这类算法综合性能较稳定.②通过粒子群算法产生新解的多目标算法，如MOPSO (multi-objective particle swarm optimization)，SMPSO(speed constrained multi-objective particle swarm optimization)，DE-PSO(differential evolution-particle swarm optimization)算法.③通过差分进化算法产生新解的多目标算法，如改进的自适应多目标差分进化算法、基于分解的多目标进化算法(multi-objective evolutionary algorithm based on decomposition, 简称MOEA/D)，这类算法在处理复杂问题时有较好效果，且已成功应用于多个领域.

该文提出一种双群体伪并行GA-DE(genetic algorithm-differential evolution)多目标 (double swarm peudo pallelism multi-objective GA-DE, 简称DSPPMO-GA-DE) 算法求解DEED模型.该算法基于外部精英保留和Pareto占优概念，采用平均熵和立方混沌映射初始化策略，获得较为优质的初始种群；利用差分进化算法和遗传算法，构建双种群协同进化模式；通过进化模式不同的种群间交流学习和最优值共享的策略，实现种群协同搜索；为避免算法后期出现“早熟”现象、陷入局部最优解，在差分进化算法中加入控制参数自适应策略及禁忌搜索策略；采用改进的Pareto解集裁剪方式，对外部精英存档进行裁剪；利用各维动态松弛约束机制处理DEED模型的复杂约束条件；从模糊理论的最佳折中得到一个Pareto最优解.该文考虑燃机消耗、污染排放、损耗间的矛盾，将发电机容量、功率平衡及发电机爬坡作为约束条件，建立3目标DEED模型.最后，使用10机组系统验证所提算法的可行性.

1 电力系统DEED模型

1.1 目标函数

(1) 燃料成本.考虑域点效应，得到燃料成本为

(1)

(2) 排放量.为不失一般性，该文考虑发电过程中排放的所有污染.污染排放量与发电机有功输出间的关系为

(2)

其中：

E

(

P

)为发电的污染排放量；

α

，

β

，

γ

，

ξ

，

λ

为第

i

台发电机的排污特性系数.

(3) 线损.电力系统传输网络的线路损耗与发电机有功输出间的函数关系可表示为

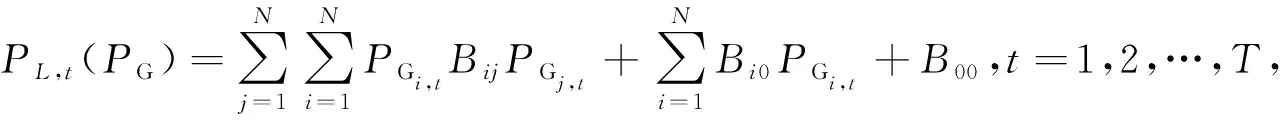
(3)

其中：

P

,(

P

)为电力系统传输网络的线路损耗；

B

，

B

0，

B

为传输损耗系数.

1.2 约束条件

(1) 发电容量约束.为了运行稳定，须限制发电机有功输出在其最小、最大值之间，即

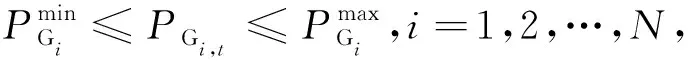
(4)

(2) 功率平衡约束.总发电量必须满足总需求

P

D,和网络的有功功率损耗

P

，即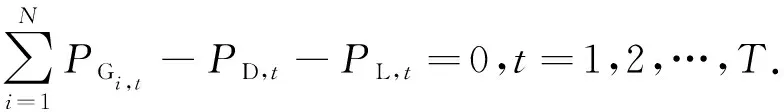

(5)

(3) 发电机爬坡约束.由于建立的模型为动态调度模型，因此对于每台发电机在相邻时刻输出功率的变化率不能超过发电机输出功率上升、下降率，即

D

R≤

P

G,-

P

G,-1≤

U

R，

(6)

其中：

D

R，

U

R分别为第

i

台发电机在单位时段 (1 h)输出功率的最大上升、下降率.

2 双群体伪并行GA-DE多目标算法

2.1 双群体伪并行

该文提出的DSPPMO-GA-DE算法中，一个种群采用改进的DE(differential evolution)，另一个种群采用GA(genetic algorithm).进化过程中，种群间在适当时间交换信息，使多样性加速进化.由于每一种群并未同时执行进化，仍以串行方式顺序执行，故称之为伪并行DE-GA多目标算法.

DE易操作，全局搜索能力及鲁棒性较强.为统筹考虑算法的收敛速度与种群的多样性，该文选取DE/best/2为变异策略.变异后的下一代个体为

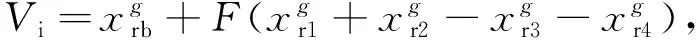
(7)

DE/best/2策略的收敛速度快，但易出现陷入局部最优解的情况.为克服此不足，引入“局部搜索”性能较为突出的禁忌搜索(tabu search, 简称TS)策略.TS策略的优点为在搜索空间可接受劣解，不足为对初始解有较强的依赖.鉴于传统的DE及TS的缺点，该文采用2阶段混合算法.第1阶段使用DE进行全局搜索，收敛到一定程度并陷入“停滞”后，执行第2阶段的TS局部搜索.将DE得到的结果作为TS的初始解，能克服较差初始解降低TS收敛速度的不足.

2.2 协同策略

为增加初始种群的多样性，采用平均熵及立方混沌映射策略对种群进行初始化.在种群的个体编码中加入控制参数，能基于多目标优化特征对控制参数进行自适应调整.

2.2.1 平均熵初始化

使用平均熵初始化策略，可以得到多样性充足、在搜索空间分布均匀的初始解.设初始种群有NP个个体，维数为

D

.根据信息论，群体熵

H

的表达式为

(8)

其中：

m

为初始化种群中已知的个体数量，

k

为初始化过程中产生的新解数量，

P

是第

i

个个体的任意2维变量间的相似程度，其表达式为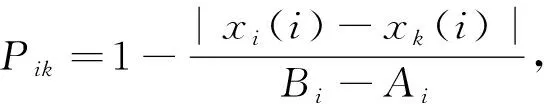

(9)

其中：

A

为第

i

维变量的上限，

B

为第

i

维变量的下限.

平均熵初始化步骤如下：

(1) 随机产生3个已知个体；

(2) 随机产生新个体；

(3) 利用(8)～(9)式算出新种群平均熵，如果新个体的阈值大于设定值则将其加入初始化种群，如此反复直至获得NP个个体.

2.2.2 立方混沌映射初始化

研究表明立方混沌映射比Logistic混沌映射具有更好的历遍性及更均匀的分布性，因此采用立方混沌映射对DE的种群进行初始化.立方混沌映射为

y

(

n

+1)=4

y

(

n

)-3

y

(

n

)， -1<

y

(

n

)<1，

y

(

n

)≠0，

n

=0,1,2,….

(10)

设初始种群有NP个个体，维数为

D

.先随机产生一个在[-1,1]的

D

维变量作为个体1；再用式(10)对个体1的各维进行NP-1次迭代，产生NP×

D

的变量矩阵；最后，利用下式将立方混沌映射产生的在[-1,1]的变量映射到解区间[

x

，

x

max]

(11)

其中：

y

为由式(10)产生的混沌变量，

x

为映射得到的混沌变量.

2.2.3 参数自适应调整

使控制参数CR及

F

参与个体编码.每代的个体

x

都有属于自己的CR及

F

，更新方式如下

F

=

F

+rand(

F

-

F

)，CR=CR+rand(CR-CR)，

(12)

其中：rand，rand为[0,1]上均匀分布的随机数；

F

，

F

分别为变异常数的上、下限；CR，CR分别为交叉概率常数的上、下限.该文中，取

F

=0.1，

F

=0.9，CR=0.0，CR=0.5.

2.3 双群体伪并行GA-DE多目标算法

多目标优化涉及多目标在各自约束条件下同时达到各目标的最小或最大，希望获得一组具有足够多样性且均匀分布在整个Pareto前沿的最优解.DSPPMO-GA-DE算法为保持最优解集的多样性，通过拥挤熵策略对外部精英存档进行裁剪，拥挤熵较常用的拥挤距离能更加准确描述解间的拥挤程度.

2.3.1 基于拥挤熵的多样性保持策略

拥挤熵为拥挤距离与分布熵的结合.目标空间中，分布熵的表达式为

E

=-[

p

log

p

+

p

log

p

]，

(13)

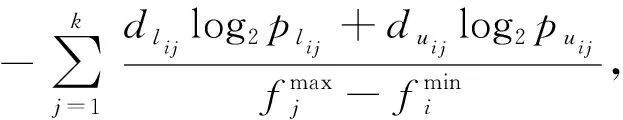
(14)

2.3.2 占优选择算子

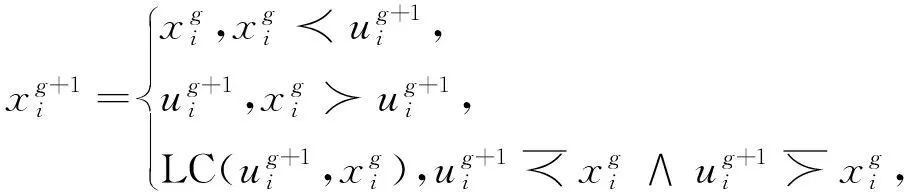
(15)

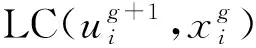
3 DSPPMO-GA-DE算法在DEED模型上的应用

3.1 复杂约束条件的处理

步骤1 计算得到不可行解，其表达式为

(16)

步骤2 判断各时刻(16)中的

P

=[

P

G1,,

P

G2,,…,

P

G,]是否满足等式约束(5)，若不满足，则对各维变量进行动态松弛调节.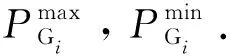

步骤4 利用下式判断是否满足功率平衡约束

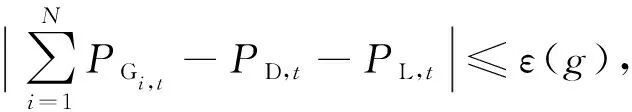
(17)

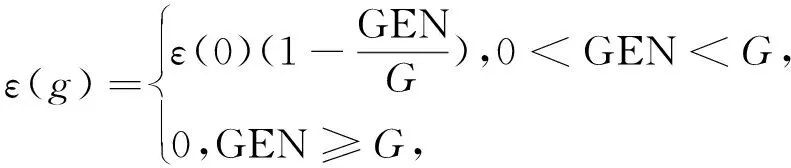
(18)

其中：

ε

(0)=10.若不满足(17)式则执行步骤5，否则转步骤6.

步骤5 对不可行解利用

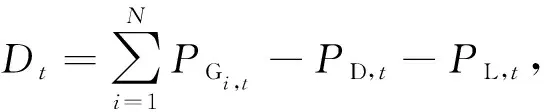
(19)

计算违反等式约束的程度.通过

(20)

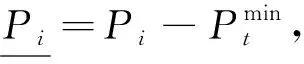
(21)

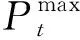
(22)

通过对不可行解的调整，可得

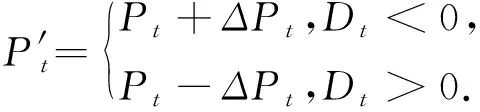
(23)

然后，将

P

′作为该时刻的解.步骤6 设置

t

=

t

+1,将下一时刻

P

G,的最大、最小值更新为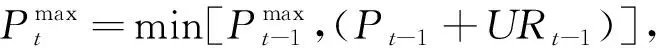

(24)

步骤7 重复步骤Step 2.2～ 2.4 直至

t

=

T

.步骤8 返回矩阵.

3.2 算例分析

使用10机组系统验证DSPPMO-GA-DE算法在DEED模型上的可行性.算例中机组煤耗参数、污染排放参数、出力限制、爬坡速率限制、网损系数、负荷预测等数据源自文献[4].为了证明DSPPMO-GA-DE算法的可行性，通过包含2个优化目标(燃料成本及污染排放)的动态经济环境调度模型(模型1)进行仿真验证.表1为DSPPMO-GA-DE得到的模型1的最佳折中解.从表1可看出： DSPPMO-GA-DE可同时优化燃料成本和排放这两个目标；能有效处理调度过程中的功率平衡约束.

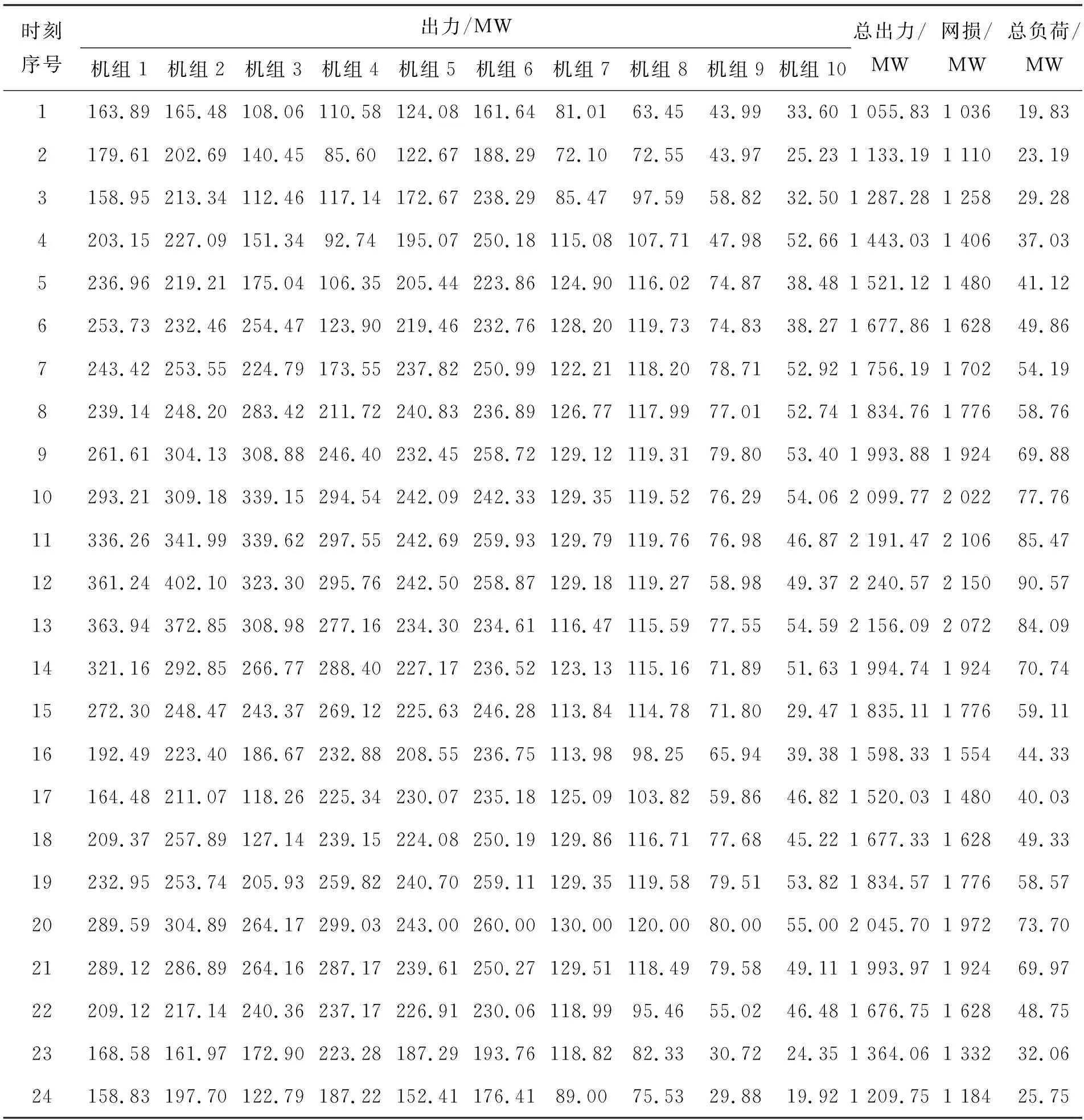
表1 DSPPMO-GA-DE得到的模型1的最佳折中解

为验证DSPPMO-GA-DE的可行性，将DSPPMO-GA-DE得到的相关结果与改进的NSGA-Ⅱ、动态约束处理的改进多目标差分进化算法(enhanced multi-objective differential evolutionary algorithm with dynamic constraints handling，简称EMODEDCH)、改进的PSO、改进的MOEA/D进行比较.表2为多种算法最优折中解对应的燃料成本、污染排放的比较.

表2 多种算法最优折中解对应的燃料成本、排放比较

由表2可知：DSPPMO-GA-DE得到了更小的燃料成本和污染排放；与改进的PSO、改进的MOEA/D相比，虽DSPPMO-GA-DE的燃料成本提高了一点，但污染排放要远低于这两种算法.可见，DSPPMO-GA-DE获得了最为满意的折中解且能同时优化燃料成本和污染排放.

下面将线损作为优化目标加入优化调度模型，得到包含3个优化目标(燃料成本、污染排放及线损)的动态经济环境调度模型(模型2).表3为DSPPMO-GA-DE得到的模型2的最佳折中解.由表3可知，DSPPMO-GA-DE能同时优化调度成本、污染排放及线损3个目标，且能保证功率平衡.

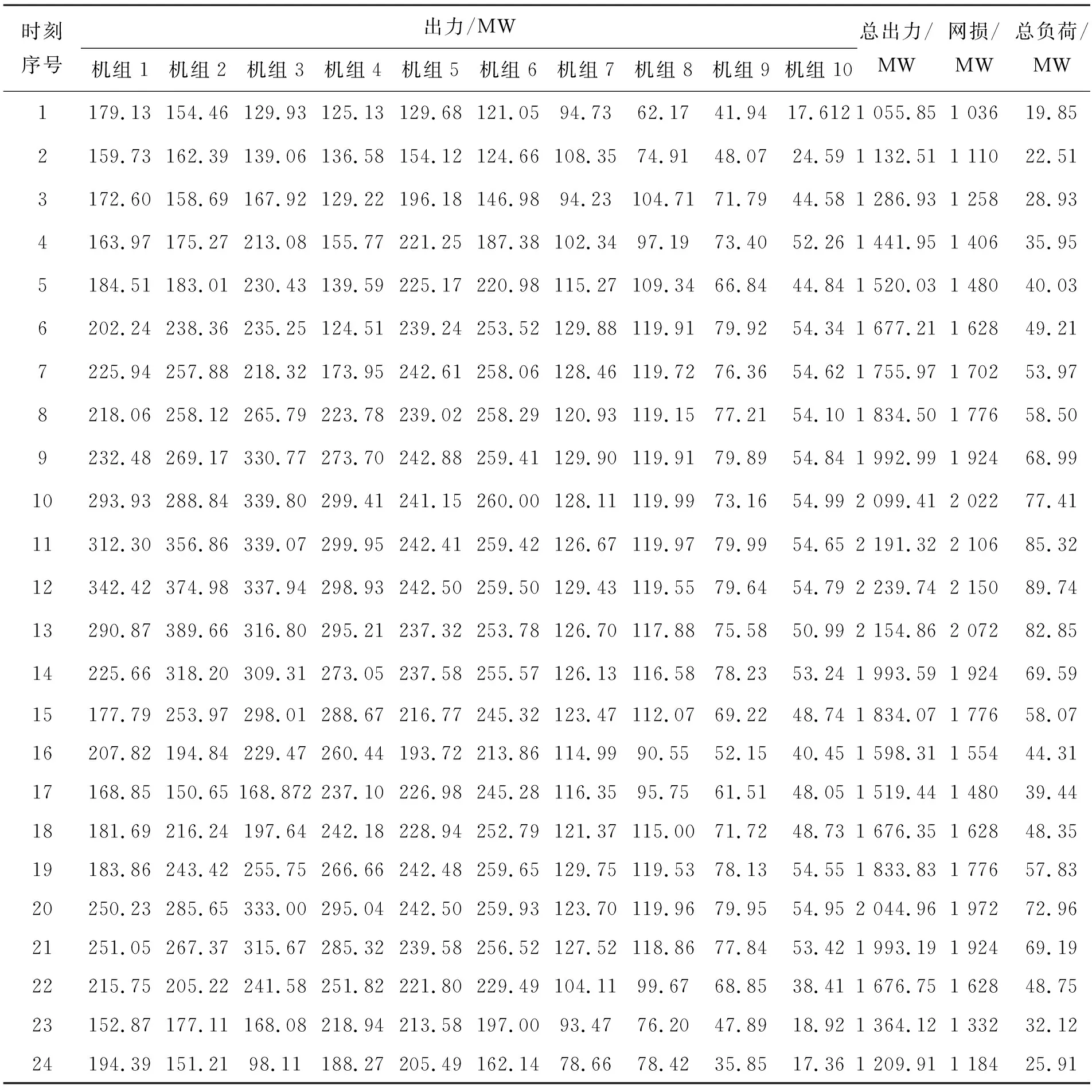
表3 DSPPMO-GA-DE得到的模型2的最佳折中解

表4为模型1，2的最优折中解对应的燃料成本、污染排放、网损比较.由表4可知，模型2的污染排放相对模型1只升高了0.771%，而燃料成本和线损分别降低了2.163%和1.180%.可见，模型2得到了更加满意的折中解.因此，将线损作为优化目标引入DEED模型，建立包含经济、环境和线损的3目标的DEED多目标优化模型具有一定的经济价值.

表4 模型1，2的最优折中解对应的燃料成本、污染排放、网损比较

4 结束语

笔者提出了一种双群体伪并行GA-DE多目标算法，10机组系统验证结果表明该算法具有可行性.在燃料成本、污染排放之后再加入线损作为优化目标的DEED模型，较传统模型能获得更为满意的折中解.分析多目标优化问题时发现，现有多目标优化算法在进行高维目标优化时，均存在保持解的多样性的能力不强，提出克服此不足的新算法为笔者后续研究内容.