圆锥曲线中一个完美交点性质的简证及再探究

安徽省涡阳第一中学(233600)丁猛 贾其源

安徽省合肥市第八中学合肥市蒲荣飞教育名师工作室(230071)蒲荣飞

文[1]探究得到了椭圆中一个完美交点具有如下性质:

性质如图1,椭圆C:的右焦点为F,右准线l与x轴交于点N,AB为垂直于x轴的动弦,直线AF与BN交于点M,则点M恒在椭圆C上.

然后又将其类比到双曲线和抛物线,得到

性质1如图2,圆锥曲线C的焦点为F,该焦点对应的准线l与其对称轴交于点N,AB为垂直于该对称轴的动弦,直线AF与BN交于点M,则点M恒在圆锥曲线C上.

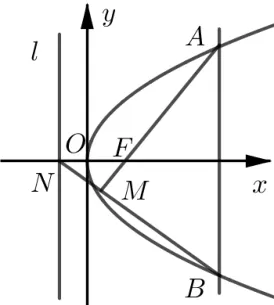
图2

文[2]在此基础上进行了变式研究,得到

性质2如图2,圆锥曲线C的焦点为F,该焦点对应的准线l与其对称轴交于点N,AB为垂直于该对称轴的动弦,直线AF与圆锥曲线的另一交点为M,则直线BM必过定点N.

针对以上两个性质,两文均使用了解析法,证明过程较为繁复.本文拟先给出一种较为简洁的平几证法,然后再给出另一个变式性质,供参考.

1 平几简证

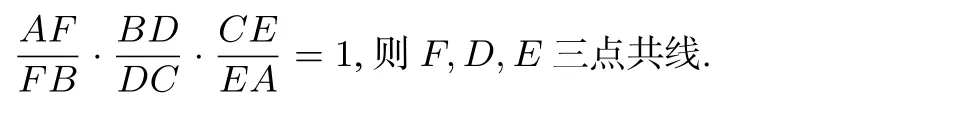
图3

图4

图5

故由Menelaus 逆定理知B,M,N三点共线.

2 变式性质

对性质1,2 继续进行变式探究,可以得到

性质3如图6,圆锥曲线C的焦点为F,该焦点对应的准线l与其对称轴交于点N,过焦点F的直线与曲线C交于A,M两点,直线MN与过点A且与对称轴垂直的直线交于点B,则点B恒在圆锥曲线C上.

图6