小学数学核心素养选谈（之二）

摘要：量感、符号意识、运算能力是小学数学“数与代数“领域中具有代表性的数学核心素养。量感的发展，要丰富感性经验，建立度量意识，并突出比较操作，刻画度量单位，同时将精确测量与估量相结合，提升度量能力。符号意识的发展，则要从直观到抽象，理解符号的内涵，同时注重比较，感受符号的简洁便利，并在运用中体会符号的优势。运算能力的发展，要基于情境，理解算理，掌握算法，并且推理论证，“发现”算法，同时培养估算意识。

关键词：数学核心素养;量感;符号意识;运算能力

本文系宿迁学院基础教育研究2021年度专项课题“基础教育阶段学生数学学科核心素养的培养与发展”（编号：2021jyjc04）、宿迁市教育学会“十四五”规划2021年度一般课题“数学学科核心素养视阈下PBL的小学数学教学设计研究”（编号：XHLX2021256）的阶段性研究成果。在《小学数学核心素养选谈（之一）》参见：殷如意，朱沛雨.小学数学核心素养选谈（之一）[J].教育研究与评论，2021（5）。一文中，笔者分别选取了小学数学“数与代数”“图形与几何”“统计与概率”“综合与实践”领域中较具代表性的数感、空间观念、数据观念、应用意识做了解读。“数与代数”领域内容在小学数学中占比最多，是根基所在，对其他领域的学习有着重要影响，可以说是培养学生数学核心素养的关键领地。因此，本文继续选取“数与代数”领域中较为重要的量感、符号意识、运算能力素养加以解读，并谈谈具体的发展路径。

一、 “量感”及其发展

（一） 对“量感”的解读

《义务教育數学课程标准（2011年版）》（以下简称《课标》）中并未单独给出“量感”一词，而是将其作为数感的一部分，强调了数量、数量关系，因为量感通常依附于数的表达。然而在近十年的数学课程、教学改革推进中，“量感”一词被反复提起、强调。义务教育数学课程标准修订的预审稿中，“量感”一词赫然在列，突出了其在数学学习、学生发展中的独特作用。

2021年5月20日，史宁中教授在全国新世纪小学数学课程与教学系列研讨会上强调，数感和量感的本质都是数的表达，但是在谈“数感”时，可以把数量中的后缀量词去掉，而谈“量感”时，计量单位不可以去掉，数感表达的数与量感表达的数本质是不一样的。

何为“量感”？国内对“量感”概念的解读一直较为模糊。就字面意思而言，量感同数感相同，属于一种直觉，是个体对物体的大小、多少、轻重、厚薄等属性的直接感受力、辨别力，如蚂蚁之小、虎鲸之大，棉花之轻、铁块之重等。陈静.儿童“量感”素养的理性审视、问题剖析及培养策略——以三、 四年级学生为例[J].小学教学研究，2021（10）：6。这样的理解中，量感包含了个体对“量”的直觉感悟和内在推断。李星云教授从量感发展的表现出发，认为个体量感的发展，应表现为能够感知事物的可测量属性及相互关系;能够理解度量的现实意义及统一度量单位的必要性;能够在现实世界中恰当选用不同度量工具、单位进行度量与转化;能够理解并运用估量、估测。李星云.论小学生量感的认识及培养策略[J].内蒙古师范大学学报（教育科学版），2021（5）：147。这样的理解，强调了量的感知、度量技能、估量。孙思雨等人通过量感与数感的比较研究，认为“量感”是指“学生关于量的比较、运算和估计等方面的感悟”。孙思雨，孔企平.“量感”的内涵及培养策略[J].小学数学教师，2021（7）：45。这突出了单位之间的换算、比较以及估测。梁培斌认为，“量感”指的是学生在实际情境中主动地、自觉地理解和运用“量”的态度和意识。梁培斌.小学数学量感可视化教学探索[J].教学与管理，2019（10）：40。这指出了量感对个体敏感性的要求。

比较诸多学者对量感概念的研究，越来越多的学者将量感独立于数感之外进行概念界定，在承认量感与数感依附意义的同时，更肯定量感自身的发展价值。笔者以为，对于量感的理解，可从三个方面出发：一是形成度量意识，能够自觉对量及其关系进行判断与推断;二是理解度量单位，理解不同度量单位的内涵及相互关系，能够恰当选用度量单位及度量工具;三是掌握度量策略，包括精确的度量技能及估量。

（二） “量感”如何发展

1. 丰富感性经验，建立度量意识。

数学核心素养可概括为用数学的眼光、思维、语言沟通数学与现实生活，其本质强调了数学与生活的一致性——学生通过数学学习能够形成一种习惯、自觉意识或是直觉，当生活场景中包含数学信息、产生数学需求时，个体能够主动提取出自身认识中相关的数学信息、问题、措施等。因此，促进学生量感发展的首要因素是基于生活情境的度量意识培养。

度量意识的建立尤其要让学生从视觉、听觉、触觉等多个感官层面感受到量在现实生活中的普遍存在，丰富学生对于量的感、知觉经验，让学生体验、理解不同量的含义与区别，理解面对不同的物体、事件、场景要选择不同类型的度量单位，以及在同一类型度量单位下选择不同级别的度量单位和工具。

比如，苏教版小学数学一年级上册《比一比》的教学中，对于“长短”“高矮”“轻重”“多少”“远近”等事物属性的量的认识，是学生储备对量的感性认识的重要契机，是发展学生度量意识的基础。教学中，教师要引导学生通过看一看、拉一拉、比一比、称一称等多样化的操作活动，获得直观的、直接的量的认识基础，知道事物的不同属性可以用不同的方式进行量的表达，了解“长短”“高矮”“远近”的使用区别。同时，引导学生使用这些词来描绘生活中的事物、现象等，启发学生用度量的眼光、从度量的角度去认识现实世界。

2. 突出比较操作，刻画度量单位。

在实际生活中，学生能够积累丰富的量的经验。而在数学学习的过程中，学生要能够感受到不同量的区别，要能够产生统一度量单位的需要，要学会选用不同的度量单位与度量工具。数学学习中，度量单位概念的形成是学生量感形成的关键，是学生基于不同的事物属性选用度量工具、开展度量活动的前提。

度量单位概念在学生头脑中的刻画，需要经历由直观到抽象、由表象到概念的逐步数学化、符号化过程，即经历“再创造”的过程。教师在教学中要注意通过创设真实的度量问题情境，启发学生在看一看、比一比、量一量、画一画等操作活动中，经历选用度量单位、度量工具、度量方法的过程，帮助学生形成清晰的度量单位关系图。

比如，在质量单位“千克和克”的学习中，教师可引导学生经历掂一掂、称一称、再掂一掂的三步活动，初步建立千克的概念，理解1千克到底有多重。第一步，掂一掂。提供体积相仿的薯片、红枣各一包，学生通过掂一掂感受轻与重。基于学生的直接感受，教师引入“称一般物体的重量用千克作单位，称较轻物体的重量用克作单位”。由此，学生结合亲身体验，实际比较，理解同是质量单位的千克与克的区别。第二步，称一称。学生在掂一掂的基础上称一称，通过台秤指针的转动，建立1千克的概念。第三步，再掂一掂。学生带着所建立的1千克的概念，再次掂一掂，将1千克的概念与1千克的重量建立联系，感受并体会1千克的重量。

3. 将精确测量与估量相结合，提升度量能力。

精确测量是数学学习需要形成的重要技能，是科学研究的基础。而估量是生活测量的常用方式，估量既是量感发展的重要手段，也是量感发展的主要表现。这就要求教师在教学中首先引导学生学会基于不同的问题需求选择不同的测量方式，组织学生在实际的问题情境中开展估量活动、选择估量策略，提升估量的准确性。同时，引导学生在不同的问题情境中产生精确测量的需求，恰当选用测量工具，掌握测量方法。其中，估量能力的发展，要由外走向内，形成一种本能的判断力，形成“肌肉记忆”。在这个过程中，要引导学生在操作的基础上，分析、比较、想象、判断，由动手操作走向深度的动脑思考，不断丰富对事物量的感受，不断修正对量的大小的感觉，经历理性思辨的思维历程。陈静.儿童“量感”素养的理性审视、问题剖析及培养策略——以三、 四年级学生为例[J].小学教学研究，2021（10）：8。在度量能力培养的过程中，应坚持估量与精确测量相促进的原则，可引导学生“先估再量”。这样，既能够发展学生的估量意识与能力，也能够通过精确结果验证估量结果、调整估量误差。

比如，在质量单位“1千克”的概念建立过程中，教师可组织学生在上文三个步骤的基础上，开展估重和精准称重的活动，进一步加强学生对“1千克”重量的感受，同时发展估重与称重的度量能力。第四步，估一估。学生在初步建立1千克概念的基础上，通过倒入、取出的反复活动，在塑料袋中装入大约1千克的大米（通过掂一掂的方式自主判断，使重量尽可能接近1千克）。第五步，称一称。当学生判断自己袋子里大米的重量接近1千克后，再称一称，得到精确的重量，理解估量与精确测量的误差。同时，引导学生理解：想要购买1千克左右的大米时可以进行估量，而想要确定买了多少千克大米、要付多少钱时，需要精确测量。

再如，在引导学生建立“1分钟”的概念时，教师可以让学生描述1分钟可以做什么事来估计、想象1分钟的长短，也可以组织1分钟的口算活动、测量活动来帮助学生体会、验证1分钟的长短。

二、 “符号意识”及其发展

（一） 对“符号意识”的解读

《课标》指出，符号意识主要是指能够理解并且运用符号表示数、数量关系和变化规律;知道使用符号可以进行运算和推理，得到的结论具有一般性。中华人民共和国教育部.义务教育数学课程标准（2011年版）[S].北京：北京师范大学出版社，2012：6。这对个体符号意识发展的目标、具体表现做了阐述。综合分析国内学者的相关研究，关于符号意识的理解也是各有侧重。有人认为，符号意识的发展主要表现为用符号表示和运算。王强国.符号意识的内涵、偏颇及教学要领[J].中小学教师培训，2019（11）：59。也有人认为，符号意识是个体在感知、理解、運用数学符号时所表现出的一种主动反应，或是面对符号时产生的一种复杂、多维的感觉，将符号意识视为个体对符号的感受和领悟能力。朱立明，胡洪强，马云鹏.国内外数学符号意识研究：回顾与展望[J].天津师范大学学报（基础教育版），2017（2）：72。这种“感悟说”将符号意识理解为对符号的感悟。“悟”往往与潜意识相关，而潜意识指向的是思维的感觉，而不是思维本身。

对于符号意识的理解，既要从符号的角度出发，也应强调对意识的理解，而“数学符号意识”则应该在此基础上突出数学的本质。我们知道符号是一种标记，比如文字是记录语言的符号，因此符号是对某种对象的标记、反映。美国符号学家皮尔士认为，符号包含符号（symbol）、对象（object）和解释（interpretation）三个主题，对象是现实事物或另一个表征符号，而符号与对象的联系基于符号使用者头脑中产生的解释。查尔斯·S.皮尔士.皮尔士论符号[M].徐鹏，译.上海：上海译文出版社，2017：113。这样的解读强调了人在符号与对象之间所起到的中介作用，同时也强调了符号是对某种意识对象的意义标识。在心理学中，将意识理解为个体的大脑对于客观物质世界的反映，是感觉、思维等各种心理过程的总和。符号意识一般译为symbol sense，这里的意识（sense）可包括知觉、感觉、思维、想象等多种活动。而从数学的角度看，数学（知识、内容）本身就由大量的符号组成的，数学符号是人们在数学领域进行表达、运算、推理、证明、问题解决的核心工具。符号成就了数学，推动着数学科学的发展。

再结合小学数学、小学生思维等的具体特点，我们可以将小学阶段的数学符号意识理解为学生在符号表达、符号关系、符号运算、符号推理等方面的感受、体会、理解、运用等反映。符号意识是一种内外相结合的综合素养，但可以通过学生某些外在的行为加以体现。

（二） “符号意识”如何发展

小学阶段主要涉及元素符号、运算符号、关系符号、几何符号、结合符号、计量单位符号、特殊符号、性质符号、约定符号等多种类型的符号。对于小学生符号意识的培养，要注意引导学生理解符号的含义、感受符号的便利，体会到符号是数学的语言，从而主动在数学中用符号、在生活中用符号。

1. 由直观到抽象，理解符号的内涵。

有研究强调，学生符号意识的培养首先要明确符号的内涵，理解符号的意义。教师在教学中不能片面地强调学生对数学符号的记忆，而要注重引导学生对数学符号的意义与本质的理解。通过教学，学生应能够理解数学符号所表达的含义，以及如何运用数学符号表达内容、数量关系、推理证明等。

符号是脱离了种种具体实际所形成的一种高度概括的语言，具有抽象性。要促使学生，尤其是小学生理解抽象的符号，应当将这种抽象置于一定的情境中，使其直观化、具体化、易理解化，促进学生由个别到一般地理解，完成符号的抽象。

“数的认识”是“数与代数”领域的基础内容，是学生学习“数与代数”领域其他内容的前提。数实际上就是一种元素符号。数概念的形成是经过一系列由具体到抽象的过程，舍弃其他一切非数量关系的内容后，只保留数量的关系所抽象的结果。李艳琴，宋乃庆.小学低段数学符号意识的培养策略研究[J].数学教育学报，2016（5）：28。在小学数学教学中引导学生认识数、理解元素符号，要尤其注重从直观到抽象、从具体到概括的过程，逐步引导学生在不同的情境中理解数的含义、本质。

比如，1—10的认识，教师在教学中要赋予1—10各数具体的情境和具体的含义，帮助学生来抽象其所表示的数的含义（如提供1个太阳、2只小鸟、3棵大树、4朵鲜花等具体情境），同时鼓励学生自己用1—10各数来描述生活中的一些物品。这便是一个由直观到抽象、由具体到概括的理解数字符号的过程，能够加深学生对1、2、3等数字的本质内涵的理解。

再如，在乘法分配律等运算律的教学中，学生结合具体的问题情境和计算得出7×（4+5）=7×4+7×5后，教师引导学生观察发现等式的特点——等号两边的数字相同，但位置和出现次数不同，且等号两边的计算结果相同，再启发学生尽可能多地列举出具有一定内涵的同类型等式，由此抽象出一般化表达式a×（b+c）=a×b+a×c。这样由具体到抽象、由个别到一般的过程更利于学生理解运算律的本质。

2. 注重比较，感受符号的简洁便利。

在小学数学教学中，教师要引导学生在对比中感受符号的简洁、便利，启发学生主动接受符号，体会符号在数学学习中的必要性，才能促使学生自觉选用恰当的符号表示。基于数学本身的特点，学生在数学学习的过程中往往要经历从个别到一般的抽象过程，这种数学活动本身就利于学生比较体会数学符号的概括性、简洁性。高晓娟.发展符号意识，提升数学素养[J].天津教育，2020（6）：185。

比如，教学苏教版小学数学一年级上册《数一数》时，教师引导学生经历由画出实际物品，到用点表示，再到后续学习中的用数字表示的过程。这样，学生能够在逐步数学符号化的过程中，主动比较、体会、理解数学符号的概括性。

此外，在各种运算律的教学中，也可带领学生经历具有比较性的学习活动。如，学生通过对多个等式的观察发现乘法交换律的特点后，可鼓励学生用自己的语言总结其特点，即“两个数相乘，交换因数的位置，它们的积不变”;在文字表达的基础上，让学生用符号进行表达，从而引出a×b=b×a，促使学生在比较中感受符号的简洁、便利。

需要注意的是，教师在教学过程中不要急于将抽象的、符号化的内容呈现给学生——缺乏过程性、体验性的数学学习，既不利于学生对所学知识、符号的理解，也不利于学生在比较中感受符号的简洁性。

3. 在运用中体会符号的优势。

熊建平等人在相关研究中强调，符号意识的培养应落实在问题解决过程中，引导学生在具体情境中用符号抽象概括数量关系、变化规律，在解决问题的过程中，理解符号所表达的数量关系、变化规律，通过不同符号表达形式之间的转化，感受数学符号的优势。熊建平，余芳芳，张红，等.例谈初中符号意识教学[J].湖州师范学院学报，2019（6）：103。同时，运用符号表示数、数量关系和变化规律也是《课标》对学生符号意识发展所提出的要求，即符号的运用既是措施，也是目的。因此，在小学数学教学中，教师应有意识地组织学生开展运用符号的学习活动。

比如，教学“含有小括号的混合运算”时，教師不应直接告知学生在含有小括号的混合运算中要先算小括号里的，而要引导学生在解决问题的过程中产生对小括号的需求，以及对小括号作用的深刻理解。教师可以出示问题情境：“小明用50元买了一个10元的文具盒，用剩下的钱去买5元每本的笔记本，可以买几本？”让学生先分步计算，得到50-10=40（元），40÷5=8（本），并说清楚每一步的含义。在此基础上，鼓励学生列综合算式。学生可能会列出50-10÷5，教师引导学生分析：若按照先乘除后加减的运算规则进行计算，则结果与分步计算的结果不一样;若按照题意先算50-10，则不符合运算规则。此时，学生自然产生添加某种符号的需求，小括号的出现顺理成章。

三、 “运算能力”及其发展

（一） 对“运算能力”的解读

依据《课标》，运算能力主要是指能够根据法则和运算律正确地进行运算的能力。培养运算能力有助于学生理解运算的算理，寻求合理简洁的运算途径解决问题。中华人民共和国教育部.义务教育数学课程标准（2011年版）[S].北京：北京师范大学出版社，2012：6。崔志翔博士在分析义务教育阶段的数学核心素养时用“数学运算”代替了“运算能力”，认为数学运算是指理解数、符号等运算对象，掌握基本运算规律与法则，选择合理简洁的运算程序与方法，正确求得运算结果。崔志翔，杨作东.义务教育阶段一个数学核心素养的评价框架[J].数学教育学报，2021（5）：49。这样的理解，强调了算法、运算律、算法选择、运算技能，但没有强调算理，忽视了运算的内在本质，容易让运算教学重结果轻过程、重记忆轻理解。黄毕年在解读运算能力时，强调了算理与算法的并存，同时从数学的本质及特点出发，得出了“运算能力是遵循思维活动的路径，对运算关系进行归纳、类比、演绎，作出数学推理的能力”黄毕年.遵循路径依据关系强化推理——对运算能力的本质性认识[J].福建教育，2020（49）：41。这样的界定。此种理解从运算中的思维活动出发，强调个体对数与数之间相加等特定数学关系的联结、比较、推理的过程。笔者以为，运算能力的发展能够帮助学生选择算法，反过来，合理选择运算方法、途径也应该成为学生运算能力发展的表现之一。为了发展学生的运算能力，应该引导学生在尝试计算的过程中理解运算的道理（算理），在理解算理的基础上，概括、总结、简化出算法。运算能力的发展是个体基于对数、符号等元素的认识，从理解算理、掌握算法到选择运算类型、推理运用的全过程。

（二） “运算能力”如何发展

1. 基于情境，理解算理，掌握算法。

所谓算理，即运算的道理。按照知识分类学理论，解决的是“为什么”的问题。而算法，即运算的方法，解决的是“怎么做”的问题。运算是元素符号、运算符号之间的一种相互作用，充分体现了数学的抽象性。结合具体的情境，将符号赋予一定的含义，是较好地帮助学生理解算理的方法，学生也更容易在具体的情境中解释为什么。

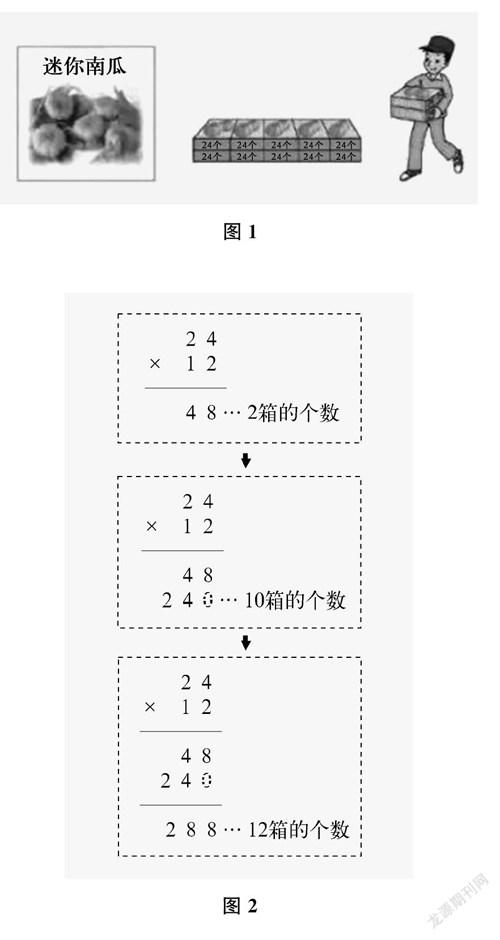
比如，苏教版小学三年级下册《两位数乘两位数的竖式计算》一课，教材创设了“幼儿园购进12箱迷你南瓜，每箱24个。一共有多少个？”的问题情境，并且通过直观的主题图（见图1），启发学生产生先算10箱和2箱各有多少个南瓜，再将它们相加算得总和的拆分计算方法。这同时也为学生理解竖式计算的运算顺序做了铺垫。教学中要基于24×2=48（个），24×10=240（个），240+48=288（个）的拆分计算，引导学生理解24×12竖式计算的运算顺序。由图2可见，竖式计算的运算顺序和含义同拆分计算相同，教师可以基于学生拆分计算时每步计算的含义，提问学生在竖式计算的过程中每一步分别计算的是什么。由此，引导学生认识到，竖式计算同样是先算2箱的个数，再算10箱的个数，最后相加，帮助学生理解运算的过程及道理，掌握竖式计算的方法。

2. 推理论证，“发现”算法。

运算教学不能只是让学生记住算法，还要让学生“发现”算法。小学数学教学中，教师应引导学生经历简单的推理猜想、举例验证、归纳总结的过程，促使学生“发现”算法。

比如，在学生理解了0.8×3=2.4、2.35×3=7.05等小数乘整数算式运算道理的基础上，教师可以引导学生观察比较“乘数中小数的位数与乘积中小数的位数之间的关系”。学生可以初步归纳出规律“乘数中总共有几位小数，乘积中就有几位小数”。对此，教师要鼓励学生大胆猜想：是不是所有的小数乘整数的算式，都是乘数中总共有几位小数，乘积中就有几位小数？让学生先猜想4.76×12、2.8×53、103×0.25等算式乘积中的小数位数，再通過计算器计算加以验证，从而“发现”算法。

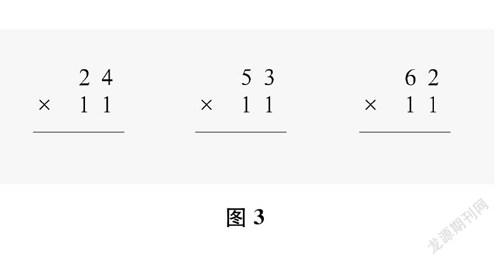
再如，在“有趣的乘法计算”教学中，教师首先引导学生观察比较，发现算式（见图3）本身的特点“都是两位数乘11”，然后鼓励学生计算，将乘积与乘数进行比较，初步发现乘积的规律“积的个位与第一个乘数的个位相同，积的百位与第一个乘数的十位相同，积的十位为第一个乘数个位与十位上的数相加之和”。由此，鼓励学生猜想是不是所有的两位数乘11的计算结果都具有这样的规律，并让学生多举一些同类型的算式进行计算验证（注意乘数个位与十位上的数相加之和大于等于十的情况），从而得到“两头一拉，中间相加，满十进一”的算法规律。

3. 培养估算意识。

估算主要是指通过数量的近似凑整，获得计算的大致结果或范围。虽然估算的计算结果不够精确，但计算过程却十分便捷。它不仅在生活中有广泛的应用（很多时候并不需要精确结果），而且在数学中也有重要的作用（如试商、比大小、检验结果等）;同时，它也是培养运算能力以及思维灵活性的重要途径与方法。在估算教学中，帮助学生掌握估算的方法不难（基本的思路就是近似凑整），难的是培养学生的估算意识和习惯。因为计算或解决问题时，大多数学生的第一反应是精确算出结果。归根结底，这和教材的内容设置有关：小学数学教材中，精确计算占了95%以上，估算只占不到5%。长期接触和训练精确计算，学生自然缺失了估算的意识和习惯。因此，教师应该从学生的现实生活经验出发，创设估算情境，提供估算的机会，让学生在真实的经历体验中，培养估算意识和习惯，提升估算能力。

比如，教师通过呈现“小明去商店购买牛奶、面包、鸡蛋，牛奶为1.5元，鸡蛋1.29元，面包1.44元，什么情况下使用估算比精算更有意义？A. 当收银员将每种食品的价格输入收银机时;B. 当小明被告知应付多少钱时;C. 当收银员计算小明所付的费用时;D. 当小明试图确认5元是否够用时”的问题情境，引导学生理解估算的意义与使用。

再如，教师设置“西瓜每箱48元，买4箱，带200元够不够？”的问题情境，引导学生理解可以将48看作与之相接近的整十数50进行计算，50×4=200，而48<50，所以48×4<200，因此带200元够用。通过这样的过程经历，帮助学生掌握估算的方法，感受估算的便捷与价值，树立运用估算的意识。（殷如意，宿迁学院教育系。主要研究方向：小学数学教育教学。）