合理分类 理清概念
王见新




[摘 要] 概念学习是小学数学学习过程中的一项重要内容,其分类与层次对构建学生的概念学习系统有着重要的意义。概念分类是数学思想中的一个分支,它既是构建学生数学概念的基础,又是加深学生理解数学概念的途径。数学学习的过程就是用数学概念不断进行分析、比较、概括、综合、推理和判断的过程。文章从概念形成、概念同化、概念形成和概念同化相结合三个方面具体阐述概念分类的思想。
[关键词] 数学概念;概念分类;概念同化
数学概念泛指一种思维形式,指人脑对客观对象的空间形式与数量关系本质属性的反映,一般以公式、法则、或定理的方式呈现。理解并合理使用数学概念是学好数学这门学科的基础与前提。概念分类是概念学习的重要载体,教师不可能将所有的数学现象提供给学生,而是提供一些不同类的数学材料,组织学生对这些材料进行分类总结,推理出同类数学概念 [1]。奥苏伯尔(D.P.AuSubel)认为数学概念的形式有概念形成和概念同化两种形式。教师可根据概念的形式,引导学生充分感悟概念分类的过程,提高数学思想。
一、实操分类,感知概念形成
学生大脑中原有的数学概念与新概念之间达到平衡的状态是数学概念形成的原始动力,概念形成的过程就是学生获得同类事物共同属性的过程。教师可引导学生通过实际操作,让学生在经历中感知数学现象的抽象、概括、分类,从而发展学生的数学空间概念并感知概念形成的具体过程。概念形成过程一般经历以下几个步骤:辨别,学习者根据实际情况找出数学材料的基本属性;分类,将数学材料中同一属性的归为一类;抽象,剔除材料的非本质属性,用语言提炼其本质属性;检验,对比其他数学材料是否也存在这种属性;概括,文字表达这种属性;形式化,用字母或数学符号表达,概念形成。整个过程环环相扣,缺一不可。
案例1:“平年与闰年”的教学。
在学生初步认识年、月、日后,让学生通过各种方式统计近五年期间每个月的天数,记录下来。
师:同学们都对近五年期间每个月的天数进行了统计,现在请大家观察自己记录的数据,找找每个月天数的规律。
生1:我发现大部分月份都是30天或31天。
生2:我发现每年的2月份天数不固定,其他相同月份是固定的,比如每年的3月份都是31天。
生3:对的,2020年的2月份是29天,比2019年多1天。
师:同学们观察得都很仔细,那我们就单独观察一下2月份的天数,大家说说你的发现。
生4:2020年和2016年的2月份都是29天,2017年、2018年、2019年的2月份都是28天。
师:很好,今天我们要学习的知识就是“平年与闰年”的概念,2月份有29天的年份,我们称其为闰年;2月份有28天的年份,我们称其为平年。我们再观察闰年年份的数字与平年年份的数字有什么区别。(学生交流讨论)
生5:2016年和2020年这两个数都是4的倍数,而2017年、2018年、2019年的数都不是4的倍数。
……
教师选择让学生观察近五年每月的天数,目的在于引导学生通过观察与比较迅速找到不同年份中每个月天数的异同属性,学生寻找到2月份以外每个月天数的固定规律后,再针对2月份这个特殊月份进一步比较分析,从而获得闰年和平年的本质。这种通过实际操作分类逐渐形成的概念,不仅培养了学生观察分类标准的严谨性,还让学生充分感知了平年和闰年概念形成的过程。学生通过亲自参与分类获得的数学概念比直接诵读获得的数学概念要牢固稳定得多。
二、衍生概念,感知概念同化
概念同化一般指利用学生认知中原有的概念,用定义的方式提示新概念的主要特征,让学生获得新概念的方式。概念同化多用于衍生概念教学中,以衍生概念的原概念作為课堂教学的起点,通过激活学生认知结构中原概念知识的经验而同化出新概念。新概念是否得到充分的同化,主要取决于学习者原有概念与新概念是否能达到平衡的状态 [2]。因此,教师引导学生获得概念同化的关键任务就是从实际情况出发,使用观察、操作、分类与分析等方法,协助学生达成新概念与原概念的平衡。
案例2:“认识方程”的教学。
教师在白板上展示以下8道式子,要求学生分组讨论这8道式子的分类方法。
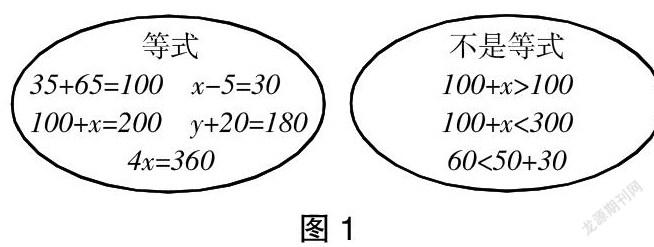
35+65=100 100+x>100
100+x=200 100+x<300
x-5=30 y+20=180
60<50+30 4x=360
一部分学生将式子中有“=”号的分类在一起,有“<”或“>”号的分类在一起(见图1):
还有一部分学生将含有字母的式子归为一类,没有字母的式子归为一类(见图2):
教师鼓励学生从图1和图2的分类方式寻找异同点,经过分组讨论后得出下图(见图3):
教师在三张图形的基础上揭示方程的概念。其实方程是等式衍生出来的新概念,学生的认知结构中原有等式的概念,经过教师的引导由浅入深地层层递进,衍生出新概念——方程。图1根据式子是否含有“=”号进行分类,图2根据式子是否含有字母进行分类,再对这两种分类结果进行观察比较,寻找出异同点,学生能清晰地认识到其中的关系——有些式子含有字母的同时又是等式,方程的概念也昭然揭晓。这是概念同化的过程,是学生根据式子的分类逐层揭晓新概念的本质,明确等式与方程的区别与联系,在大脑中构建新的认知。
三、两者结合,形成概念系统
构建良好的概念系统,需将概念形成和概念同化的方法结合在一起使用。学生在两种方法结合的过程中体会概念之间的关系,可用下图(见图4)表示:
根据概念系统形成的图示可见:概念系统的形成首先是学生根据实际操作或实例进行观察、分析、分类,总结出概念的本质;然后在概念形成的基础上,通过观察和分类将大脑中原有的概念衍生出新概念;再根据概念之间的内部联系,逐渐形成良好的概念系统 [3]。
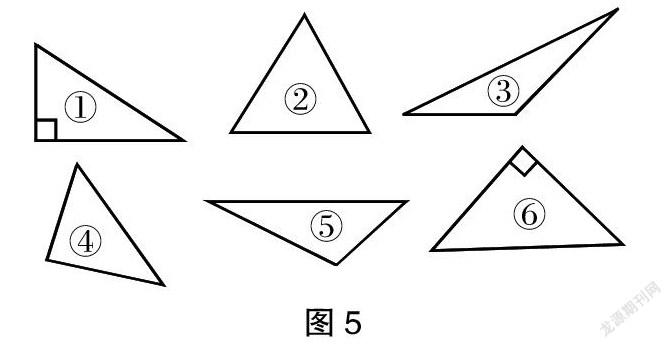
例如,“认识三角形”的教学,展示一组三角形(见图5)。
师:观察图5,其中图①、图②的三个角分别是什么角?
生:图①有一个直角、两个锐角;图②有三个锐角。
师:我们来量一量看(在白板上演示量角器的测量过程),可见这位同学的回答是正确的。大家再观察一下其他的三角形,是不是所有的三角形都是由直角或锐角组成的呢?
生:图③和图⑤里面有钝角。
师:这位同学观察得很仔细,现在大家来填写这张表格(表1)。
学生根据表格的结果进行三角形分类如下:
(1)有直角的是图①和图⑥,没有直角的是图②、图③、图④、图⑤;
(2)有钝角的是图③和图⑤,其他四幅图形都没有钝角;
(3)有三个锐角的是图②和图④,有两个锐角的是图①、图③、图⑤、图⑥;
(4)三个角都是锐角的是图②和图④,有一个直角、两个锐角的是图①和图⑥,有一个钝角、两个锐角的是图③和图⑤。
学生在交流过程中分别阐述了分类的理由,各种角度分类,显示出层次感与条理性,并从分类中引出锐角三角形、钝角三角形和直角三角形的概念。这是概念形成和概念同化相结合的过程,学生也由此对三角形产生了完整的认识,形成系统概念。
综上所述,构建数学概念需学生经历比较、分类、讨论、总结的过程。学生经历概念形成和概念同化过程中的分类,逐渐积累经验,感悟分类是概念系统形成的重要载体。若遇到层次繁多而复杂的情况,教师可引导学生从各个角度确定分类标准,化难为易,不漏不重地归类总结,解决问题,帮助学生构建新的概念体系。
参考文献:
[1] 邱呈玲,宋庆福. 中学数学概念教学的策略研究[J]. 荆楚学刊, 2003(06).
[2] 崔友花,李庆民. 将概念教学进行到底——谈数学教学中的概念教学[J]. 网络科技时代,2007(16).
[3] 徐正洲. 在概念建构中感悟分类思想——以《三角形按角分类》的教学为例[J]. 小学教学研究,2018(25).

