小学数学教材中“思考题”教学策略例谈

胡剑

[摘  要] 苏教版小学数学教材中适当地编排了一些“思考题”，这些思考题作为课程资源，为教师发展学生的智能和培养学生的学习兴趣， 提供了很好的、可利用的材料。随着素质教育的不断深入，培养学生会思考、会学习，这些思考题起到了一定的作用。文章立足于教材中的三道思考题，寻求有效的教学策略，让思考题“亲民”，让大多数学生跳一跳能摘到“果子”。

[关键词] 覆盖面;一般到特殊;解题策略;摘果子

苏教版教材的练习设计有一个特点，会时不时给学生“加料”，在单元末尾来一道“菜”，用方框框起来，并标有底色。学生习惯上叫这些 “方框题”为“附加题”或者“思考题”，遇到这种题目，聪明孩子摩拳擦掌跃跃欲试，一般的孩子则畏首畏尾无从落笔。2011版《小学数学新课程标准》明确要求，“人人能获得良好的数学教育，不同的人在数学上得到不同的发展 [1]”，“人人”是就覆盖面而言，良好的数学教育是应该面向全体学生的，同时也要承认学生存在差异，“不同的人”有不同的发展目标。教材提供的思考题，既要让全体学生得到发展，又要帮助学生建立自己的数学现实和数学学习的直觉，学会运用数学的思维方式进行思考。

在苏教版数学四下教材里，一共安排了三道思考题，第三单元“三位数乘两位数”安排了一题，第六单元“运算律”安排了两题，这三道题都是放在该单元的最后一页。这册教材安排的这3题，我们需要教会学生些什么呢？

一、寻求解决问题的方法——从一般到特殊

【例1】 苏教版小学数学教材四下37页：

这道题的出现，使得难度一下子拔高了许多，学生的错误率一直居高不下。教师使出浑身解数，各种奇招，希望能把准确率提高上去。题目中4、3、2、1、0五个数字中含有0，有一定的特殊性，“遇到特殊问题，想想它的一般情形是什么;掌握了一个解个别问题的方法，想想它能不能用来解别的更一般的问题：这就是学数学时应当常常注意运用的一种思考方法 [2]”，我们就从一般情况入手，先去掉特殊数字“0”，按下列情形逐步进行探究：

情形一：把4、3、2、1放入□□×□□乘积最大是多少，最小是多少？

两个数的首位应该分别先放4和3，变成了4□×3□，接下来两个数的第二位分别放2和1，只有两种情况：42×31和41×32，筆算可以很容易算出，42×31=1302，41×32=1312，2放在3的后面乘积更大。还可以从算理上得到验证：4□×3□，不管后面怎么放，两个数的首位都是四十几乘三十几得1200多一些，可以不去考虑。如果较大数2放在首位大数4的后面，那么2×3□得60多一些，而如果放在首位小数3后面，则是2×4□得80多，很明显，较大数2放在首位较小数3后面，即41×32积会大。同理求最小，先取最小的两个数1和2作为两个数的首位，再取3和4，要使得积小，3放大数2后面，4放小数1后面，得14×23=322是最小。

情形二：把5、4、3、2、1放入□□□×□□乘积最大是多少？最小是多少？

先取5和4作两个数的首位，再取3和2，3应该放在小数4后面，2放在大数5的后面，得到52×43是最大的，1放大数52就是1×43=43，放小数43这边就是1×52=52，显然结论和前面一样，应该放在小数这边积会更大些，即52×431=22412最大。积要最小，最后一个5放大数23后面，14×235=3290是最小的。

归纳总结：要想得到积最大，先选择最大的两个数字确定首位，再选次大的，大的跟在小的后面，小的跟在大的后面;要想得到积最小，先选择最小的两个数字确定首位，再选次小的，大的跟在大的后面，小的跟在小的后面。我们可以再试一些，比如1、2、4、7、9;或者4、6、7、8、9来验证思路的准确性。为了便于记忆，编口诀“积最大，大跟小，小跟大;积最小，大跟大，小跟小”。

情形三：处理有0的特殊情况。回到教材上“思维题”，对于4、3、2、1、0，积最大没有影响，可以照搬口诀完成前4个数字，得到41×32最大，最后一位0可以放在任意数的末尾，410×32或41×320。积最小，由于0不能作首位，先确定最小的两位1和2作为两个数的首位，接下来是0和3，“小跟小”，0在1的后面，3在2的后面，最后一位是4，4没有跟谁比，看作“大”的数， “大跟大”，更在23的后面。

积最大：41×320=13120;

积最小：10×234=2340。

再来看看解决这个问题的另外一种方法——“un笔顺法”。

仍然从一般情况来思考，先考虑没有0的情况。

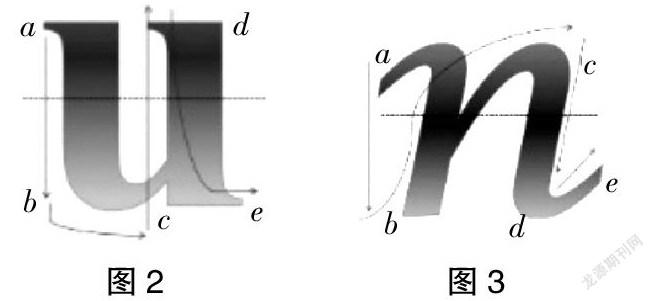
求最大：把a、b、c、d、e五个数字从大到小排列，分别摆在字母“u”的五个位置（如图2），这五个位置的摆位是以书写字母“u”的笔顺来定位的，乘积最大是：ad×bce。如果是数字1、2、3、4、5，用这个方法得到乘积最大的算式是：52×431=22412。

求最小：把a、b、c、d、e五个数字从小到大排列，分别摆在字母“n”的五个位置（如图3），这五个位置的摆位是以书写字母“n”的笔顺来定位的，乘积最小是：ac×bde。如果是数字1、2、3、4、5，用这个方法得到乘积最小的算式是：13×245=3185。

再考虑有0的情况：当这个五个数字中有一个是0时，求积最大没有问题，本身0就是5个数字中最小的，按43210顺序排，0排在最后，可以用“u”来做，很容易得到积最大的算式是41×320=13120;但求积最小时，按01234顺序排，0不能排在首位，这里“0”的位置被安排在固定位置“C”位，剩下的4个数字从小到大排列在a、b、d、e的位置，得到积最小的算式10×234=2340。

这两种方法，有两个共同的特点，一是都从一般到特殊来研究，得出一般性的结论再来考虑特殊情况下需要打什么“补丁”，最后又回到一般情况来解决问题，“由一般到特殊的学习路径，且突出一般方法内涵本质的理解，更有利于帮助学生形成策略性知识，发展解决问题的策略水平 [3]”;二是都有一个既定的“程式”需要学生来记忆，后者需要记住图——“un笔顺法”，前者需要记住一句话——“口诀”，学好数学，“记功”功不可没，各种运算律、各种公式等等，是必须要记住的。但前者应该更值得提倡，即使忘记了“口诀”，也可以从算理上重新求得，并且可以扩展到三位数乘三位数，三位数乘四位数，四位数乘四位数……，都是适用的，这符合“新课标”对第二学段倡导的“发展合情推理能力，能进行有条理的思考”的目标要求。

二、寻求练习的层次性——从最基础出发

【例2】 苏教版小学数学四下教材67页：

在第六单元“运算律”的最后，安排了这样两道简算题，无形中把乘法分配律的运用提高了许多。这个单元有三个运算律，乘法分配律是重点，也是一个难点，学生需要会运用乘法分配律来进行简算，教材给出的配套巩固练习，都是基于乘法分配律的“模型”来设计的，（a+b）×c=a×c+b×c这个“模型”是学生必须要掌握的，这是利用运算律解决其他较难题目的基本保证，“学生学习能力不同，导致对知识的理解、应用能力也有所不同，所以，课堂练习的设计要有层次、有变化、有发展，适合班级每个学生的要求 [4]”，从而整体提高每个学生的学习能力。

第一层次练习，基本题，保证全体学生“吃得饱”：

68×35+68×65;36×42+42×64;75×25+25×25。

这类习题要求人人都掌握，直接套用乘法分配律“模型”，找到相对应的a、b、c位置进行解答。68×35+68×65=68×（35+65）;36×42+42×64=42×（36+64）;75×25+25×25=25×（75+25）。

第二层次練习，变形题，绝大多数学生“吃得好”：

45×99+45;45×101;63×99。

这类习题需要对题目进行简单的“加工”，制造出乘法分配律的“模型”，变成第一层次类型的题。45×99+45=45×99+45×1;45×101=45×（100+1）;63×99=63×（100-1）。

第三层次练习，较难题，学有余力的学生“够得着”：

75×280+750×72;66×27+33×46。

这类习题需要借助“积不变的规律”对原题进行变换，改造出乘法分配律的“模型”：75×280+750×72，把75扩大10倍，280缩小10倍得到算式750×28+750×72;66×27+33×46，把66缩小2倍，27扩大2倍得到算式33×54+33×46。课本中的例2属于这一类，360是36的10倍，999是111的9倍，相信大家会做了。

第四层次练习，竞赛题，少数学生可以顶顶脚跟去“摸一摸”：

280×234+1110×576+6540×28。

这类习题是多种知识的相互渗透，要从表面上杂乱无章的数来构造出乘法分配律的模型。很显然，因数28和280是一个突破口，先把280×234+6540×28改造成28×2340+6540×28，得到28×（2340+6540）=28×8880，这题就变成28×8880+1110×576，发现8880是1110的8倍，利用“积不变的规律”再构造成28×8880+8880×72，再次变成了基本题。

上面四个层次的练习，不管是哪一层次，最后都要回到本源上来，这个本源就是教学大纲要求的“基础知识”和“基本技能”，乘法分配律在初中阶段是一个寻求公因数的过程，同时也是一个合并同类项的过程，在小学阶段，是建立乘法分配律模型（a+b）×c=a×c+b×c的过程，是寻找或构造相同数“c”的过程，遵循认知规律，在思考的过程中，要引导学生用一双“慧眼”去捕捉算式中各个因数的内在联系，做出适当变换，转化成基本题。

三、寻求解题的高效性——从“整体”来思考

【例3】 苏教版小学数学四下教材71页：

这是一道行程问题里的“相遇问题”。行程问题的一个最基本数量关系是：速度×时间=路程，扩展到相遇问题，这个关系式变为“速度和×相遇时间=相遇路程”。已知条件中“速度和”可以求到，相遇时间也有，现在“合”在一起来整体思考，（65+70）×5=675米，求得的是什么呢？当然是相遇路程，这个相遇路程是桥长吗？这个时候就要分开来考虑了。可以配合线段图来分析（如图6）：

图中可以看出，从出发到第二次相遇，小华走了一个桥长多一些，小明也走了一个全程多一些，各自的多一些，合起来也是一个桥长，两个人一共走了3个桥长。通过前面的“先整体来思考，再分开来思考”，发现“速度和×相遇时间”原来就是3个全程，问题得到解决：（65+70）×5÷3=225米。

我们可以继续深究：如果两个人经过5分钟是第三次相遇，结果又是怎么样呢？先整体思考，“速度和×时间”先求得两人行的总路程，这个思路是没错的，需要思考的是一共行了几个全程（桥长），分开来分析各自行的过程，不难发现小华行了2个全程多一点，小明也行了2个全程多一点，一共行了5个全程。（65+70）×5÷5=135米。第四次相遇呢？第五次相遇呢？都可以按照这个方法来解决问题。

可以把下面一题引导学生来“跳一跳”，看看能不能“摸得着”：

植树节到来，甲、乙、丙三个小队去植树，都领了同样多的树苗。这批树苗甲队植完需要10小时，乙队植完要12小时，丙队植完要15小时。同时开工的时候丙小队的树苗给另外班级了，丙队决定帮甲、乙两队一起完成，丙队开始帮甲队一起，中途又转向帮乙队，最后这两批树苗同时植完。问丙小队帮了甲小队几小时？

先“合”，整体来思考，把甲乙两队的工作总量都看作单位“1”，总工作量就是“2”了，由于这些树苗是三个小队共同完成的，同时开始，同时结束。先不考虑中间状态，根据“工作总量÷工作效率=工作时间”可以求出这些树苗一共需要几小时植完。

列式：2÷++=8（小时）。

再“分”，思考丙先帮甲几小时。这道题就变成：甲、丙共同植一批树苗，如果甲队单独植需要10小时，丙队单独植需要15小时。丙队因为要去帮乙队而离开了，结果8小时植完了这批树苗，问丙做了几小时后离开。甲8小时一直在做，做了×8，剩下的是丙帮甲做的，帮了几小时？

列式：1-×8÷=3（小时）。

先合再分，圆满地解决了这个问题。这里的“整体思维”起着至关重要的作用。解决问题本无定法，追求高效是解决数学问题的王道。

现今，对学生掌握数学知识的评价一般是7∶2∶1来分配的，基础知识（基本题）占70%，是教材例题的复制，这是立身之本，学生必须要掌握;20%是基础知识的延伸（中档题），大部分学生能够得分;而最后一成是比较难的，属于教材里的“思考题”行列，学生“差异化”的表现就集中在这里。我们教师所做的，就是要把这些思考题变得“亲民”些，让大多数学生能体验到成功的喜悦。于是，从前面分析整册教材安排的三道“思考题”之后，有了以下三点思考：

思考一：“跳一跳”怎么跳。抓基础是王道。我们一直鼓励学生要有“探险”的精神，遇到难题要勇敢地去尝试，但如果根基不牢，注定会碰得头破血流。在例1中对求最大乘积与最小乘积中，表面上是只要去记住“口诀”，实际上“口诀”的背后是三位数乘两位数的算理作支撑;例2中首先要对乘法分配律的“模型”熟悉，左边到右边、右边到左边的灵活切换，还有“数的分与合”“积不变的规律”应用其中;例3中“速度、路程、時间”到“速度和、相遇路程、相遇时间”的数量关系转变等。

思考二：“摘果子”怎么摘。“果子”很甜，摘之有“道”，怎么样能采摘到，就要看你能否找到有效的解题策略。例1中两种方法都很好，你是记“口诀”还是记“字母”，选择适合自己的;例2中乘法分配律你能到达哪一层次，没关系，一步一步来，从最基础的开始，总会找到突破口，公式（a+b）×c=a×c+b×c的那个“c”位一定在某个地方等你;例3中学会“整体”看世界，忽视繁杂的中间环节，前面豁然开朗。

思考三：“助攻”怎么助。练习设计很重要。可以设计多解题，来训练学生思维的变通性;可以设计多变题（或多问题），训练学生思维的多向性;可以设计开放式习题，训练学生思维的广阔性;可以设计层次性练习，训练学生思维的有序性。当然，我们教师在“教学思考题时要引导学生通过比较、思考、讨论等方式，努力寻找解决问题的突破口和解题思路，使大多数学生都能体会到解决问题的乐趣，从而促进学生主动学习与发展 [5]”。

参考文献：

[1]  中华人民共和国教育部. 义务教育数学课程标准[M]. 北京：北京师范大学出版社，2012.

[2]  张景中. 数学家的眼光（典藏版）[M]. 北京：中国少年儿童出版社，2011.

[3]  费岭峰. 重设学路，突出数学学习的挑战性——小学数学由“一般”到“特殊”学习路径设计的实践与思考[J]. 小学教学研究，2018（2）.

[4]  黄娇艳. 指向核心素养的小学数学概念教学[J]. 教学与管理，2019（3）.

[5]  叶文生. 小学数学思考题有效教学的实践探索[J]. 小学教学参考，2006（z5）.