核心素养背景下中高考数学命题视角

钱德全 张晓蔚

(江苏省溧阳市光华高级中学，213300) (江苏省溧阳市永平小学，213333)

核心素养是学生应具备的、适应终身发展和社会发展需要的必备品格和关键能力.如何将教师日常工作的重点,引到培养提升学生的数学核心素养上来,这是当下的热门课题.

作为选拔性考试,区分度是首先要考虑的,但是,一味地追求区分度,命题难免会坠入难、偏、怪的圈子,使考试失去应有的效度.为此,必须加强命题研究,命制出有利于检测学生核心素养水平的考题,使题海战术失灵.切实做到:“科学设计考试内容,优化高考选拔功能,强化能力立意和素养导向,助力推动中学素质教育” .以“立德树人,服务选才,引导教学”[1]为导向的中高考数学卷的命制，可以从以下几个视角去思考.

视角1考卷应以“四基” 为主体.

中高考数学命题要增强基础性,考查学生的必备知识和关键能力.新课标将数学基础知识、基本技能、基本思想和基本活动经验称为“四基”.“四基”是学生在相应学段应该达到的基本要求,反映的是学生的基本数学素养.“四基”内容在教学大纲和课程标准中都有明确的规定.由“四基”产生的区分度合情合理,体现公平.

视角2考题要立足教材,源于教材而高于教材.

数学教材内容丰富,可以由数学概念命题,也可以由教材中的练习题命题.形象地说,概念好比一棵大树的种子,通过它生根发芽,生长成一棵枝繁叶茂的参天大树，数学体系庞大,任何一个数学分支莫非如此.概念是思维的细胞,概念不清,必然导致思维错误.在中学数学中,数学概念很多,对于现在还无法定义的一些概念,教学时可以淡化，但对于绝大多数概念来说,教学时不但不能淡化,反而应该加强,学生必须明确其内涵和外延.

1.依据基本概念命题

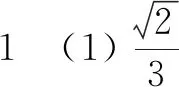
(2)(ln π)′=______(其中π为圆周率);

(3)“概率为0的事件是不可能事件”是______(填“真”或“假”)命题.

笔者曾做过一次测试,(1)，(2)，(3)的得分率依次为53.6%，45.3%，26.8%,区分度相当明显.典型错误如下：

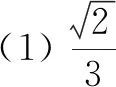
(3)“不可能事件的概率为0”是真命题,认为其逆命题也是真命题.其正解是:老教材有几何概型的教学内容,几何概型区别于古典概型的关键点就在基本事件的个数上,古典概型的基本事件个数是有限的,而几何概型的基本事件个数是无限的.从“有限”到“无限”,看似一字之差,但结果迥异.如问题:已知线段AB,在AB上任取一点C,求点C恰是AB的中点的概率.我们知道,该事件的概率为0.所以(3)应填“假”.

2.由教材中的练习题命题

例2观察下列图形,寻找对顶角(不含平角).(1)图1中共有______对对顶角;(2)图2中共有______对对顶角;(3) 图3中共有______对对顶角;(4)研究(1)～(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成多少对对顶角？(5)若有2 020条直线相交于一点,则可形成多少对对顶角？

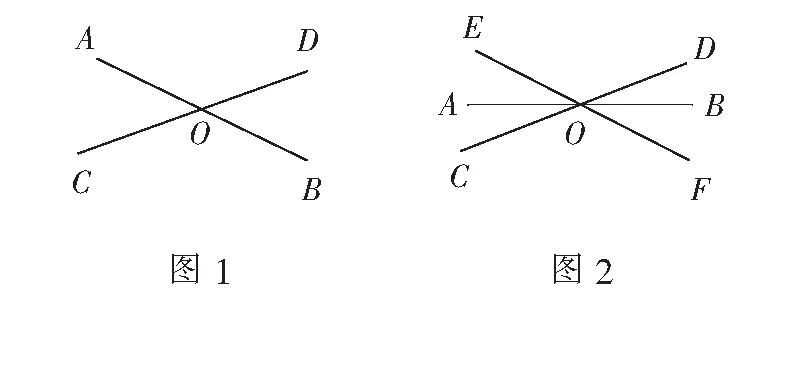
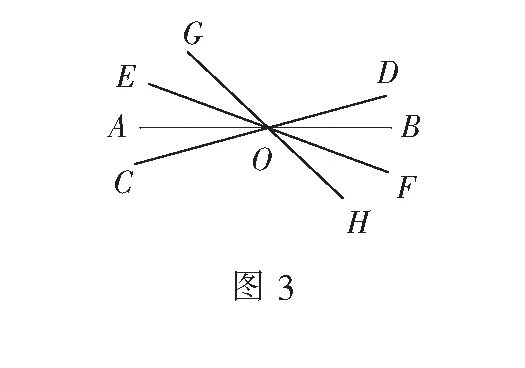
该题由教材中“对顶角”后的习题改编而成.题中五小问,由易及难,由具体到抽象,再由一般到特殊,有利于培养学生的观察能力、分析能力、归纳能力、演绎能力等多种能力;有利于学生数学核心素养的形成和发展.

中、高考命题一定要回归教材,依托教材编出新题,才能将各阶段的统考命题引入教材,教师就自然而然要钻研教材,而不是忙于为学生征订各种课外资料搞题海战.学生每门学科有多本资料在手,学业负担能不重吗?例2的前二问是教材中的原题,后三问由教师改编加深,将它作为中考题,对学生来说是公平的.

视角3考题要注意学科渗透.

数学作为工具性学科,与其它学科存在着广泛的联系.例如化学中大系数的化学反应方程式的配平,是学生的一大难点；物理学中对凸透镜成像结果的理解和记忆,同样是学习难点.

例3某同学在配平化学反应方程式FeS2+O2→Fe2O3+SO2时,采用了设未知数的方法:xFeS2+yO2=Fe2O3+zSO2,请你根据配平要求,运用数学方法,求出x，y，z,并写出配平后的化学方程式.

例4图4是凸透镜成像的光路图,已知BA⊥l,CD⊥l,EO⊥l,垂足分别为A，D，O，BE∥l,AF1=F1O=OF2=f,f为凸透镜的焦距,求证:CD=BA.

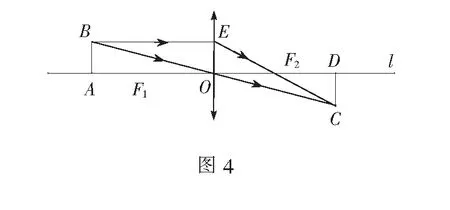
为了考查学生的数学建模能力,还可以将例4改为:实验发现:物体在凸透镜2倍焦距的位置,成既不放大也不缩小的倒立实像.请你解释“既不放大也不缩小”这一特点.学生要解决修改后的例4,必须依靠数学抽象、直观想象、数学建模等能力,将问题进行到修改前的状态,进而求解.

视角4考题应加强应用性,注重理论密切联系实际.

考题不能理论“空对空”,而要考查学生解决现实问题的能力，应用性主要体现考查学生运用所学知识解决实际问题的能力[4].

例5如图5,已知∠AOB,现仅有一把刻度尺(只可以画直线和测量长度),请你设计一种方案判断该角是否为直角,并说明理由.

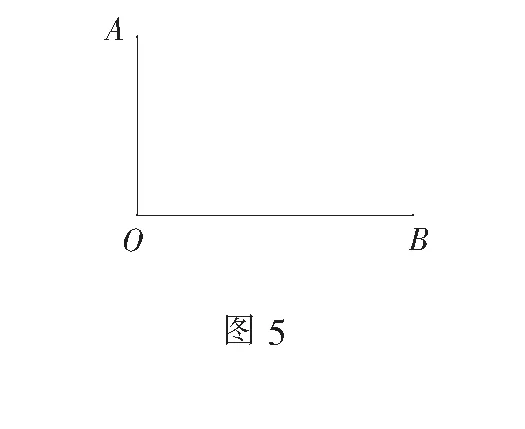
因为测量时会产生误差,所以该问题的答案并非“是”或“不是”,而是看学生设计的方案是否合理，旨在考查学生运用勾股定理的逆定理的能力.

视角5考题要注意学段知识的衔接.

同样一个问题,用后一学段的知识来解决可能非常容易,但是,用当前学段的知识来解决就比较棘手．这样的考题能检测学生的创新能力,同时,学生在后续学习中遇到类似问题时,会产生似曾相识的情感体验．

例6(1)已知a，b为实数,求证:a2+b2≥2ab.

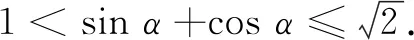
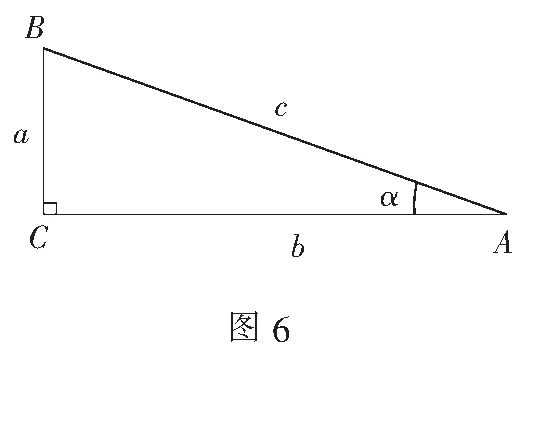
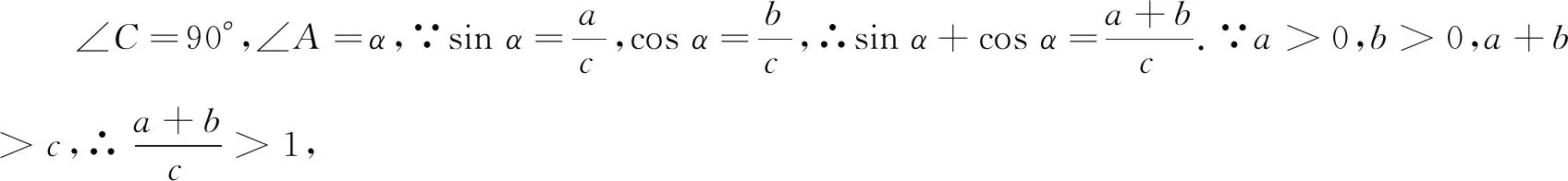
学段衔接题的命制和评分必须做到,高中学段的知识仅仅作为载体,考查学生驾驭现阶段知识和方法的能力,学生用高中学段的知识和方法来解答不得分,否则会导致高学段知识下沉,额外加重学生的课业负担.

视角6考题要有利于学生完善知识结构.

中、高考命题不能仅仅是为考而考,也要发挥它的育人功能.学生能用类比思想思考问题是素养的反映,但是,学生往往类比时不严谨，教师要善于发现这些关键点来命题.

例7我们知道,过椭圆外一点引椭圆的切线有2条,过椭圆上一点引椭圆的切线有1条,过椭圆内一点引椭圆的切线不存在.对抛物线和双曲线而言,我们作出以下规定:在同一平面内,以相应的曲线为边界,含焦点的区域为曲线内,不含焦点的区域为曲线外,整个平面分为三部分——曲线内、曲线上、曲线外.在同一平面内,过一点引抛物线和双曲线的切线,切线条数又是怎样?请你探索并得出结论.

直线与椭圆的相切问题,学生平时一定多次见过,可以说烂熟于心.但是,学生遇见了椭圆问题,是否会联想到抛物线和双曲线的问题,即发现和提出问题;联想到了抛物线和双曲线的问题,是否能科学地分析,合理地解决,即分析和解决问题.这些都能反映学生核心素养的不同层次.抛物线的切线情况与椭圆一致,双曲线的切线情况同中有异，比较复杂:点在双曲线内,不存在切线,即0条;点在双曲线上,有且只有1条切线;点在双曲线外且不在渐近线上,有且只有2条切线;点在双曲线渐近线上(中心除外),有且只有1条切线;点为双曲线的中心,不存在切线,即0条.此类问题不仅能检测学生的“四能”,而且有利于学生完善知识结构,使学生对圆锥曲线的切线问题有一个完整的认识,全面掌握其异同“数学学科应加强理性思维考查,体现创新性” .