高中对数函数易错题分析
刘 月
(江苏省滨海中学 224000)
对数函数是描述某些自然规律的一类重要函数,既是指数函数的反函数,也是高中乃至以后的数学学习中应用极为广泛的重要初等函数之一,是非常重要的.对数函数y=logax(a> 0且a≠ 1) 的图象有两个特征点,一定经过两个点(1,0)和(a,1).但同学们在解答此类函数题时因对函数的相关性质和定义不太熟悉,容易出现以下错误.现一一分析如下:
一、因忽略函数定义域易致错
例1函数f(x)与g(x)=2x互为反函数,则f(4x-x2)的单词递增区间为( ).
A.(- ∞,2] B.[2, + ∞) C.[2,4) D.(0,2)
解析由题意可知f(x)与g(x)=2x互为反函数,所以f(x)=log2x,f(4x-x2)=log2(4x-x2).由4x-x2>0,得0 例2函数y=log2(-x2+2x+3)的单调递减区间为( ). A.(-∞,3] B.[3,+∞) C.[1,3) D.(3,1) 解析函数的定义域为(-1,3),原函数可看作由y=log2u,u=-x2+2x+3复合而成,其中函数y=log2u是增函数,u=-x2+2x+3在区间[1,3)上是减函数,所以原函数的单调减区间为[1,3).故此题正确答案为C. 注:对函数的单调性问题,一定注意真数大于0的条件. 例3已知函数y=f(2x)的定义域为[-1,1],则函数y=f(log2x)的定义域为( ). 解析(1)由2x≤256,得x≤8.由log2x≥1,得x≥2,所以2≤x≤8. 注:复合函数的定义域容易被忽视,要特别注意对应关系,明确定义域的含义. 例5函数y=logax(a>0且a≠1)在[2,4]上的最大值与最小值的差是1,则a的值为多少? 解析(1)当a>1时,函数y=logax在[2,4]上是增函数,所以loga4-loga2=1,即loga(4/2)=1,所以a=2. (2)当0 由(1)(2)可得a=2或a=1/2. 例6已知2loga(x-4)>loga(x-2),求x的取值范围. 解析由题意可得x>4,原不等式可变为loga(x-4)2>loga(x-2). 当a>1时,函数y=logax为定义域内的增函数, ∴(x-4)2>x-2,x>4,可得x>6. 当0 ∴(x-4)2 综上所述,当a>1时,x的取值范围为(6,+∞); 当0 注:底数的范围不同决定了函数的单调性不同,所以一定要对底数进行讨论. 例7已知f(x)=(3a-1)x+4a(x<1),logax(x≥1)都是减函数且恒有f(x)>logax,那么a的取值范围是多少? 解析∵g(x)=logax(x≥1)是减函数, ∴0 ∵f(x)=(3a-1)x+4a(x<1)为减函数, ∴3a-1<0,∴a<1/3. 又∵f(x)=(3a-1)x+4a>logax恒成立, ∴(3a-1)×1+4a≥0.∴a≥1/7.∴a∈[1/7,1/3). 例8若f(x)=(3-a)x-4a(x≤1),log5ax(x>1)是增函数,且恒有f(x) 解析∵f(x)=(3-a)x-4a(x≤1),log5ax(x>1)是增函数, ∴得知3-a>0,5a>1,log5a1≥3-5a, ∴a∈[3/5,3). 注:函数单调性的一致性,要求端点值的大小关系也是确定的. 总之,同学们在解答对数函数题时,一定要从对数函数概念和定义入手,充分利用对数函数图象的特征点来分析,正确迅速地找到解题途径,从而得出正确答案,这对激发学习兴趣,提高数学素养也有重要意义.二、因忽略复合函数的定义域易致错
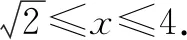


三、因忽略对底数的讨论易致错
四、因忽略分段函数的定义域分界点易致错

