函数极值点偏移问题的推广

张治国

(山东省济南市历城第二中学 250100)

本文从导函数的凹凸性的这一函数的重要性质出发，对一个与函数有关的不等关系进行了猜想与严格的证明，借助高等数学微积分理论中的拉格朗日中值定理，对函数极值点偏移的定义进了一般推广.

一、一个与函数有关的不等关系的猜想与证明

为了叙述方便，本文中所给出的函数f(x)在定义域上为连续且可导的函数.

设f(x)为定义在区间I上的函数，f′(x)为f(x)的导函数，取I上的任意两点x1,x2;

(1)若f′(x)为严格凸函数，则有如下不等关系：

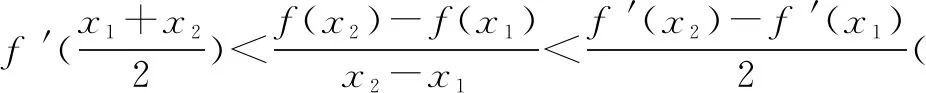
(2)若f(x)为严格凹函数，则有如下不等关系：

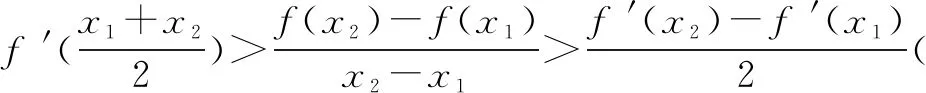
1.不等关系的几何解释

以公式一为例：

首先给出凸函数的一条重要的几何性质：若f(x)为凸函数，则其曲线总是在它的任意切线上方.

设f′(x)为函数图象在第一象限上的严格凸函数，大体图象如下：

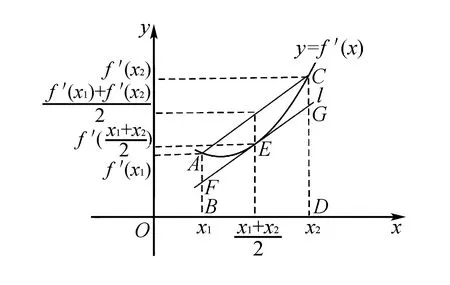
设梯形ABCD的面积为S1,梯形BDGF的面积为S2,曲边梯形ABCD的面积为S.根据定积分的几何意义,有S=f(x2)-f(x1).通过几何直观，有如下不等关系：

从上述的推导过程，可以得到公式一的几何解释.下面我们从理论上对公式一进行证明.

2.理论证明

下面从严格凸函数的定义出发，给出公式一的理论证明.

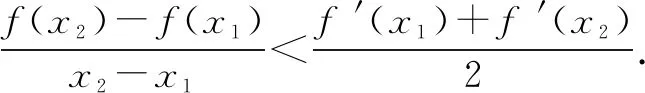
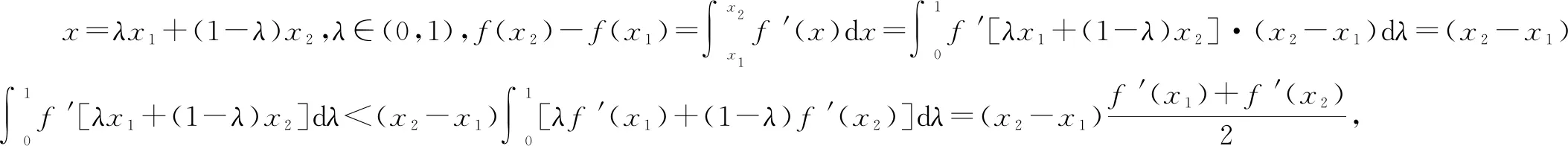
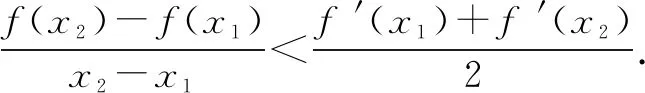
上述推导过程，借助高等数学微积分中有关凹凸函数的定义与性质进行了详细的证明.

二、函数极值点偏移问题的推广

结合拉格朗日中值定理由公式一与公式二，可以得到以下不等关系：

设f(x)为定义在区间I上的函数，f′(x)为f(x)的导函数，取I上的任意两点x1,x2;

若f′(x)为严格凸函数，则有如下不等关系：

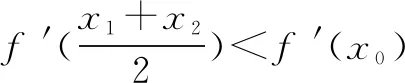
若f′(x)为严格凹函数，则有如下不等关系：

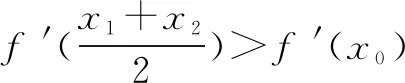
函数极值点偏移的定义是公式三与公式四的特殊形式.类比极值点偏移的定义，根据拉格朗日中值定理与公式三、公式四，我们可以将极值点偏移的定义大胆地进行一般推广，即一般偏移.下面给出一般偏移的定义.

导数既是高中数学函数部分的延续.对高考导数压轴题的研究，不仅仅要研究解法与技巧，更重要的是研究题目的背景与命题来源.借助高等数学中的微积分理论，能够为高考导数压轴题的研究提供新的视角.