新高考背景下数形结合思想的应用研究
——以函数性质探究为例
杨 兵
(贵州省黔东南州民族高级中学 556000)
在《普通高中数学课程标准》中明确指出了,在高中数学课堂教学中,教师要全面加强学生对图形的理解,提高学生空间思维想象能力,因此,教师要在课堂教学中引导学生进行主动思考,构建代数和图形之间的联系,进而调动学生学习的积极性、主动性.鉴于此,在新课程标准的要求下,教师必须要改变传统的课堂教学模式,借助数形结合思想内涵,将复杂的数学知识进行转化,使其成为直观的图象,进而引导学生在直观地观察中、理解思路、实现高效地学习.
一、数形结合思想概述
数形结合是一种重要的数学思想,还是一种有效的数学解题方式.就最近的几年高考来说,数形结合思想在高考中占据十分重要的地位.结合最近的高考试题研究分析,其中约有三分之一的题目可以利用数形结合的思想进行解答,尤其是在高考数学选择题、填空题目的处理中,通过数形结合思想的灵活运用,可对高考题目进行快速解答.
所谓的数形结合思想主要是指在具体的数学学习中,以数学问题作为出发点,并对数学题目中所隐藏的数量关系进行明确.之后,充分借助几何图形的形式,对题目中的数量关系进行表示,并结合一定的几何图形,将题目中的概念、性质等进行明确,并对其进行解决.在具体的高中数学课堂教学中,“数形结合思想”主要包括两种,即:(1)以形助数:主要是在具体的课堂教学中,借助几何图形,将代数问题进行阐明,进而使得复杂、抽象的代数问题更加直观、具体、生动.例如,在高中函数课堂教学中,函数式就属于复杂的、抽象的代数式,而函数图象则属于几何图形,借助函数图形对其性质进行讲解,可降低学生学习的难度;(2)以数辅形:主要是在课堂教学中,在着手对函数图象的性质进行探讨时,以代数作为手段,借助规范性、精确性的数字对图形中所呈现的某些性质进行描述.
二、数形结合思想在函数问题中的应用
1.在函数单调性判断中应用
在高中数学函数知识学习中,函数的单调性是其最为重要的性质之一,也是对函数进行研究的重要方向,是针对函数概念而进行的一种深层次的拓展和延伸.但是在传统的课堂教学中,受到多种因素的影响,学生对其理解存在较大的难度,以至于无法体会到学习的乐趣和成就感,久而久之就会使学生逐渐丧失学习兴趣.鉴于此,教师在有关函数单调性内容的教学中,就可以充分借助数形结合思想,将函数的单调性以图形的形式直观地呈现在学生面前,进而引导学生在图形的辅助下,对这一部分的内容进行有效的掌握.
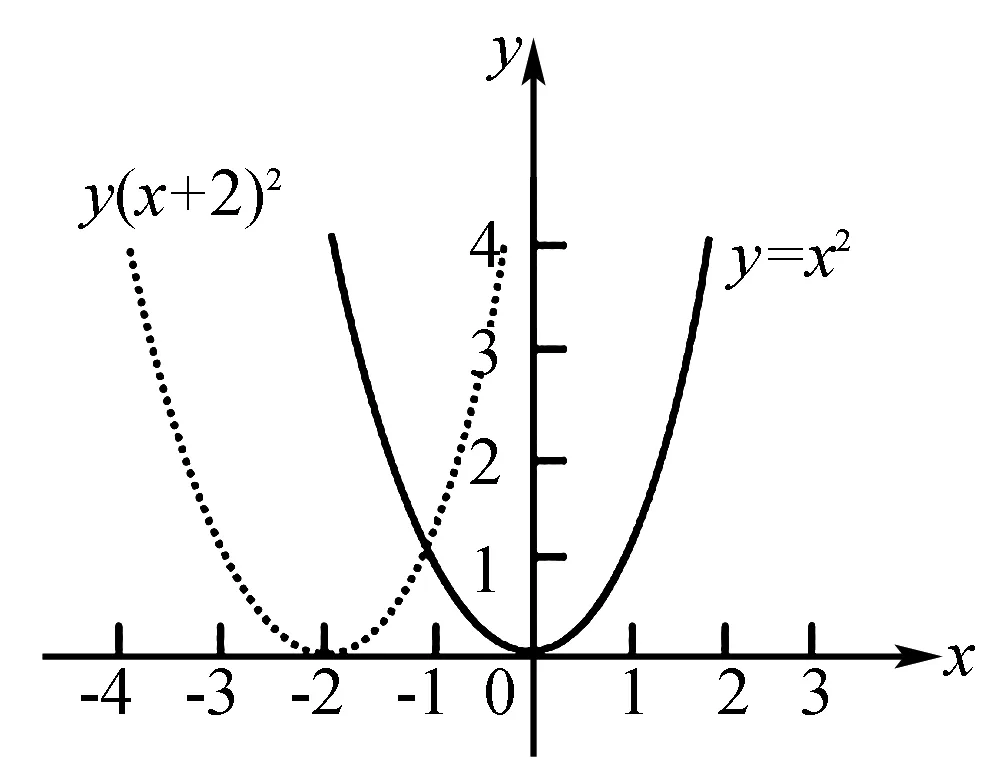
例如,在对二次函数“f(x)=x2+4x+4”明确单调区间,并对其单调区间的单调性进行确定的时候,为了进一步提升课堂教学效率,教师就可以引导学生对这一二次函数进行变形,使其成为f(x)=(x+2)2,如此一来,可使得函数图象更加直观.在具体对其解决的时候,教师就可以引导学生画出f(x)=x2的图象,之后通过平移的方式,将所画出的函数图象向左平移2个单位,即可得到f(x)=(x+2)2的图象(如右图).接着,教师可借助函数图象的形式,引导学生对其进行观察,在直观形象的图象中,对该函数的单调性做出准确的判断.接下来,教师还可以采用定义法的形式,引导学生对判断的结果进行验证,以确保所得出的结论更加严谨.
由此可以看出,在对函数单调性进行判断的过程中,通过数形结合思想的应用,使得抽象的问题更加具体化、形象化,进一步降低了学生学习中的难度,并在一定程度上提升了学生对函数的学习兴趣,促使其积极主动参与到课堂学习中.
2.在函数最值求法中应用
在高中数学函数课堂教学中,函数的最值求解是考试考查的重点.在对函数这一知识点进行学习时,由于其对学生的分析能力、逻辑思维能力、数学学习能力要求相对比较高,而学生在传统数学课堂教学模式下形成的固化了的解题思路,严重制约着学生的学习效果.鉴于此,教师在对这一部分内容进行教学时,也可充分借助数形结合思想,引导学生借助对图象的观察,对函数的最值进行明确和求解.

同时,学生在借助数形结合思想解决函数性质问题的时候,也打破了传统模式下的解题思路,促使学生在学习中,显著提升了其分析、逻辑思维能力等.长此以往下去,就会全面提升学生的数学学习能力.
综上所述,数形结合思想作为一种有效的数学学习方式,将其应用到高中数学函数性质教学中,简化了知识,降低了学习难度,极大地节省了学生在解题过程中所使用的时间,从而全面提升了学生的解题效率.

