一道高考题的7种解法

李昌成 李玉翠

(1.新疆乌鲁木齐市第八中学 830002；2.新疆乌鲁木齐市第64中学 830063)

近日在教学中遇到了一道老高考题，看起来很普通，细思极好，入口宽，解法多，是一个难得的高三复习素材.现分享于此，以飨读者.

一、题目呈现

(2014年浙江省高考文科数学卷第16题) 若实数a，b，c满足a+b+c=0，a2+b2+c2=1，则a的最大值为____.

二、总体分析

本题在代数背景下求最值，题设中有一次关系式，也有二次关系式，因此可以从方程、函数、一元二次不等式、均值不等式、解析几何、三角代换等多角度思考此题.虽然这是一道高考题，但也可以用初中知识解答它.由此可见，本题起点低，构思巧，教学价值高.

三、解法探究

视角1 从已知的二次方程入手.

构造以a为参数，关于b或c的二次方程，利用一元二次方程有解的充要条件作答.

解法1 由a+b+c=0得b=-(a+c)①,

将①代入a2+b2+c2=1得a2+[-(a+c)]2+c2=1，

整理得2c2+2ac+(2a2-1)=0.

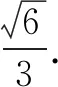
点评这种解法的关键在于消元，确定主元和参数.用一元二次方程有解的充要条件构造不等式.

视角2 从一元二次不等式入手.

通过消元，直接构造关于a的二次不等式，解不等式得a的最大值.

解法2 由a+b+c=0得b+c=-a，

由a2+b2+c2=1得b2+c2=1-a2.

因为b2+c2≥2bc，所以2(b2+c2)≥b2+2bc+c2，

即2(b2+c2)≥(b+c)2.

所以2(1-a2)≥(-a)2.

点评本解法结合题设的一次式、二次式的特征，通过运算，巧妙地彻底消元，同时构造了关于a的不等式.

视角3 从韦达定理入手.

将a看做参数，结合已知，通过推理运算用a表示b+c，bc，利用韦达定理构造一元二次方程作答.

解法3 由a+b+c=0得b+c=-a②,

将②平方得b2+c2=a2-2bc③,

将③代入a2+b2+c2=1得a2+a2-2bc=1，

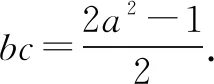
于是b，c是方程x2-(b+c)x+bc=0的实数解.

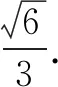
点评本解法在已知一次式的引导下，得到两根之和；在韦达定理的引导下，通过运算，寻找两根之积.构造方程是解题目标的需要，本质也在消元.

视角4 从函数观点入手.

从已知出发，构造一个关于b或c的二次函数，借助函数零点和最值作答.

解法4 由a+b+c=0得b=-(a+c)④,

将④代入a2+b2+c2=1得2c2+2ac+2a2-1=0.

构造函数f(x)=2x2+2ax+2a2-1⑤.

显然c是⑤的零点.

以下同解法1.

点评二次函数的最值与零点有密切的关系，题设中有二次关系，因此构造二次函数是情理之中的事.

视角5 从基本不等式入手.

本题中a，b，c的符号不确定，我们必须依托a2+b2≥2ab及其变形式作答.

解法5 将a+b+c=0平方得a2+b2+c2+2ab+2ac+2bc=0⑥.

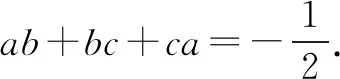
以下同解法1.

点评均值不等式是求最值的常见方法.关键在于怎样创造条件，使均值不等式出现，并包含所求量a.

视角6 从圆的参数方程入手.

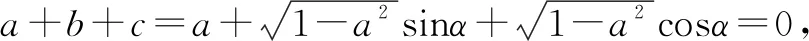
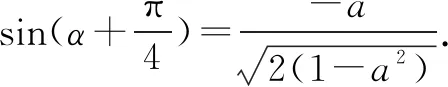
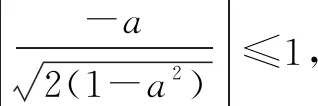
以下同解法1.

点评与圆联系起来的理由是已知的二次关系具备圆的方程特征，借助圆的参数方程有效的消元，借助三角函数的有界性得到关于a的不等式.

视角7 从直线和圆的位置关系入手.

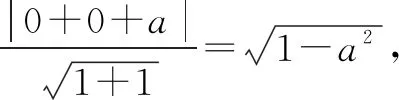
点评这种解法对学生的要求较高，跨越了代数与几何，利用数形结合将最值定格在边界位置处.只有深刻理解代数式的几何意义才能实现这个华丽转变.

四、解后反思

在高三复习过程中，一题多解能够帮助学生开拓思路，总结方法，优选解法，减少思维受挫.只要坚持深度研究题目，学生就可以从浩瀚的题海中解脱出来，避免刷题带来的繁重负担，取得事半功倍的效果.

这个题目的研究也显示了数形结合的重要性.前六种解法均存在一定的运算量，同时思维也存在一些急转弯，学生容易思维卡壳.第七种解法显得简洁明快，在“形”的指引下，解答直奔主题，胸有成竹.因此，我们学习中应高度重视数形结合思想的渗透和应用，让它变成一种自觉思维，经常主动思考代数问题背后的几何背景，让问题变得直观一些，解题时心理踏实一些，思路通畅一些，自然提升学习效率，培养核心素养.