2019年上海市春季高考数学试卷第12题的推广
2020-03-02 06:50甘志国
数理化解题研究 2020年4期
甘志国
(北京市丰台二中 100071)
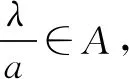
答案：-3或1.
本文将给出这道高考题的几个推广.
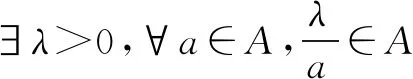
证明由0∉A，可得m (2)当0 综上所述，可得欲证结论成立. 证明由0∉A，可得m 由题设，可知 进而可得下面的三种情形： 由题设，可知 (3)当0 综上所述，可得欲证结论成立. 证明同结论2可证.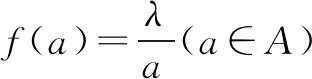
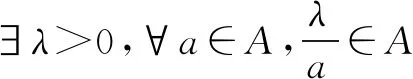
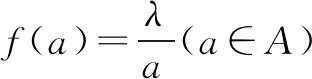
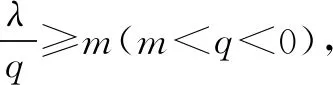
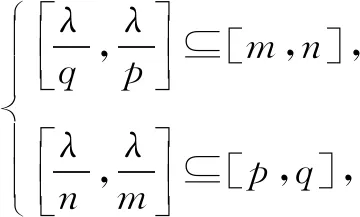
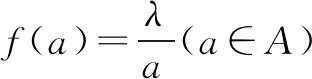
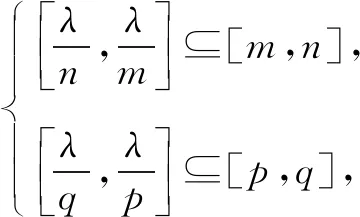
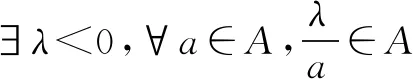猜你喜欢
快乐学习报·教育周刊(2022年15期)2022-05-05中国名牌(2021年10期)2021-10-21河北理科教学研究(2021年1期)2021-06-07数学大世界(2020年15期)2020-07-25中学生数理化(高中版.高二数学)(2019年3期)2019-04-27新高考·高二数学(2018年1期)2018-11-20消防界(电子版)(2018年15期)2018-02-18环球人文地理(2017年5期)2017-05-26商(2016年35期)2016-11-24中学数学杂志(2015年9期)2015-01-01
