鳖臑的形状
甘志国
(北京市丰台二中 100071)
题1 (2015年高考湖北卷理科第19题)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
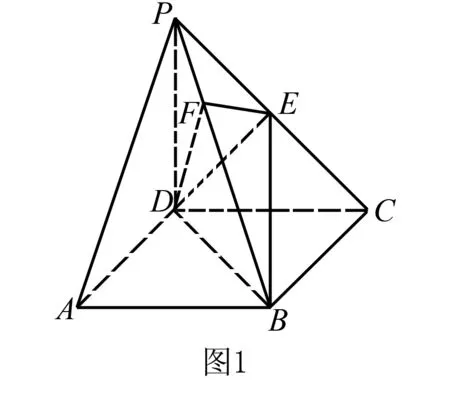
如图1,在阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE.
(1)证明:PB⊥平面DEF.试判断四面体DBEF是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由.
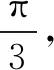
分析老师如何给学生讲解这道高考题呢?下面重点分析第(1)问的后半部分.
学生容易理解“将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马”,而难以理解“将四个面都为直角三角形的四面体称之为鳖臑”.
“鳖臑”长什么样,有“鳖臑”这样的几何体(四个面都为直角三角形的四面体)吗?
下面我们来想办法构造出鳖臑即四个面都为直角三角形的四面体.这自然会想到如图2所示的“墙角四面体OABC”:其中三条射线OA,OB,OC两两互相垂直(因而△OAB,△OBC,△OCA均是直角三角形).若△ABC也是直角三角形,则四面体OABC就是鳖臑.但我们可以证明△ABC是锐角三角形:
设OA=a,OB=b,OC=c,由勾股定理可得
AB2+AC2-BC2=(a2+b2)+(a2+c2)-(b2+c2)=2a2>0
在△ABC中,再由余弦定理可得
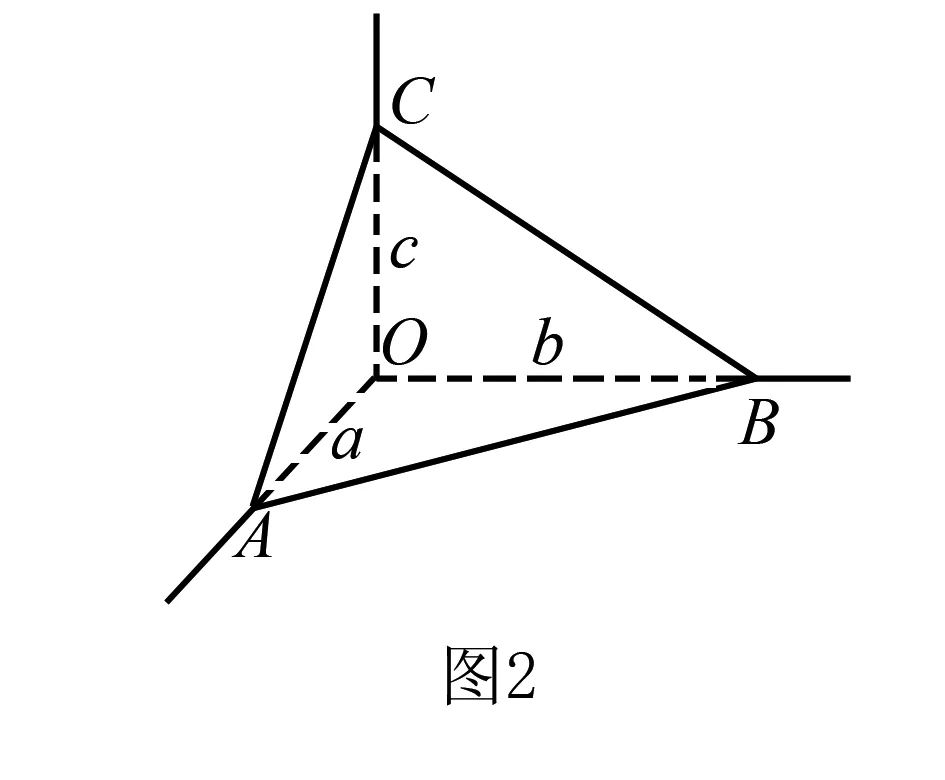
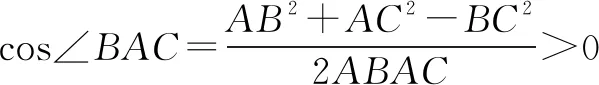
因而∠BAC是锐角.同理,可得∠ABC,∠ACB均是锐角,所以△ABC是锐角三角形.
说明由这种方法不能构造出鳖臑.必须另想它法.
借助长方体(长方体是一种常用的立体几何模型:它处处是“垂直”——有相交直线垂直,还有异面直线垂直;有直线与平面垂直,还有平面与平面垂直.它处处是“平行”——有直线与直线平行,还有直线与平面平行、平面与平面平行.还有异面直线、正四面体、“墙角四面体”等等图形.它们在解题时均很有用)来构造鳖臑是一种好方法:因为长方体中有很多直角,鳖臑的各个面都是直角三角形.可能有的同学已经得到了答案——放置在如图3所示的长方体中的四面体ABCD就是鳖臑:
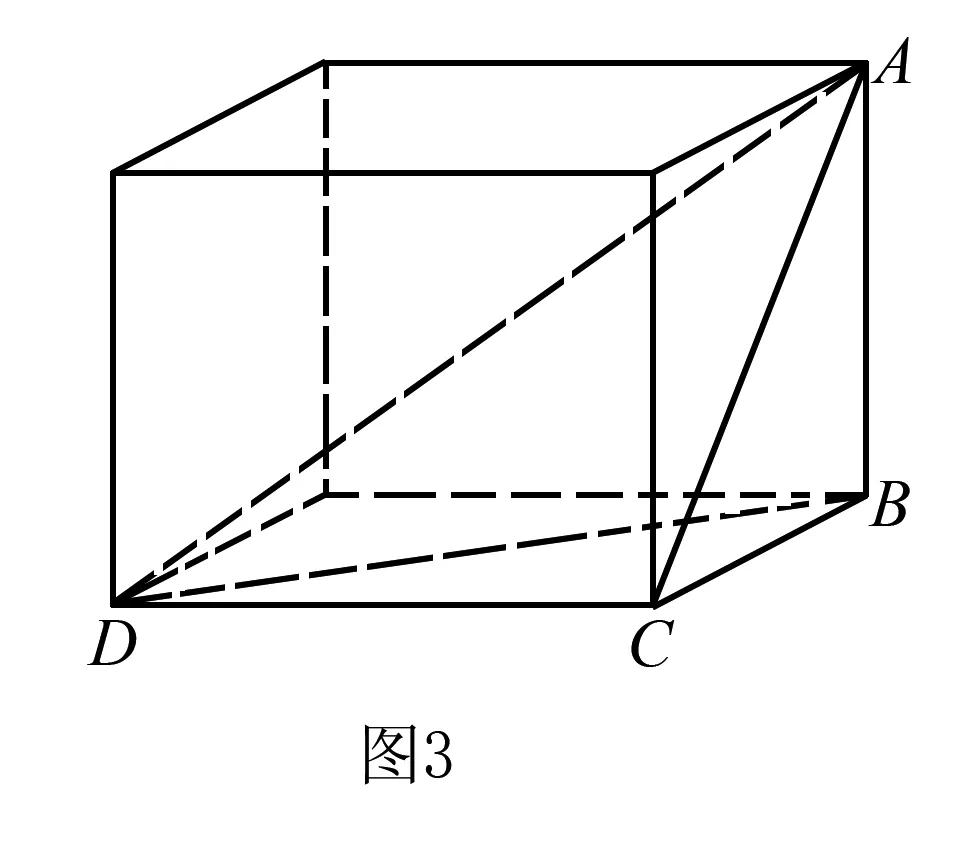
在鳖臑ABCD即三棱锥A-BCD中,∠BCD=90°,棱AB⊥底面BCD(且垂足是底面△BCD的锐角顶点,一定不会是直角顶点C,这是在图2中已经获证的).
还有其他现状的鳖臑吗?答案是否定的.
在如图4所示的鳖臑ABCD中,可设六条棱长分别是AD=a,AC=b,AB=c,DB=d,DC=e,BC=f.
(1)先证:在鳖臑的各个顶点处的三个角,至少存在一个顶点处有两个角是直角.
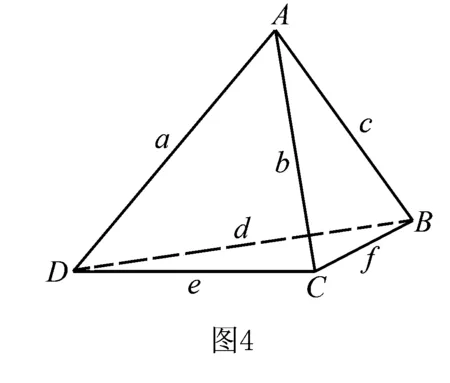
否则,在如图4所示的鳖臑ABCD的每个顶点处的三个角中,均有且仅有一个是直角(在下面的解答中,将反复运用这一假设).
在△BCD中可不妨设∠BCD=90°(可得d>e,d>f),因而∠ACD≠90°,∠ACB≠90°.
在△ABC中,因为∠ACB≠90°,所以∠CAB=90°或∠ABC=90°.
若∠CAB=90°,可得f>b,f>c,因而d>f>c,d>c,所以在△ABD中,AB=c不是最大边,∠ADB不是最大角,因而∠ADB<90°,可得∠ABD=90°.
可得鳖臑ABCD在点D处的三个角中只可能是∠ADC=90°,进而可得a>d>f>b>a,这不可能!所以∠ABC=90°.
因而在△ABD中,∠ABD≠90°,所以∠BAD=90°或∠ADB=90°.
若∠BAD=90°,可得鳖臑ABCD在点D处的三个角中只可能是∠ADC=90°,这样就得到空间四边形ABCD的四个内角均是直角,这将与“第八届(1976年)加拿大数学奥林匹克竞赛试题)在四边形ABCD中,∠ABC,∠BCD,∠CDA,∠DAB都是直角,求证:四边形ABCD是矩形”的结论(实际上,可以证明“空间四边形的内角和小于周角”)相矛盾!所以∠ADB=90°.
可得鳖臑ABCD在点A处的三个角中只可能是∠DAC=90°,进而可得c>d>e>b>c,这不可能!
证毕!
(2)再证:
定理鳖臑就是从一个Rt△BCD(可不妨设∠BCD=90°)的锐角顶点(可不妨设为点B)处作平面BCD的垂线段BA而后得到的四面体ABCD,鳖臑也是恰好是在两个顶点处的三个角中均恰有两个角是直角的四面体.
证明由(1)的结论可知,在如图4所示的鳖臑ABCD中,至少存在一个顶点处的三个角中有两个角是直角.
可不妨设在点C处的三个角中有两个角是直角,由“墙角四面体”不是鳖臑知,可不妨设∠ACB=∠BCD=90°,∠ACD≠90°,则在△ACD中,∠CAD=90°或∠ADC=90°.
① 若∠CAD=90°,可得∠ABD=90°或∠ADB=90°或∠BAD=90°.
若∠ABD=90°,可得a>d>e>a,这不可能!
若∠ADB=90°,由BC⊥AC,BC⊥CD,可得BC⊥平面ACD,所以AD⊥BC.再由AD⊥DB,可得AD⊥平面BCD,AD⊥CD,这将与AD⊥AC矛盾!
若∠BAD=90°,此时得到的鳖臑ABCD与图3中的鳖臑实质是一样的:从Rt△DAC(∠DAC=90°)的锐角顶点C作直线CB⊥平面ACD得到的四面体ABCD.
② 若∠ADC=90°,可得∠ABD=90°或∠BAD=90°或∠ADB=90°.
若∠ABD=90°,可得b>a>c>b,这不可能!
若∠BAD=90°,可得BC⊥平面ACD,所以AD⊥BC.再由AD⊥AB,可得AD⊥平面ABC,AD⊥AC.
又因为AD⊥CD,所以A,C,D三点共线,这不可能!
若∠ADB=90°,此时得到的鳖臑ABCD与图3中的鳖臑实质是一样的:从Rt△DAC(∠ADC=90°)的锐角顶点C作直线CB⊥平面ACD得到的四面体ABCD.
下面再来解答题1的第(1)问:
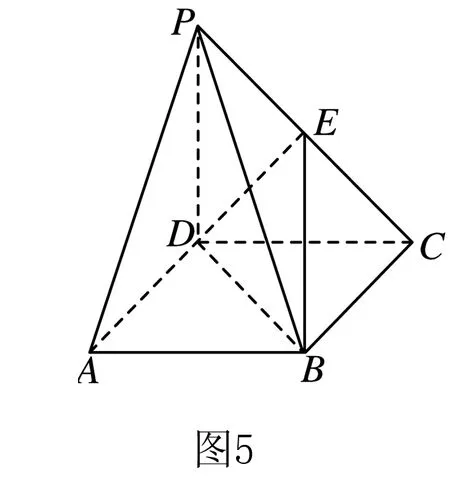
可先作出如图5所示的鳖臑WXYZ,其中∠XYZ=90°,WZ⊥平面XYZ.
我们由图5这个模型来求解第(1)问的后半部分:
可得∠DEF=90°(由AD⊥平面PDC,AD∥BC,可得BC⊥平面PDC,DE⊥BC;又由DE⊥PC,可得DE⊥平面PBC,所以DE⊥EF),再由第(1)问的前半部分证得的结论“PB⊥平面DEF”,可得:若题1中的四面体DBEF是鳖臑,则其顶点D,B,E,F分别对应着图5中鳖臑WXYZ的顶点X,W,Y,Z.
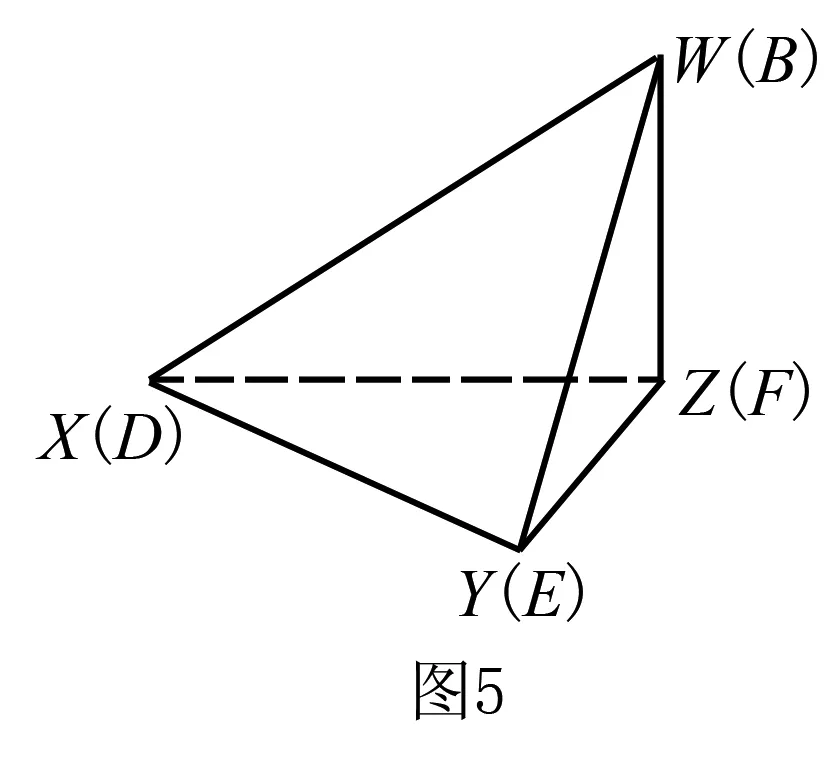
易知图5中鳖臑WXYZ中各个面的直角分别是∠XYW,∠XYZ,∠YZW,∠XZW,因而题1中的四面体DBEF各个面的直角分别是∠DEB,∠DEF,∠EFB,∠DFB.
再来解答题1的姊妹题就很容易了:
题2 (2015年高考湖北卷文科第20题)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
在如图6所示的阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD,点E是PC的中点,连接DE,BD,BE.
(1)证明:DE⊥平面PBC.试判断四面体EBCD是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由.