例谈以函数切线为背景的不等式问题
陈俊艺
(福建省晋江市毓英中学 362251)
高考数学试卷中,导数作为重要的考点之一,常作为压轴题来考查.导数的解答题综合性强,区分度高,可以很好地考查学生的能力.而不等式的证明和已知不等式成立求参数范围是常见的题型.深入挖掘这些题目的背景,可以发现很多和函数切线有关.利用切线来逼近曲线,很好地体现了微积分中最基本的思想——“以直代曲”.本文通过几个例题来谈谈这个问题.
一、试题呈现
例1(2017年全国Ⅱ卷文科21题)设函数f(x)=(1-x2)ex,
(1)讨论f(x)的单调性;
(2)当x≥0时,f(x)≤ax+1,求a的取值范围.
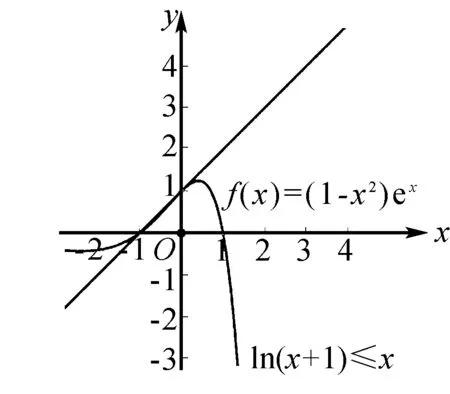
图1
分析(2)利用几何画板画出函数f(x)的图象如图所示,当x∈[0,+)时,f(x)为凸函数.直线y=ax+1经过(0,1),所以当射线y=ax+1(x∈[0,+))位于切线y=x+1位置或上方时f(x)≤ax+1成立.反之则f(x)≤ax+1不恒成立.
解答(1)略.(2)f(x)=(1+x)(1-x)ex.
当a≥1时,设函数h(x)=(1-x)ex,h′(x)=-xex<0(x>0),因此h(x)在[0,+∞)单调递减,而h(0)=1,故h(x)≤1,所以f(x)=(1+x)h(x)≤x+1≤ax+1.
当0
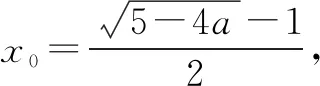
则x0∈(0,1),(1-x0)(1+x0)2-ax0-1=0,故f(x0)>ax0+1.与题设矛盾.
综上,a的取值范围是[1,+∞).
本题以切线为背景,本质应该是函数的凹凸性问题,f(x)≥ax+b(f(x)为凹函数)或者f(x)≤ax+b(f(x)为凸函数)恒成立的问题常常可以转化为直线y=ax+b位于函数f(x)的切线位置或切线的下(上)方的问题来加以解决.
二、“切线不等式”的应用
根据y=ex,y=lnx的图象以及它们的切线,容易得到下面的不等式:ex≥x+1,当且仅当x=0时等号成立;lnx≤x-1,当且仅当x=1时等号成立.
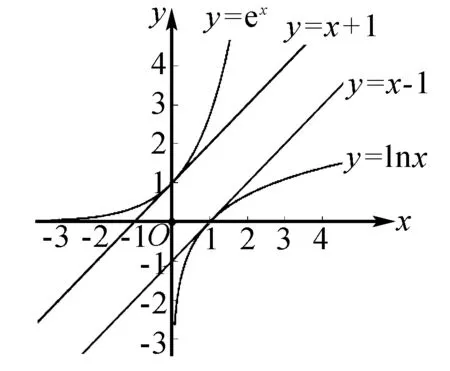
图2
这里把它们称为“切线不等式”.

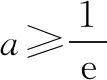
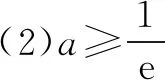
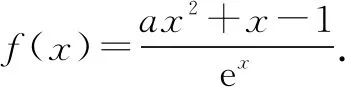
(1)求曲线y=f(x)在点(0,-1)处的切线方程;
(2)证明:当a≥1时,f(x)+e≥0.
解(1)易求得切线方程是2x-y-1=0.
(2)f(x)+e≥0⟺ax2+x-1+ex+1≥0.
当a≥1时,ax2+x-1+ex+1≥x2+x-1+ex+1.
x2+x-1+ex+1≥0⟺x2+x-1+x+2≥0⟺(x-1)2≥0.
通过上面两个高考试题可以发现“切线不等式”对我们解题中有很大的帮助.在高考中以“切线不等式”为背景的试题还有很多,这里就不一一列举.
三、利用切线进行放缩
上面的两个例子用“切线不等式”进行放缩来证明不等式或者求参数的范围.下面我们一起来看几个与函数零点有关的不等式的证明问题.
例4(2018年石家庄一模理科21题)已知函数f(x)=(x+b)(ex-a)(b>0)在(-1,f(-1))处的切线方程为(e-1)x+ey+e-1=0.
(1)求a,b;
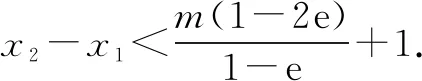

图3

本题涉及函数的双零点,这是近几年的热点问题.利用切线作为媒介来对两个零点进行放缩,巧妙地解决这个题目,很好的体现了数形结合的思想,培养了学生的直观想象素养.
四、求双参数最值
在导数的压轴题中经常会涉及到参数,其中常见的一种思路是把“双参”变为“单参”,这里和大家分享几道以切线为背景的求双参最值的问题
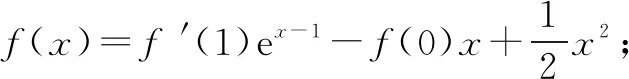
(1)求f(x)的解析式及单调区间;

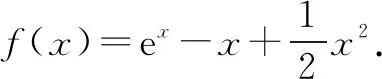
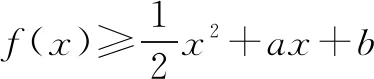
即曲线y=ex恒在直线y=(a+1)x+b上方或者与之相切.
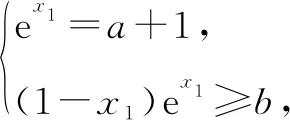
故(a+1)b≤e2x1(1-x1).
记g(x)=e2x(1-x),g′(x)=e2x(1-2x),
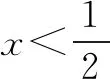
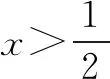
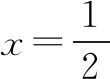
这些与函数的切线有关的试题,很好地考查了学生的函数与方程,数形结合,转化和化归思想.通过上面的题目的解答,可以发现对于导数综合题,老师应该指导学生重视函数的图象,利用数形结合来指引我们的解题思路,从而在问题的解答上有所突破.

