三招破解以三角形为背景的多元变量最值问题

孙 磊

(江苏省无锡市第三高级中学 214000)

众所周知，求解多元变量最值问题的关键在于减少变元，我们可以从三角、形、数三个角度寻找突破口.

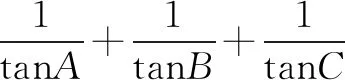
分析这道题含有A，B，C三个变量，解决本题的关键在于如何将已知条件2sin2A+sin2B=2sin2C转化成tanC=3tanA，并且将tanB也用tanA来表示.

方法1 边角互化

∵2sin2A+sin2B=2sin2C,

∴2a2+b2=2c2.

在△ABC中，a2=b2+c2-2bccosA，代入上式，

∴3b=4ccosA，

即3sinB=4sinCcosA。

在△ABC中，sinB=sin(A+C)=sinAcosC+cosAsinC,代入上式，

∴3sinAcosC=sinCcosA，

∴tanC=3tanA.

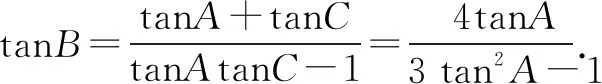
原式

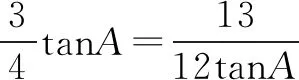
点评以三角函数的化简作为突破口，通过边角互化实现减少变元，过程流畅自然，但是需要有较强的三角运算功底，如果三角公式不能熟练应用，这种方法对学生来说有时候会有一定难度.

方法2斜化直

过点B作BD⊥AC，交AC于D.

设BD=h，AD=x，CD=y

在Rt△BDC中a2=h2+y2，在Rt△BDA中c2=h2+x2，b=x+y.

∵2sin2A+sin2B=2sin2C,

∴2a2+b2=2c2.

∴2(h2+y2)2+(x+y)2=2(h2+x2)2,

∴x2-2xy-3y2=0，即(x+y)(x-3y)=0,

∴x=3y.

∴3tanA=tanC.

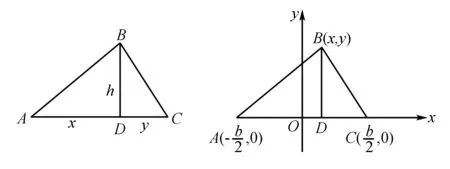
以下解法同法1

点评用构造直角三角形来表示三角函数是一种非常直观的化简方式，这种方法的解题关键是要在代数运算的过程中消去中间变量h，然后找到三角形的边或者角的内在关系.

方法3建系设点

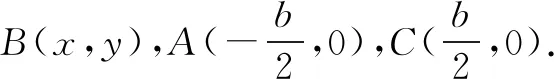
∵2sin2A+sin2B=2sin2C,

∴2a2+b2=2c2,

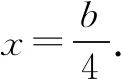
∴AD=3CD,即3tanA=tanC.

以下解法同法一.

点评通过建系设点，数形结合思想确定动点轨迹，将三角问题转化成函数求最值问题是解决这类题目的一个新视角，其难点在于如何建系，寻找哪个点的轨迹作为突破口.

例2在△ABC中，A,B,C所对的边分别是a,b,c，已知sinA+sinB+μsinAsinB=0，且a+b=2c，则实数μ的取值范围是____.

方法一边角互化

∵a+b=2c，

∴sinA+sinB=2sinC.

方法二斜化直

直过C作CD⊥AB，交AB于D，设CD=h，BD=x,AD=c-x.

又∵a+b=2c,

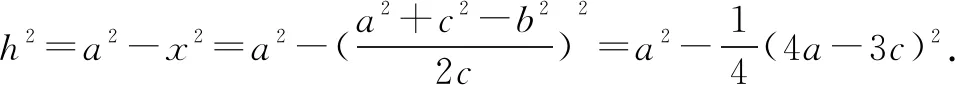
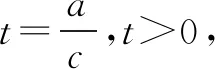
∵μ<0,

方法3建系设点

以AB中点为原点，AB为x轴，AB的中垂线为y轴如图建系.

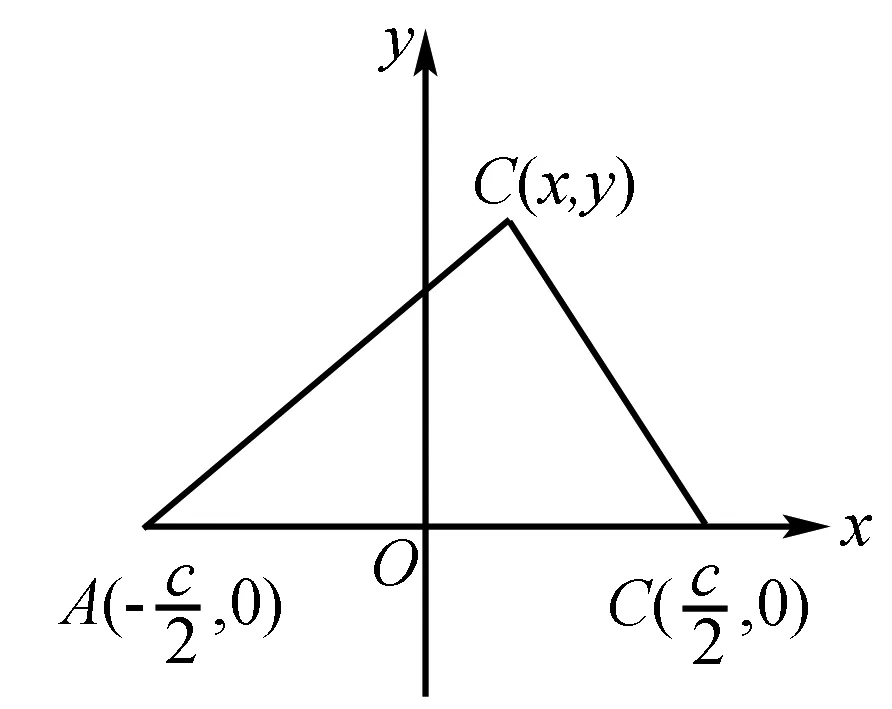
设C(x,y),∵a+b=2c，即CA+CB=2c,

∴C的轨迹是以A,B为焦点，2c为长轴的椭圆.

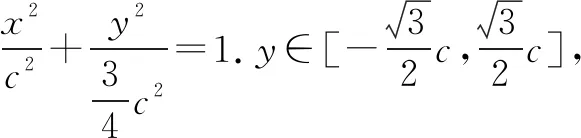
∵sinA+sinB+μsinAsinB=0.

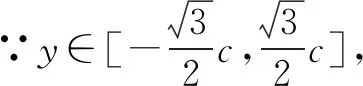
上面两个例题用三种方法都能解决，但不是所有类似问题都能同时用这三种方法解出.斜化直的方法利用构造直角三角形表示出三角函数，这个过程会产生一个中间变量h，只有当已知等式是齐次式才有可能消去中间变量，否则这种方法就行不通.建系设点的方法归根结底是用代数方法求最值，因此已知条件必须含有长度关系或者已知的三角关系能够转化成长度关系，否则这种方法就行不通.边角互化的方法应该是适用范围最广泛的一种方法，在使用这种方法解题的时候需要明确化简方向，熟悉三角公式.总之，同学们在做这类题目的时候，应该先观察题目的特点，结合自身知识储备选择合适的方法.