高中数学数列求和的常用方法

◎龚 言 李 敏 （.北华大学数学与统计学院，吉林 吉林 303；.吉林省磐石市第五中学校，吉林 磐石 3300）

数列求和的常用方法有：公式法、分组求和法、倒序相加法、裂项相消法、错位相减法、并项求和法.

一、公式法

此方法具有很强的针对性，观察数列通项公式，如果一个数列是等差数列或是等比数列，即可直接用等差或等比数列的前n项和公式求解.

例1已知数列｛an｝是等比数列，公比q＜1，且a2＝2，a1＋a2＋a3＝7.

（1）求｛an｝的通项公式；

（2）设bn＝log2an，求数列｛bn｝的前n项和.

解（1）由已知，得

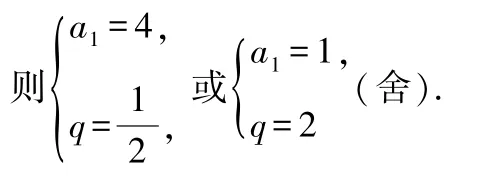
所以an＝ 23－n.

（2）因为bn＝log2an＝log223－n＝ 3－n，所以数列｛bn｝是以2 为首项、－1 为公差的等差数列.

设数列｛bn｝的前n项和为Tn，

二、分组求和法

分组求和法一般适用于通项公式为如下两种形式的数列：

（1）若an＝bn±cn，且｛bn｝，｛cn｝为等差数列或等比数列，可采用分组求和法求｛an｝的前n项和.

｛bn｝，｛cn｝是等比数列或等差数列，可采用分组求和法求和.

例 2已知数列｛an｝的通项公式an＝ 2n＋n.求a1＋a2＋a3＋…＋an的值.

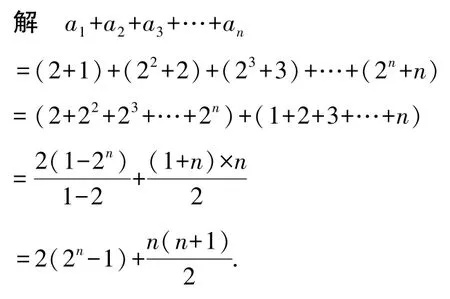
反思与感悟一些数列通过适当分组，可以得到两个或几个等差数列或等比数列，进而利用等差数列或等比数列的求和公式分别求和，从而得出原数列的和.

三、倒序相加法

如果一个数列｛an｝，与首末项等距的两项之和等于首末两项之和，那么求这个数列的前n项和可用倒序相加法，如等差数列的前n项和即用此法推导的.

例 3已知f（99）＋f（100）的值.

解由题意，得

四、裂项相消法

如果一个数列的通项可拆成两项之差，然后重新组合，使中间的项可以相互抵消，那么求此类数列前n项和用裂项相消法，裂项相消求和经常用到的拆项公式如下：

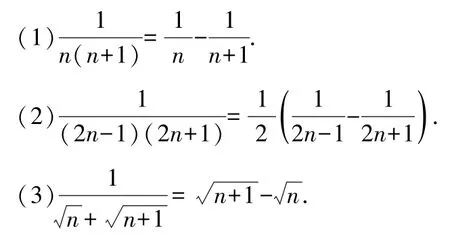
例4求的和.

解∵此数列的前n项和

反思与感悟若数列的通项公式可以化为f（n＋1）－f（n）的形式，则在数列求和时，就可以采用裂项相消法.要注意相消后的项要对称，若前面留下两项，则后面也要留下两项.

五、错位相减法

若一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的，则这个数列的前n项和即可用此法来求，如等比数列的前n项和公式就是用此法推导的.

例 5已知数列｛an｝的通项公式an＝2n－1（n∈N∗），

数列｛bn｝满足

求｛bn｝的前n项和Tn.

解设

则当n≥2 时，

所以有

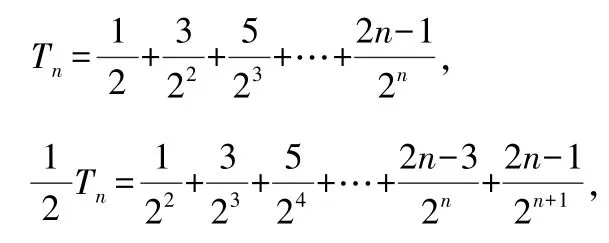
两式相减，得

所以

反思与感悟用错位相减法求和时应注意：（1）要善于识别题目类型，特别是等比数列公比为负数的情形；（2）在写出“Sn”与“qSn”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“Sn－qSn”的表达式.若公比是个参数（字母），则应先对参数加以讨论，一般情况下分等于1 和不等于1 两种情况分别求和.

六、并项求和法

若一个数列的前n项和可两两结合求解，则称之为并项求和.形如an＝（－1）nf（n）的类型，可采用两项合并求解.

例 6求Sn＝－1＋3－5＋…＋（－1）n（2n－1）.

解当n为奇数时，

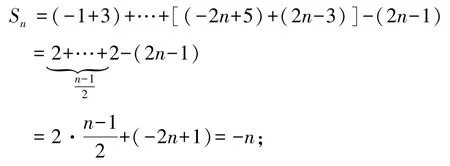
当n为偶数时，

综上，

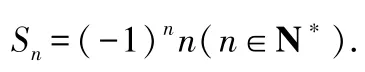
反思与感悟当数列中的项正、负相间时，通常采用并项求和法，但应注意对n的取值的奇偶性进行讨论.其结果有时可以统一书写，有时要分段书写.

总而言之，在求数列的前n项和的具体问题中，首先要认真观察这个通项公式的特征，然后选择恰当的方法，在平时的学习和训练中，学生要注意举一反三，从一道题目解答过程中寻求同一类题目的共性特征，从而提高自己的解题能力.