化归法在解数学题中的应用

◎艾 玲 （沈阳理工大学理学院，辽宁 沈阳 110159）

化归，就是把新问题转化为已经解决的问题，许多数学问题在解法上凝聚与蕴含着化归思想.那么，在实际应用中如何进行化归，又向何处化归呢？ 主要有三条途径：向基本数学模型化归，一般向特殊化归，高层次向低层次化归.

一、向基本数学模型化归

我们知道，模型法是数学反映现实世界的基本方法.对于数学模型，已经建立了模式化的解题方法，若能把问题化归到已知的数学模型中，则解决问题的方法就由这种模型的模式化的方法呈现出来.这里以函数模型和复数模型为例作一说明.

（一）化归到函数模型

用导数判断函数的性态给我们提供了很有应用价值的模型，在此介绍函数的导数模型.

例1已知a，b为实数，且 e＜a＜b，其中 e 为自然对数的底，求证：ab＞ba.

思考欲证ab＞ba，只需要证blna＞alnb，即证需要证在（e，＋∞）内是减函数即可.

证明设

所以当 e＜a＜b时

即blna＞alnb，

亦即ab＞ba，证毕.

（二）化归到复数模型

例 2求二元函数的最小值.

所以f（x，y）≥8，

等号当且仅当 argz1＝argz2，

即x＝1，y＝3 时，f（x，y）取得最小值，最小值为 8.

本例是通过构造复数 z1，z2，并用其表示f（x，y），将所求问题化归到复数模型上去.

二、向特殊化归

对于一般性问题，我们总希望通过一些手段化为特殊的，再借助特殊性将一般性问题解决. 向特殊化归的方法有许多种，这里以常见的正交变换为例说明化归法的基本思想.

正交变换具有保持向量长度及夹角等度量不变的性质，即具有保持几何形状不变的优点. 还有一些方法（对应有多个可逆的线性变换）能把二次型化成标准型，如配方法、雅可比法等，注意到在一般的可逆线性变换之下，向量的长度要改变. 因此，正交变换是直角变换，它符合解析几何的要求.

例3作直角坐标变换，把二次曲面方程

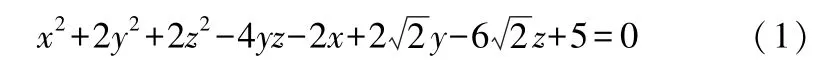
化成标准方程，并指出它是什么曲面.

解首先把二次曲面的二次项部分用正交变换化成平方和的形式. 设

该二次型的矩阵是

求出A的特征值λ1＝ 1，λ2＝ 4，λ3＝ 0，不难求得正交矩阵

作正交变换

把二次型f化成标准形为f＝x′2＋4y′2.

因此作直角坐标变换（2），也就是把

代入二次曲面方程（1），整理，得

将新方程的左端配方，得

作坐标系的平移

得到在直角坐标系O∗－x∗y∗z∗下的方程

上式是二次曲面（1）的标准方程，它是椭圆抛物面. 把式（3）代入式（2）就得到化方程（1）为标准方程的直角坐标变换公式如下：

可见要判断二次曲面的类型，需要用直角坐标变换将其中三元二次型部分的交叉项消去，即变成标准形，再通过坐标平移，即可得到二次曲面的标准方程. 变换就是改变形式，对于不同的数学对象，变换的形式和手法也是不同的，这里就不一一举例了.

三、高层次向低层次化归

一般地，事物的发展遵循从低层次向高层次过渡，但解决问题时，常把高层次逐步化归到低层次，把复杂化归到简单.这里以解高阶微分方程为例说明化归的基本思想.

高阶方程没有一般解法，但对于几类特殊的高阶方程，可采用适当的变量置换化归为低阶方程来求解.

（1）y（n）＝f（x）逐次积分即可求解

（2）y″＝f（x，y′）方程不明显含y

令y′＝p，则

方程可化为关于x，p的一阶方程

（3）y″＝f（y，y′）方程不明显含x

令y′＝p，则

方程可化为关于y，p的一阶方程

例 4求解

分析方程不明显含y，同时又不明显含x，故有两种解法，这里只给出其中一种解法.

解令y′＝p，则方程可化为

解得y′＝p，

积分，得方程的通解（x＋C1）2＋（y＋C2）2＝1.

综上所述，可以看出化归法的应用范围很广，但化归法的应用比较灵活，没有固定的程式，对不同的问题要具体分析.学生只要平素多做练习，注意积累解题经验和技巧，化归法并不难掌握.