关于矩阵乘积秩的一种简捷证明
2020-09-11 13:41孔妮娜北方民族大学数学与信息科学学院宁夏银川750021
数学学习与研究 2020年11期
◎孔妮娜 (北方民族大学数学与信息科学学院,宁夏 银川 750021)
一、基本概念及定理
已知矩阵

如果把矩阵A的每一行看成一个向量,则

称为矩阵A的行向量组.
如果把矩阵A的每一列看成一个向量,则

称为矩阵A的列向量组.
定义[1]矩阵A的行向量组的秩称为矩阵A的行秩,矩阵A的列向量组的秩称为矩阵A的列秩,且矩阵A的行秩与列秩相等,统称为矩阵A的秩.
参考文献[1]中给出的关于矩阵乘积秩的定理如下:
定理[1]设A是数域P上s×n矩阵,B是数域P上n×m矩阵,于是

即矩阵乘积的秩不超过各因子的秩.
二、主要结果
本文用一种简捷的方法证明了矩阵乘积秩定理,并举例说明定理的结论成立.
定理的证明要证明式(1)成立,只需要证明秩(AB)≤秩(A),同时秩(AB)≤秩(B).下面分别证明这两个不等式.
(1)首先证明秩(AB)≤秩(B).
已知

设β1,β2,…,βn表示矩阵B的行向量组,则

则矩阵C的第i行元素分别为

令γ1,γ2,…,γs表示矩阵C的行向量组,则
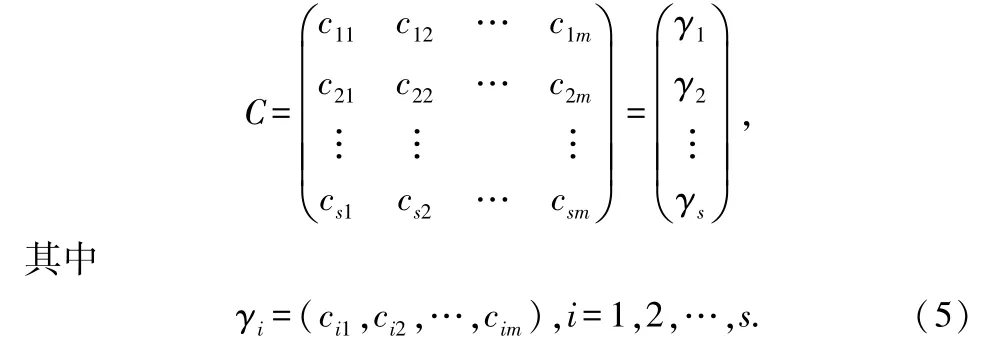
把式(4)带入式(5),得

即矩阵C的行向量组γ1,γ2,…,γs可以由矩阵B的行向量组β1,β2,…,βn线性表出,所以


(2)其次证明秩(AB)≤秩(A).
令α1,α2,…,αn表示矩阵A的列向量组,则

由式(2)和式(3)可知,矩阵C的第j列元素分别为

如果令μ1,μ2,…,μm表示矩阵C的列向量组,则

把式(6)带入式(7),得

即矩阵C的列向量组μ1,μ2,…,μm可以由矩阵A的列向量组α1,α2,…,αn线性表出,所以


综上所述,结论成立.
例已知矩阵
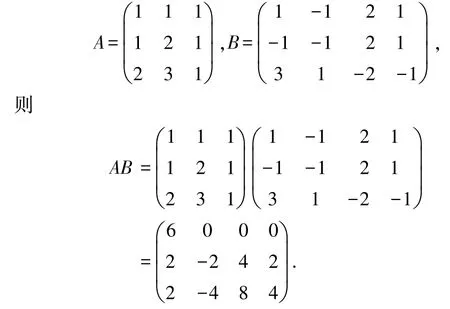
下面利用矩阵的初等行变换分别计算矩阵A、B及AB的秩:

猜你喜欢
中学生数理化·七年级数学人教版(2023年3期)2023-03-21
中等数学(2022年7期)2022-10-24
小学生学习指导(中年级)(2021年3期)2021-04-06
学生导报·东方少年(2019年23期)2019-12-30
数学年刊A辑(中文版)(2018年1期)2019-01-08
科教导刊·电子版(2017年31期)2018-01-09
西部论丛(2017年11期)2017-01-15
数学年刊A辑(中文版)(2014年2期)2014-10-30
小学生导刊(高年级) (2006年6期)2006-06-27

