求收敛的数项级数“和”的若干典型方法

◎黄毅蓉 （成都航空职业技术学院，四川 成都 610100）

1 引言

2 方法论述

2.1 利用数项级数自身求数项级数的“和”

2.1.1 直接求解法（定义法）

例1求级数的和.

解由上，此时

说明：只要等比级数满足公式（1） 的条件，均可以用公式（1） 求和.

2.1.2 方程式法

方程式法是利用一些运算技巧对部分和数列构造方程表达式，进而得到部分和数列的和式表达，再取极限求得数项级数的“和”.

例2求数项级数的和.

解可以判定此级数是收敛且绝对收敛.设sn＝1－

上面两式相加有：

2.1.3 通项拆项法

通项拆项法是将数项级数的通项进行拆分，将部分和数列简化后再取极限求数项级数的“和”.

定理1数项级数若un＝an － an＋1，且a，则

例3求级数的和.

定理1 的一种变形为：

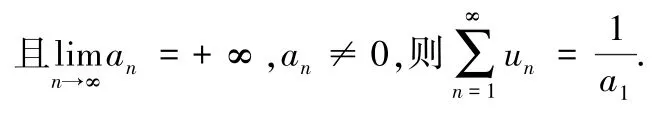
例4求级数的和.

解此时数项级数的通项

由an＝n，且

2.1.4 间接求和法

间接求和法是通过级数运算、级数性质将某些未知的数项级数表示为已知的收敛级数的线性组合，从而求得“和” 值.

2.2 利用幂级数求数项级数“和”

2.2.1 幂级数定值法

利用幂级数定值法的关键在于针对收敛的数项级数构造一个对应的幂级数.

例6求数项级数的和.

解构造形如的幂级数，当x＝ 3 时即为上述数项级数.

逐项求导，得

2.2.2 幂级数阿贝尔定理法

阿贝尔的幂级数连续定理：

在应用阿贝尔定理求数项级数和时，首先要依据所给数项级数适当地设置一个幂级数，再求出此幂级数的和函数.定理表明和函数在x＝1 处是左连续的，最后对和函数求极限，从而求出收敛数项级数的和.

例7求数项级数的和.

解构造幂级数其收敛区间是（－1，1］.

2.3 利用傅里叶级数求数项级数“和”

nancosnωx0＋bnsinnωx0，而x0是傅里叶级数展开式收敛区间的点，所以有此法也称傅里叶级数的定值法.

例8求数项级数的和.

解将［－π，π］上的函数f（x）＝x2做周期为2π 的周期延拓，并做傅里叶级数展开.

因为f（x）＝x2为偶函数，

2.4 利用复级数求数项级数“和”

利用复级数求数项级数和的方法一般称为三角级数法，主要是求级数的和，通常把它们视为复数域内的复级数此时z＝eix， 然后对求和，并将其展成实部与虚部，则所求级数就是此复级数的实部与虚部对应的系数，从而求出“和”.

例9求的和.

解因为 cosnπ＝ （－1）n，n＝ 0，1，2，…所以

令z＝eix，考虑复级数

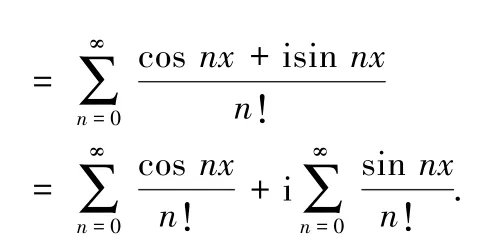
有 ez＝ eeix＝ ecosx＋isinx＝ ecosx·eisinx＝ ecosx［cos（sinx） ＋isin （sinx）］.

取x＝ π，得

3 结束语

求收敛的数项级数“和”是级数理论中的一个重点与难点，教学过程中因学时限制不能做系统地介绍，本文归纳和总结了一些典型的求“和”方法，主要涉及利用数项级数、幂级数、傅里叶级数及复级数的分析性质、和函数及函数的级数展开等对收敛的数项级数求“和”，有助于学生对级数理论的深入理解和提高.