矩阵环的幂级数弱McCoy子环
王文康
(西北民族大学 数学与计算机科学学院,甘肃 兰州 730124)
0 引言

文献[2]中的命题1.1指出,当n≥2时, 任意约化环R(没有非零幂零元的环)上的n×n阶矩阵环Mn(R)不是幂级数右弱McCoy环.我们给出任意环R的矩阵环Mn(R)的两个幂级数右McCoy子环和两个幂级数右弱McCoy子环,讨论reduced环与幂级数右弱McCoy环之间的关系.
用R表示数域F上的一个环.nil(R)表示环R中所有的幂零元做成的集合.Mn(R)表示环R上的n×n矩阵环,R[[x]]表示环R上的幂级数多项式环.
1 主要结果
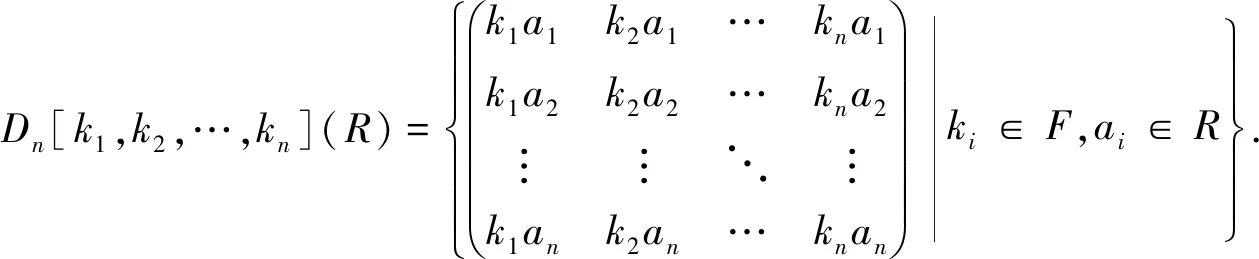
我们将(Dn[k1,k2,…,kn](R))[[x]]与Dn[k1,k2,…,kn]R([[x]])看作是相同的.
定理1 设R是一个环,那么Dn[k1,k2,…,kn](R)是幂级数右McCoy环,从而是幂级数右弱McCoy环,其中n≥2.
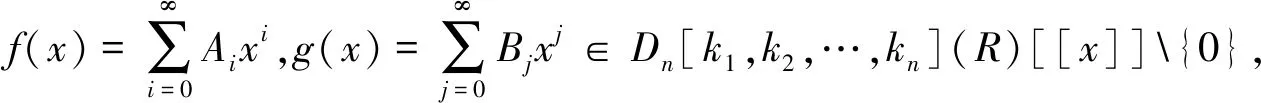

其中as(i),bs(j)∈R,0≤i,j<∞,1≤s≤n.
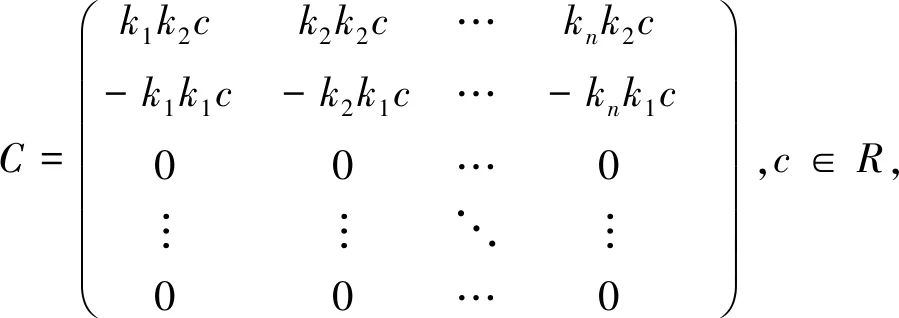

其中0≤i<∞.
那么Dn[k1,k2,…,kn](R)是幂级数右 McCoy 环,从而是幂级数右弱 McCoy 环,其中n≥2.

推论1 设R是一个环,那么Dn(R)是幂级数右McCoy 环,从而是幂级数右弱 McCoy 环,其中n≥2.
一个环R称为 reduced,如果它没有非零的幂零元, reduced环又被称为约化环. 由文献[2]的命题1.2可得reduced环是幂级数右弱 McCoy 环.下面说明反之则不成立.
命题1 幂级数右弱 McCoy 环不是reduced环.
证明由推论1,D2(R)是一个幂级数右弱McCoy环.
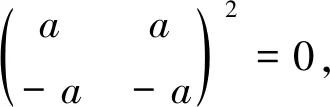

采用与定理1类似的方法可得
定理2 设R是一个环,那么DnT[k1,k2,…,kn](R)是幂级数左 McCoy环,从而是幂级数左弱 McCoy 环,其中n≥2.

CBj∈nil(DnT[k1,k2,…,kn](R)),其中0≤i<∞.
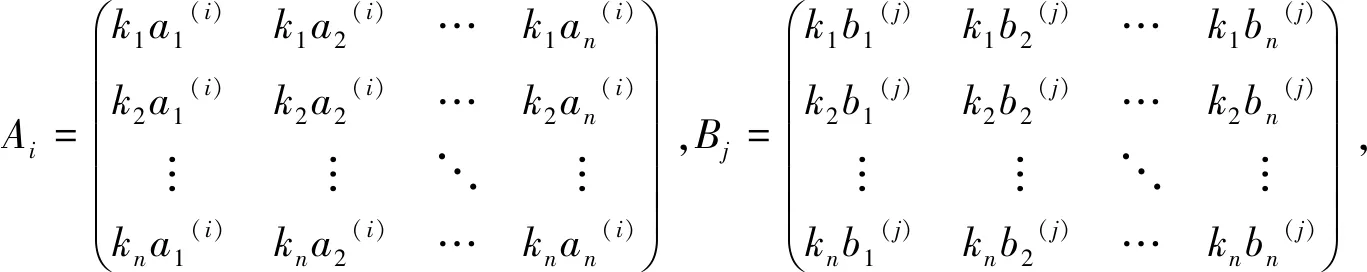
其中as(i),bs(j)∈R,0≤i,j<∞,1≤s≤n.
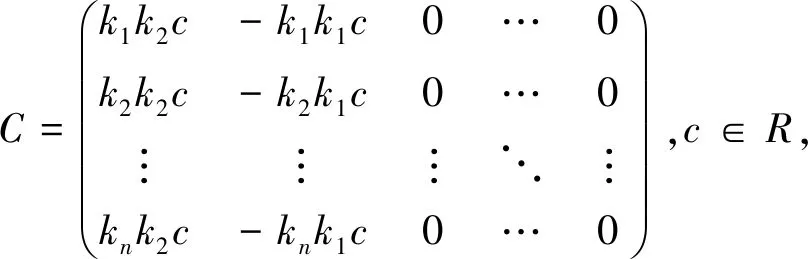

其中0≤j<∞.那么DnT[k1,k2,…,kn](R)是幂级数左McCoy 环,从而是幂级数左弱 McCoy 环,其中n≥2.
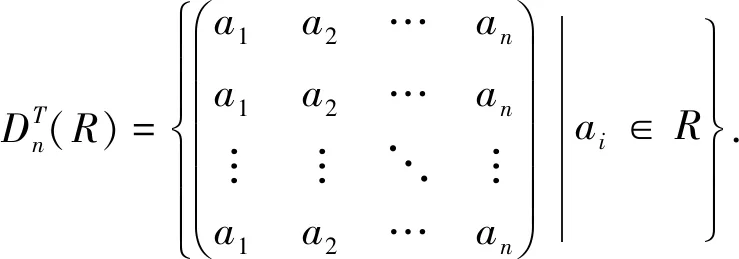
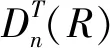
命题2 幂级数左弱 McCoy 环不是reduced环.
证明由推论2,D2T(R)是一个幂级数左弱 McCoy 环.


