具有加性噪声的Boussinesq方程的随机吸引子
富 娜,杨 墨
(西南交通大学 数学学院,四川 成都 610031)
0 引 言
设Ω是R3上带有光滑边界Γ的有界区域,我们考虑带有可加白噪声的Boussinesq方程:
(0.1)
其边界条件
u|Γ=Δu|Γ=0
(0.2)
给定初值条件
u(0)=u0,ut(0)=u1,
(0.3)
其中,随机函数W(t)是定义在概率空间(Ω,F,P)上的一维双边维纳过程,q(x)描述了一个可加白噪声.
假设(0.1)中非线性函数f(u)满足下面的条件
f∈C2(R,R),f(0)=0
(0.4)
|f″(s)|≤C(1+|s|p-2), 2≤p≤5
(0.5)
(0.6)
其中p>0,c>0是给定的常数,λ1是第一特征值.
自1872 年J.Boussinesq[3]推导出描述在浅水中小振幅长波传播的 Boussinesq方程以来 ,各种类型的Boussinesq方程就成为众多学者研究的对象.古典Boussinesq方程可描述为
utt-uxx-αuxxxx=β(u2)xx.
(0.7)
这里u(x,t)为流体自由表面的运动,常数α>0、β>0依赖于流体的深度和长波的特征速度. 当α<0时,方程(0.7)被称为“好”的Boussinesq 方程.Bona和Sachs[4]研究了“好”的Boussinesq方程的初值问题的局部解的适定性.Sachs[5]研究了方程(0.7) 的初值问题整体解的不存在性.当α>0时, 方程(0.7)被称为“坏”的Boussinesq 方程. 1982年, Deift等[6]将反散射理论应用于“坏”的Boussinesq方程的研究, 首次证明在初始函数呈负指数阶一致衰减的条件下,下面的Boussinesq方程的初值问题是可解的.
utt-uxx-3uxxxx=-12(u2)xx.
(0.8)
1985年Levine和Sleeman[7]进一步指出,在一定条件下,方程(0.8)的初边值问题不可能存在整体解.1996年陈国旺和杨志坚[8]用不同的方法讨论了更一般的“坏”的Boussinesq 方程的初边值问题解的“Blow up”问题.2008年,宋长明等[9]证明了一维情况下具强阻尼“坏”的Boussinesq 方程存在整体光滑解.2008年,杨志坚和郭柏灵[10]证明了多维Boussinesq 方程初值问题整体弱解的存在性. Lai等[11]研究了更一般的具阻尼Boussinesq 方程的Cauchy问题的整体适定性,并给出一个长时间的渐近解.
整体吸引子是研究具有耗散项非线性发展方程的长时间行为的一个基本概念,现已有很多研究[12-13]. Boussinesq方程的整体吸引子问题受到广泛关注[14-17].
2012年,杨志坚[18]研究了具阻尼项的Boussinesq方程
utt-Δut+Δ2u-Δf(u)=g(x)
解的长时间行为,在f(u)非超临界情况下得到方程对应解算子半群整体吸引子及指数吸引子的存在性. 现在我们有必要给上面的方程增添一个随机部分——加性白噪声, 来研究随机的情形, 它的整体吸引子是否仍然存在?
本文的安排如下:第一部分引言; 第二部分讨论了方程(0.1)初边值问题解的存在惟一性以及方程的解可以确定一个随机动力系统; 第三部分得到方程解的有界性; 第四部分证明随机吸引子的存在性.
1 解方程并产生相应的随机动力系统
为了本文证明方便,将空间L2(Ω)中的内积和范数记为(·,·)0和‖·‖0,并将其定义为
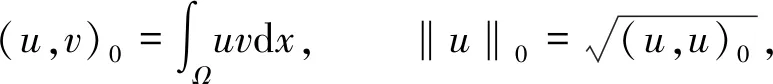
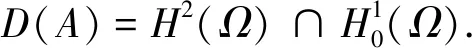

引入内积空间E=H×L2(Ω),将空间E中的内积和范数记为(·,·)E和‖·‖E,并将其定义为

其中u=(u1,u2)T,v=(v1,v2)T.
为了证明解的存在性,设v=ut,则方程(0.1)的初边值问题与下面的一阶发展方程问题等价
定义线性算子L∶D(L)⊂E→E,其中L的定义域为集合
令
则方程(1.1)与下面的系统等价
(1.2)
令ϑ=(u,z)T=(u,ut-qω)T,则通过保测度变换,可得出系统(1.2)的等价系统

(1.3)
为得到方程(1.2)的解的存在性,下面研究算子L的性质:
引理1.1 算子满足
(i) 对任意的ϑ∈D(L),有(L(ϑ),ϑ)E≥0.
(ii)I+L的值域为E,其中I为恒等算子.
(iii)-L的预解集包含R+=[0,+∞).
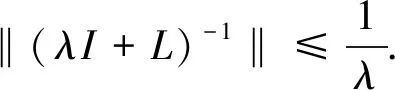

对λ≥0以及ϑ=(u,v)T∈D(L),有
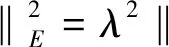
因此可知,‖(λI+L)ϑ‖E≥λ‖ϑ‖E,故可验证算子L满足性质(iv).
对于性质(ii)可参考文献[19-21].
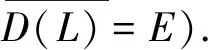
定理1.2 假设(0.4)~(0.6)成立,对任意ϑ0∈E,存在惟一的弱解ϑ∈C0([0,∞);E)满足
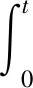
且对任意固定t≥0,映射
S(t)∶ϑ0=(u0,u1)T→ϑ(t)=(u(t),ut(t))T,E→E.
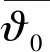
2 吸收集
这一部分将证明半群S(t)在E上存在有界吸收集,为了得到这一结论,将方程(0.1)的初边值问题转化为一阶方程.
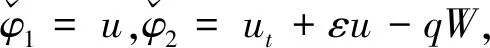
设
则问题(2.1)等价于
(2.2)
由方程(2.2)可知,其解可以定义一个连续的算子半群
且满足S(t)=RεSε(t),其中(u,ut)→(u,ut+εu)是E上的一个同构,所以Sε(t)是S(t)的一个同构.同时由于(1.2)与(1.3)的等价关系,我们只需要研究(1.2)的等价系统(2.2)的随机动力系统Sε(t).
下面介绍一个辅助引理,它是证明半群的吸引子的存在性的核心工具.

证明在E中
(2.3)
由Green第二公式以及零边界条件可得
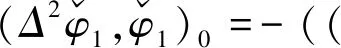
(2.4)
由式(2.3),式(2.4) 可得
因此有
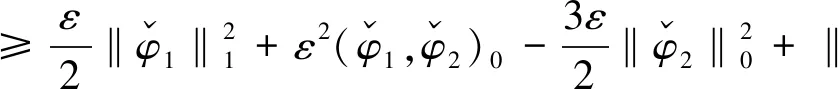
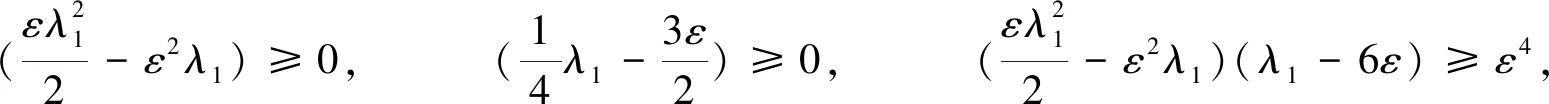
所以上式大于等于0,即引理2.1成立. 证毕.
为得到系统(2.2)的解的有界性,有:
引理2.2 若对E中任意一个有界集B,都存在一个缓增的随机变量C1(ω)>0和T0(ω)=T0(B,ω)∈B,对t≥T0(w)以及φ(0)∈B有‖Sε(t)φ(0)‖≤C1(ω).
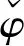
(2.5)
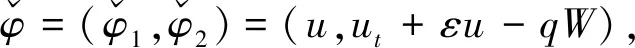
整理可得
利用Green第二公式可得
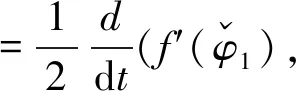
因此有
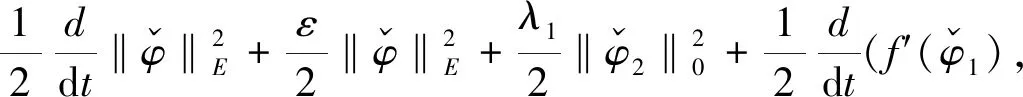
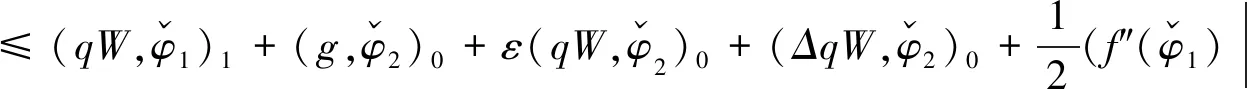
由式(0.5)和Holder不等式以及Young不等式可知,
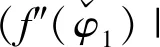
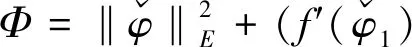
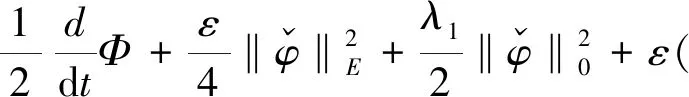
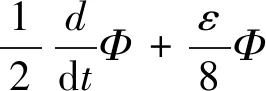
其中K为(0,λ1)之间的常数.
因此有
≤+C1(ε,k)(Φ+O(|g|)+H(|w|))P,
其中O(|g|),H(|W|)是关于|g|、|W|的正定函数.
令Ψ=Φ+O(|g|)+H(|W|),则可得
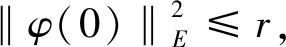
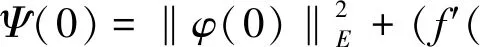
(f′(u)u,u)0≥-k‖
由一般Gronwall公式[12]以及Sobolev嵌入定理有
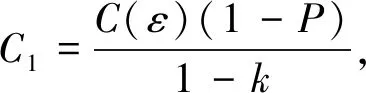

3 渐近紧性
为了得到系统(0.1)的初边值问题,在E中存在吸引子,我们下面证明Sε(t)的渐近紧性.换而言之,Sε(t)具有紧的吸收集,因此需要将式(0.1)的初边值问题的解分为两部分.
设u=w+v,其中w,v分别是下面问题的解,则式(0.1)可分解为
和
设
于是式(3.1)可以转化为下面的方程
(3.3)
引理3.1 对E中的任意有界集B,有
证明对等式(3.3)两边与φb在E中作內积,有
(3.4)
而
因为
所以
(3.5)
于是,由式(3.4)可得
由Gronwall引理可得
证毕.
设
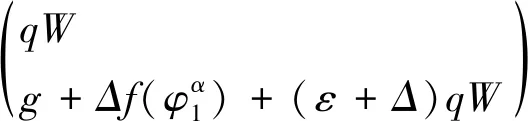
于是式(3.2)可写作如下形式
(3.6)
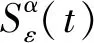
引理3.2 设B0是空间E中的任意一个吸收集,存在一个正常数C2,使得
其中σ∈(0,1].
证明用Aσφα对式(3.6)两边在E中作內积,得
(3.7)
用类似于引理2.1的方法计算可得
于是,有
根据Cauchy-Schwartz不等式,
(3.8)
(3.9)
(3.10)
(3.11)
下面首先说明引理证明过程中用到的Sobolev嵌入定理.
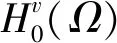
其中v∈[1,2].
本文讨论n=3时的情况.当n=3时,有H2(Ω)⊂L∞(Ω),L4(Ω)⊂H1(Ω),取v=σ+1,所以有
以及
由Sobolev嵌入定理可得
≤M1.
再利用Gronwall不等式,计算可得
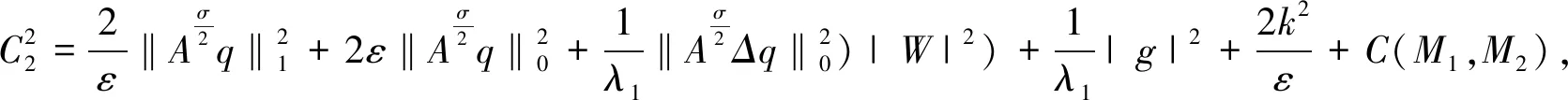
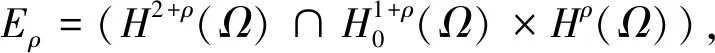
定理3.3 随机动力系统Sε(t)在E中有一个紧的随机吸引子A,其中A是B0的ω-极限集.
证明由于随机动力系统S(t)与随机动力系统Sε(t)是等价的,则随机动力系统Sε(t)存在一个紧的随机吸引子Aε.

