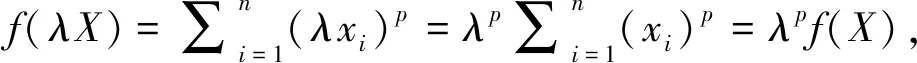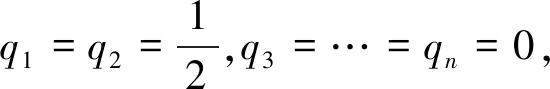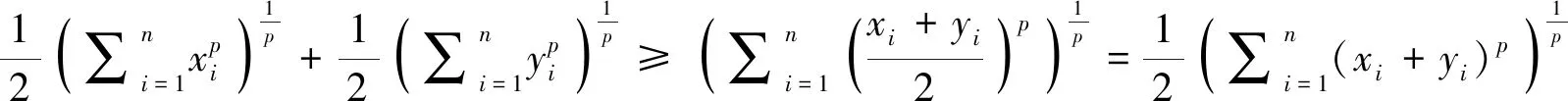推广加权型Jensen不等式

关却东智 ，索南仁欠,2

(1.青海师范大学 数学与统计学院，青海 西宁 810008；2.青海师范大学 研究生院，青海 西宁 810008)

0 引言

凸函数是数学中广泛使用的重要概念之一，例如与几何测度论，极值问题与凸规划的理论，数学物理方程，边界结构等都具有密切的联系.经凸理论研究者发现,在不等式的证明中凸性是常用的工具.而Jensen不等式是关于描述凸函数性质的不等式，它与凸函数的定义息息相关，是凸函数几何意义的另一种表达形式.

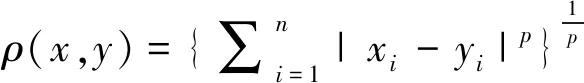
本文应用构造方法刻画化归思想，使其在复杂问题等价转化中起到了一定的指导作用.

1 预备知识

1)凸集定义：若f(X)在I⊂R上有定义，对于x,y∈I和t>0，都存在tx+(1-t)y∈I，则称I为凸集.

2)凸函数定义：设f(X)在非空凸集I上有定义，若∀x,y∈I,t>0，有f(tx+(1-t)y)≤tf(x)+(1-t)f(y)，则称f(X)在I上是凸函数；不等号相反时为凹函数.

3)p阶齐次函数定义：设p为正整数，若对于任意(x1,x2,…，xn)=X∈Rn和λ>0，都有

f(λX)=f(λx1,λx2,…,λxn)=λpf(x1,x2,…,xn)=λpf(X)，

则f(x)为Rn上的p阶齐次函数.

4)Taylor定理：若n元函数f(x)在点(x'1，x'2，…,x'n)的领域U存在n阶连续的偏导数，则有

同理，可以利用方阵将n元函数Taylor展开式转化成Hesse矩阵形式：

令X=(x1，x2，…,xn)，X'=(x'1，x'2，…,x'n)，ΔX=(Δx1，Δx2，…，Δxn)T，则有f(X)=f(X')+其中︳X',AT表示矩阵A的转置矩阵.

为f(X)点X'处的Hesse矩阵.

5)正定阵判别法：实二次型q(x1，x2，…,xn)=XTAX,X=(x1,x2，…，xn)是正定(半正定)的充分必要条件，是一切主子式(行列下标相同的子式)都大于零.

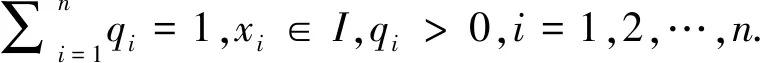
f(q1x1+q2x2+…+qnxn)≤q1f(x1)+q2f(x2)+…+qnf(xn)，此不等式称为一元函数加权Jensen不等式.

利用Jensen定理证明方法将一元函数Jensen不等式推广到多元函数Jensen不等式.多元函数Jensen不等式对解决级数等问题时具有独特的作用，只要这样，级数在等价函数下是凸的，则可以通过预备知识与下面的引理1、引理2解决，以泛函分析著名Minkouski不等式为例.

2 Jensen不等式推广与齐次函数性质

引理1 设n元函数f(X)在点X'=(x'1，x'2,…,x'n)的U(X')内存在二阶连续偏导数，若H(X)在X'为正定阵时，f(X)在X'处为凸函数.

证明H(X)≥0时由Taylor定理知，令

两边同时乘qi有

qif(x1i,x2i，…，xni)≥qif(X')+qif(X')T(x1i-x'1,x2i-x'2，…，xni-x'n)

再取和得

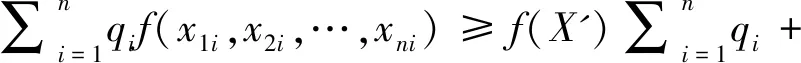
(1.1)

因此，f(X)在(X')处为凸函数.而(1.1)不等式称为凸函数Jensen不等式的推广.

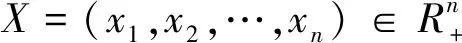
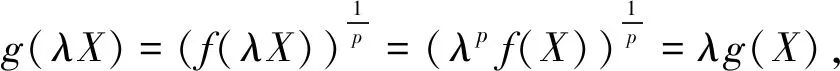
下证g(X)是凸函数，令q1+q2=1，因f(X)为凸函数，有

(2.1)

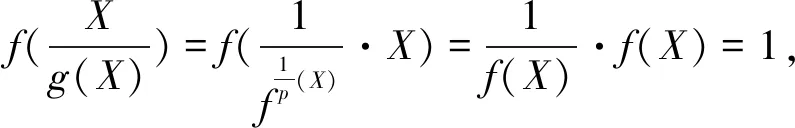
(2.2)

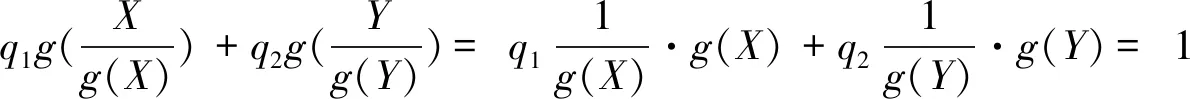
(2.3)

3 Minkouski定理证明

若xi,yi≥0，i=1,2,…,n，当p>1时，有

(3.1)