类比出新意——由倒序相加想到倒序相乘

刘 高

(甘肃省武威第六中学 733000)

《普通高中数学课程标准》(实验)把培养学生的类比推理能力作为培养目标之一.近几年全国各省市出现了类比思维的问题，这是一些思路开阔，情景新颖的创新题型，它们往往以问题为中心，不拘泥于具体的知识点，将数学知识，方法和原理融为一体，突出对数学思想方法的考查，体现数学的思维价值.在数学教学中，通过类比推理可寻求解决问题的方法和途径，从而培养学生的发散思维及合情推理的能力.

在数列一章的学习中类比的思想贯穿于其中.例如等差数列和等比数列无论是通项公式还是其它性质都有许多类似的特点.在学习的时候只要我们认真研究其特征，灵活应用，就一定能推陈出新.如由“倒序相加”联想到“倒序相乘”使得问题顺利解决就是一种常见的类比方法，现分析如下:

命题1若数列{an}为等差数列，Sn是其前n和，则有，

S2n=n(a1+a2n)=n(a2+a2n-1)=…=n(an+an+1) ①，

S2n-1=(2n-1)an②.

对于②式有以下两种推导方法：

证明(法一)S2n-1=a1+a2+a3+…+an+…+a2n-3+a2n-2+a2n-1.

如上所示a1和a2n-1相结合,a2和a2n-2相结合等等,这样共有n-1对结合，之后还余中间项an.而每对结合都等于2an即：

a1+a2n-1=a2+a2n-2=…=an-1+an+1=2an,

所以有S2n-1=(2n-1)an.

但这种解法对一部分学生来说还有困难，若采用下列推导法就会使问题变的容易理解.

(法二)(倒序相加)

S2n-1=a1+a2+a3+…+an+…+a2n-3+a2n-2+a2n-1①,

S2n-1=a2n-1+a2n-2+a2n-3+…+an+…+a3+a2+a1②.

由①+②得2S2n-1=2(2n-1)an,所以S2n-1=(2n-1)an.

通过类比可得到如下结论：

命题2 若数列{bn}为正项等比数列，Tn是其前n项积，则有T2n-1=(bn)2n-1.(类似于性质1中的②式)

证明(倒序相乘)

T2n-1=b1·b2·b3·…·bn·…·b2n-3·b2n-2·b2n-1①,

T2n-1=b2n-1·b2n-2·b2n-3·…·bn·…·b3·b2·b1②.

由①×②得(T2n-1)2=(bn)2(2n-1),

所以T2n-1=(bn)2n-1.

反思求Tn时若不知n的奇偶性就需讨论n为奇数和n为偶数两种情况来求解，如果采用倒序相乘就避免讨论.

举例如下：

Sn为数列{an}前n项的和，求Sn.

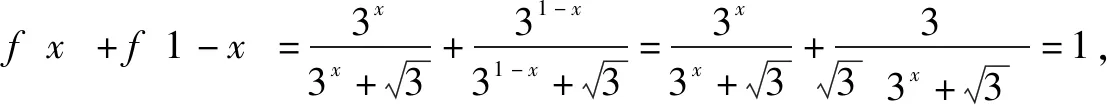
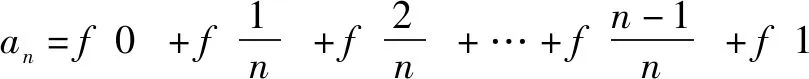
由①②得2an=n+1,

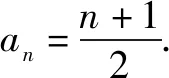
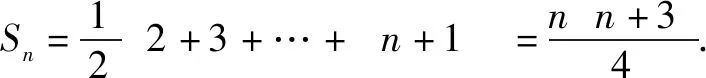
例2已知等比数列{an}满足an>0(n=1,2,…)且a5·a2n-5=22n(n≥3)，则当n≥1时求 log2a1+log2a3+…+log2a2n-1的值.

解log2a1+log2a3+…+log2a2n-1=log2(a1·a3·…·a2n-1).

令Tn=a1·a3·…·a2n-1①,

Tn=a2n-1·a2n-3·…·a1②,

由①×② 得(Tn)2=(a1·a2n-1)·(a3·a2n-3)·…·(a2n-1·a1)=(a5·a2n-5)n=(22n)n,

∴Tn=2n2.则log2a1+log2a3+…+log2a2n-1=log2Tn=log22n2=n2.

反思由例1的“倒序相加”类比出例2的“倒序相乘”使得问题得以顺利解决.

类比是一种很重要的科学方法.在平时教学中只要肯东脑筋不断对旧知识进行类比探究，推陈出新，我们的教学就一定会收到事半功倍的效果.