一类ka+b型几何最值题的研讨与拓展

广东省广州市广州中学

1 问题提出

已知ΔABC中,BC=a,AC=b,AB=c,a2+b2=c2=25,试求2a+b的最大值.

2 解法研讨

显然,可以画出一个圆O,如图1,AB是⊙O的直径,原题等价于求2BC+AC的最大值;下面先研究它的几种解法.

解法一:设

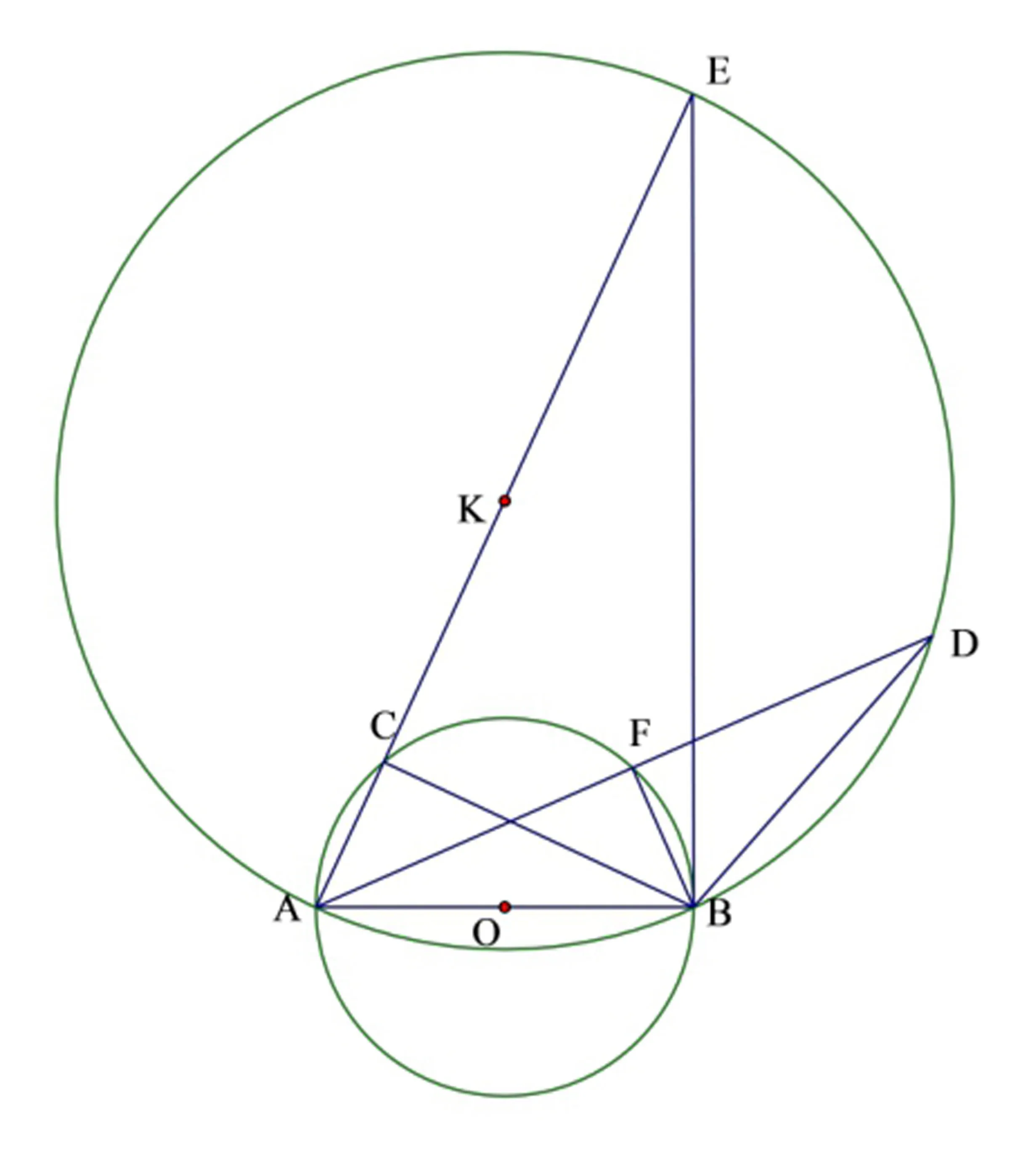
图2

解法二:如图2,点F在半圆O上运动,m=2FB+AF,延长AF至点D,使得FD=2FB,连接BD,设∠ADB=∠α,由∠AFB=∠BFD=90°有再作

记⊙K的半径为r,由于⊙K是一个定圆,AD是⊙K的动弦,∴当AD与直径AE重合时,m=AD=AE,取到最大值,由勾股定理可得,最大.

解法三:设∠ABC=β,a=5 cosβ,b=5 sinβ

图3

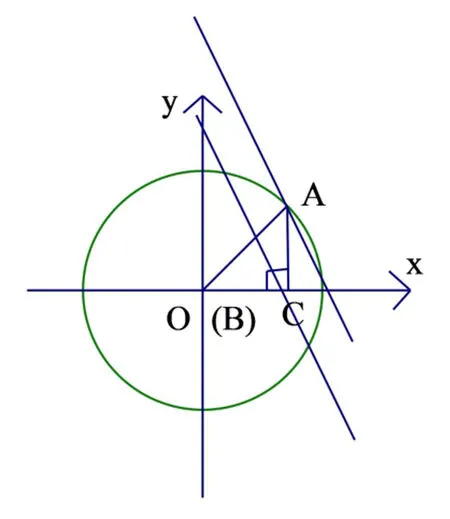
图4

解法四:如图3,以点B为坐标原点,点B与点O重合,直线BC为x轴建立直角坐标系,以O为圆心,,OA为半径作圆,则OC=x=a,AC=y=b,有

以上四种解法,分别是从判别式、纯几何推导、三角函数、解析法几方面思考得来的方法,本题还可以推广求得ka+b的最大值.

3 变式与拓展

3.1 变式问题

变式题一已知ΔABC中,BC=a,AC=b,AB=c,a2+b2=c2=25,试求3a+b的最大值;

根据圆具有对称性,a+2b、a+kb与2a+b、ka+b问题属于等价变形问题,所以不予讨论;显然,与解法二类似,可以求得,最大;

变式题二已知ΔABC中,BC=a,AC=b,AB=c,a2+b2-ab=c2=25,试求2a+b的最大值;

分析与解:如图5,点F在圆O上运动,m=2FB+AF,延长AF至点D,使得FD=2FB,连接BD,设∠ADB=α(下同),由∠AFB=60°,∠BFD=120°,记∠FBD=β(下同),则α+β=60°,又即sinβ=2 sinα,故α是一个定值.

图5

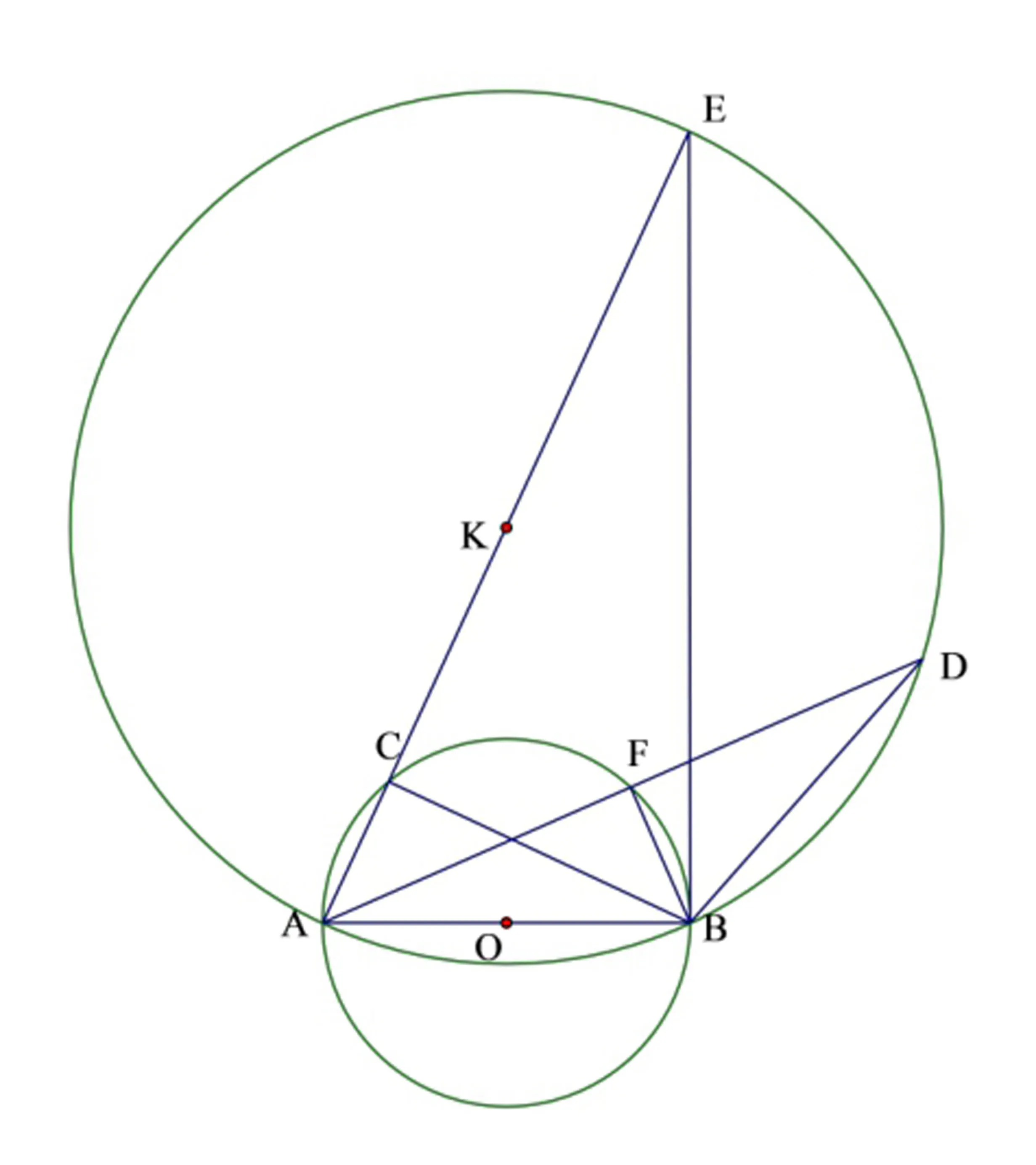
图6

再作ΔABD的外接圆⊙K,记⊙K的半径为r,易证得m等于圆K中过点A的任意弦长,

∴m=2r最大,由

3.2 拓展推广问题

推广题1已知ΔABC中,BC=a,AC=b,AB=c,a2+b2=c2=25,试求ka+b的最大值(k为正整数);显然,当k=1时,是一个常态问题,不再赘叙.

当k＞2时,如图6,当BC=kAC时,点C为所求的位置,此时,m取到最大值;再延长AC至点E,CE=CB,连接EB,作ΔEAB的外接圆⊙K,由∠ECB=∠BCA=90°,知ΔECB∽ΔBCA,可得,∠ABE=90°,AE为⊙K的直径,延长AF交⊙K于点D,连接BD,易证ΔDFB∽ΔECB,DF=kFB,m=kFB+AF=DF+AF=AF,显然,由直径不小于弦,可得AE≥AD,m=AE时最大.

由AB=5,可得,当最大.

推广题2已知ΔABC中,BC=a,AC=b,AB=c,a2+b2-2abcosC=c2,∠C=θ为锐角,c和θ为常数,试求ka+b的最大值(k为正整数常数);