抓住数学本质提升学生数学素养

广东省广州市番禺中学

1 数学本质的意义

《普通高中数学课程标准》(2017年版)提到:数学是研究数量关系和空间形式的一门科学.数学本质就是提升学生的数学素养,引导学生会用数学眼光观察世界,会用数学思维思考世界,会用数学语言表达世界.为此,突出数学本质教学,就是要求我们教师在教学过程中,让学生理解数学概念,把握数学思想,感悟数学特有的思维方式.

2 数学本质的教学意义

新课标在其十大基本理念中指出:“高中数学课程应该返璞归真,努力揭示数学概念、法则、结论的发展过程和本质.通过典型例子的分析和学生自主探究活动,使学生理解数学概念、结论逐步形成的过程,体会蕴含在其中的思想方法,追寻数学发展的历史足迹,把数学的学术形态转化为学生易于接受的教育形态.”虽然这不能完全揭示数学教学的本质,但是它为我们普通高中数学教师提供了一种在平时教学实践中抓住教学本质的努力方向.

我们的教学不但要使学生达到知识与方法的融会贯通,而且要把数学的思想方法、本质规律以及内部联系等“灵魂”性的东西揭示出来,并内化给学生,使他们形成能力,为他们的终身发展打下基础.

3 数学教学注重数学本质例谈

下面通过具体例子来展示抓住数学本质进行数学教学的重要性.

3.1 抓住数学本质在概率统计教学中的应用

例1.从一群游戏的小孩中随机抽出k人,一人分一个苹果,让他们返回继续游戏.过了一会儿,再从中任取m人,发现其中有n个小孩曾分过苹果,估计参加游戏的小孩的人数为( )

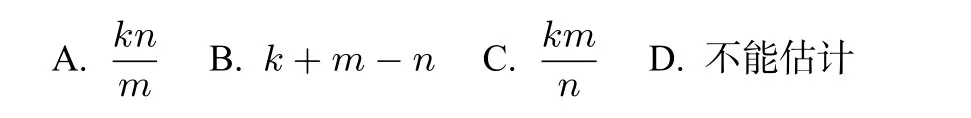
解答该题,一定要跟学生揭示此类题目的数学本质——抽样调查、概率统计,用样本估计总体.

解答:设参加游戏的小孩有x人,则即参加游戏的小孩的人数为人.选C.

理解了数学本质,就可以举一反三,攻克这一类题目.

变式1:池塘里有一群鱼,现想知道池塘里鱼的数量大概是多少.怎么解决?

理解数学本质,抓住数学本质,可以类比上面统计小孩的人数来解答本题.

解答:从池塘里捞起k条鱼(抽样调查),在这些鱼身上做上一些不会被水冲掉的记号,然后把这些鱼又放回池塘里(相当于均匀搅拌).过一段时间,再重新从池塘里捞起m条鱼,记录身上有做过记号的鱼的数目为n条,便可由样本估计总体.同样,设池塘里的鱼总共有x条,则即池塘里鱼的数量为条.

3.2 抓住数学本质在解析几何数形结合教学中的应用

解析几何的数学本质——数形结合.教学过程中,要跟学生充分展示这一点.

例2.已知x、y使方程x2+y2-2x-4y+4=0,则的最小值是( )

分析:此类问题的本质是直线的截距问题.(x,y)点既在直线上,也在圆上,只有当直线与圆相切时,直线截距才有最大或者最小值.

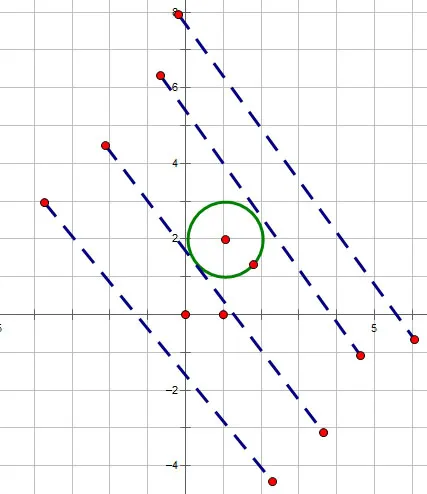
图1

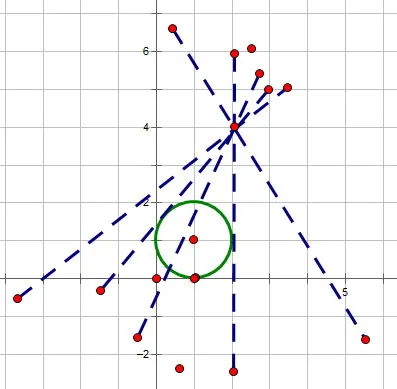
图2

例3.若实数x,y满足x2+y2-2x-2y+1=0,则的取值范围为

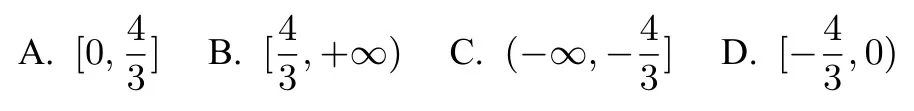
例4.直线y=x+b与曲线有且只有一个交点,则b的取值范围是( )

分析:解答本题,同样,要抓住该题数形结合的数学本质.

解答:由题意可知,曲线方程表示一个在y轴右边的单位圆的一半,则圆心坐标为(0,0),圆的半径r=1,画出相应的图形,如图3所示:∵当直线y=x+b过(0,-1)时,把(0,-1)代入直线方程得:b=-1;当直线y=x+b过(0,1)时,把(0,1)代入直线方程得:b=1;∴当-1＜b≤1时,直线y=x+b与半圆只有一个交点.又直线y=x+b与半圆相切时,圆心到直线的距离d=r,即解得(舍去)或直线与曲线只有一个交点时,b的取值范围为-1＜b≤1或

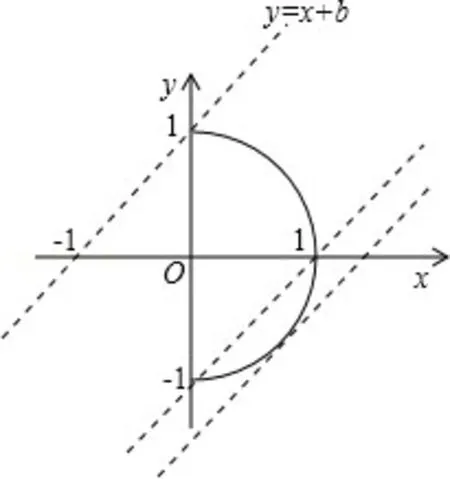
图3

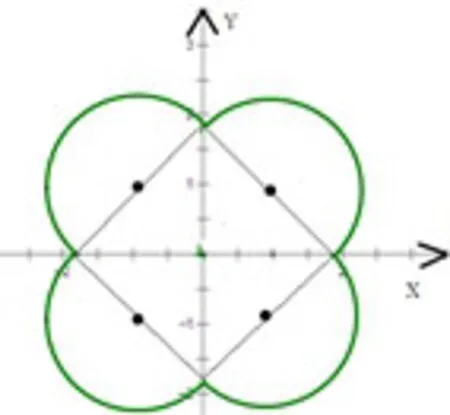
图4

例5.由曲线x2+y2=2|x|+2|y|围成的图形的面积为( )

A.8+2πB.8+4πC.6+4πD.6+2π

分析:同样,要抓住该题数形结合的数学本质.

解答:由题意画出曲线对应的图形(如图4所示).当x＞0,y＞0时,曲线的方程为(x-1)2+(y-1)2=2.由曲线关于原点对称可知,此曲线所围成的图形由一个边长为的正方形与四个半径为的半圆围成.因此围成的图形的面积为选B.

由以上实例,我们看到,数学教学要注重数学本质的揭示,这是数学教学的立足之本.我们数学教师要善于抓住数学的本质,促进学生的数学理解,培养学生的理性思维,提高学生学习数学的兴趣.只有这样,才能引领学生在数学学习的过程中,不断开拓数学思维,提升学生的数学素养,让学生真正体会学数学、用数学.